钢带式轮胎试验台气轴承支撑装置性能分析及优化
2019-09-10王飞飞张越男卞学良
王飞飞 张越男 卞学良







摘要 针对钢带式轮胎试验台中钢带支撑刚度对道路试验结果的影响,设计一种气轴承支撑装置,并基于CFD数值仿真和正交试验,研究输入孔径、输入压强、钢带速度、楔形角度对轮胎试验台气轴承支撑装置承载压力的影响。仿真分析了承载压力随各个影响因子的变化规律,其结果显示钢带速度和楔形角度对承载压力影响较小,输入孔径和输入压力是承载压力的主要影响因素。在各个影响因子变化规律基础上,基于正交试验优化方法,以最小输入压强为目标函数,得到最优的支撑件结构。
关 键 词 钢带式轮胎试验台;气轴承支撑装置;CFD数值仿真;承载压力;正交试验
中图分类号 TH117 文献标志码 A
Simulation of the air bearing suspension support characteristics and optimization of suspension belt type tire test rig
WANG Feifei, ZHANG Yuenan, BIAN Xueliang
(School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China)
Abstract Air bearing suspension support characteristics of suspension belt type road simulator are established. The model is simulated using FLUENT solver and orthogonal test. The load pressure′s effects of feed hole diameter, feed pressure, steel belt speed and the angle of the wedge gap on the suspension support characteristics on the dynamic lubricating characteristic parameters are analyzed. It shows that feed hole diameter and high feed pressure increases the load pressure while the fluid bearing pressure changes with different influence factors. The sensitivity that various factors affect the fluid bearing pressure is analyzed by doing the orthogonal test. The optimal supporting structure is obtained by the minimum feed pressure target function.
Key words suspension belt type road simulator; air bearing suspension support characteristics; CFD numerical
simulation; load pressure; orthogonal test
0 引言
室內道路模拟试验不仅避免了外界雨雪等恶劣天气的影响,而且缩短了试验时间和研发周期,较其他试验方法突显了它超强的适应性,因此,要完成汽车整车或零部件的测试,轮胎试验台成为汽车必不可少的道路试验设备[1-2]。传统的平台式轮胎试验台运行速度较低,转鼓式的试验结果受转鼓曲率的限制,目前,钢带式轮胎试验台成为轮胎试验的主要实验装置。
钢带式轮胎试验台采用双滚筒张紧钢带结构组成试验台架,通过改变钢带表面材料的粗糙度模拟车轮在不同种路面上的行驶工况,避免了实验结果受转鼓半径影响的弊端。由于轮胎的橡胶材料较软,在轮胎垂直载荷下胎面和钢带的变形不可忽略,而钢带的变形反过来影响对轮胎的支撑压力分布,因此,研究钢带的支撑刚度具有重要意义。
国际方面,各科研机构通过水、气轴承支撑钢带来平衡钢带上方轮胎的垂直载荷[3],提高钢带的支撑刚度。美国MTS的Flat-Trac[4-5]、TMSI的On LEVELTMTire Test Machine、西班牙Malaga University[6]、德国Karlsruhe University[7] 等公司研制的轮胎试验台采用水轴承支撑;美国Calspan[8]、日本A&D、德国TS等公司的轮胎试验台采用气轴承支撑,而这些模拟器水、气轴承采用的大多是静压止推轴承形成水膜或气膜的机理。国内方面,吉林大学首次把轮胎的动力滑水机理应用在道路模拟试验台上[9],通过数值迭代计算方法,仿真出高速轮胎实现完全水滑的更低轮胎速度。
本文将动压气膜原理应用到钢带式轮胎试验台气轴承支撑装置中,充分考虑支撑装置各个参数对支撑压力的影响,研究各个参数的最佳匹配优化问题。基于CFD数值仿真分析方法,首先对各个影响因素进行了仿真分析,研究输入孔径、输入压强、钢带速度、楔形角度的变化规律,为正交试验[10]因素水平范围的合理设定提供理论依据,然后根据各个因素的仿真实验规律设计正交试验,找到以最小输入压强为目标的最佳支撑件结构参数,并对实验结果进行极差分析,得到对实验结果影响最大的影响因子,并确定各影响因子对承载压力影响的主次顺序。
1 模型的建立
1.1 轴承支撑装置结构参数
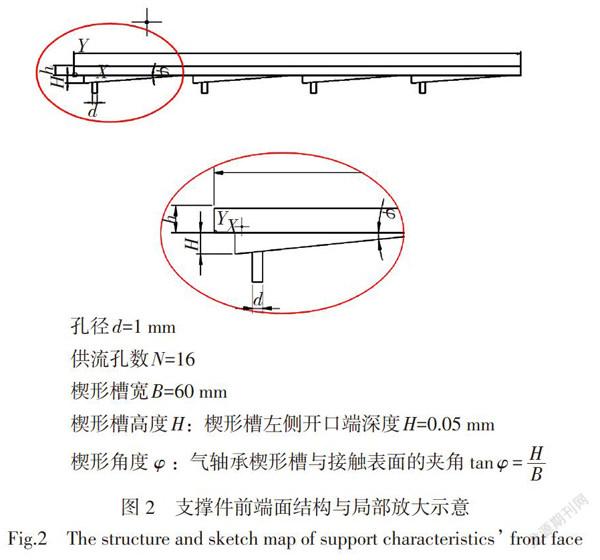
图1、图2分别为气轴承支撑装置上表面和前端面结构示意, 支撑件上表面整体长度为270 mm,宽度为300 mm,相邻两个斜槽的间距为6 mm;4个输入孔均匀分布在楔形槽的左侧。
[φ]
1.2 流体模型假设
流体在间隙中进行复杂的三维流动,为了便于楔形槽中气膜的仿真计算,现对其做出以下假设[11]:
1)楔形槽中的流体与接触的固件之间既没有热量交换,也没有相对滑动,流体的流动是一个等温过程;
2)由于钢带张紧力较大导致的钢带变形;
3)流体的流动状态为层流,定常态;
4)支撑流体为牛顿流体,求解时不涉及流体的质量。
1.3 网格划分
图3分别为气膜的主视图和在Gambit环境下建立的网格模型。气体模型的平面气体厚度相对于斜槽流体和圆柱流体的高度较小,圆柱孔的横截面积比平面气体小得多,圧力气体流经时,速度和压力变化很大,为保证计算的稳定性和准确性,在网格划分时进行了分区和局部细化。
沿钢带运动方向的长度a=270 mm,纵向宽度b=300 mm,钢带平面和支撑件上端面之间流体膜的厚度为t=0.03 mm。采用六面体网格,间隔尺寸取0.2,由于钢带与支撑件上端面的相对速度比较大,所以在流体膜的厚度上对流体进行三层划分,整个流体模型的网格数量约90万个,检查网格的质量,保证网格扭曲度符合要求、没有负体积网格。
基于计算流体力学软件Fluent,对支撑装置进行流体动力学仿真分析。该分析采用层流计算模型,流体材料选择空气,圆柱流体模型的底面为入口,平面流体模型与大气接触的四个侧面为出口,分别为压力入口和压力出口边界条件,将气膜与钢带接触的上表面设置为动边界,沿楔形槽收敛的方向平动,平动的速度为35 m/s。
2 控制方程
处于稳态工况下在气轴承支撑装置,气膜在轴承间隙区域内的流动属于三维定长不可压层流,在利用Fluent模擬气膜承载力分布时,满足的计算流体力学控制方程有质量守恒方程、动量守恒方程、能量守恒方程[12-16]。
2.1 质量守恒方程
连续性方程(连续性方程是质量守恒定律在流体力学中的表现形式)在直角坐标系下表现为
[∂ρ∂t+∂(ρvx)∂x+∂(ρvy)∂y+∂(ρvz)∂z=0], (1)
式中:vx,vy,vz为速度矢量在x,y和z方向分量;t是时间;ρ是密度。
2.2 动量守恒方程
流体为牛顿流体,并假设空气粘度不随温度变化而变化,粘度为定值的不可压缩流体动量方程为
[ρ∂u∂t=ρFx-∂p∂x+∂∂xμ∂u∂x+∂∂yμ∂u∂y+∂∂zμ∂u∂z+∂∂xμ3∂u∂x+∂v∂y+∂w∂z , ]
[ρdvdt=ρFy-∂p∂y+∂∂xμ∂u∂x+∂∂yμ∂u∂y+∂∂zμ∂u∂z+∂∂yμ3∂u∂x+∂v∂y+∂w∂z , ]
[ρdwdt=ρFz-∂p∂z+∂∂xμ∂u∂x+∂∂yμ∂u∂y+∂∂zμ∂u∂z+∂∂zμ3∂u∂x+∂v∂y+∂w∂z , ]
式中:P为流体微元上承受的压力;μ为流体的粘度;ρ为流体的密度;u、v、w分别是速度在x、y、z上的矢量。
2.3 能量守恒方程
流体的能量方程:
[∂(ρt)∂t+∂(ρTu)∂x+∂(ρTv)∂y+∂(ρTw)∂z=∂∂xKCP∂T∂x+∂∂yKCP∂T∂y+∂∂zKCP∂T∂z+ST], (3)
式中:T为流体的温度;K为流体的传热系数;ST为流体的粘性耗散项;ρ为流体密度;CP为流体的比热容。
3 支撑装置支撑特性的变化规律
基于流体的动压形成原理 ,对影响悬浮带式轮胎试验台支撑件和钢带接触面之间楔形槽中气膜动压支撑特性的,包括空气的输入压强P、钢带的速度V、楔形槽中流体的输入孔径d以及楔形槽角度等因素做一个系统的仿真,研究气膜的承载压力随各个影响因子的变化规律,以便对支撑结构进行优化设计。
3.1 承载压力随输入压强的变化规律
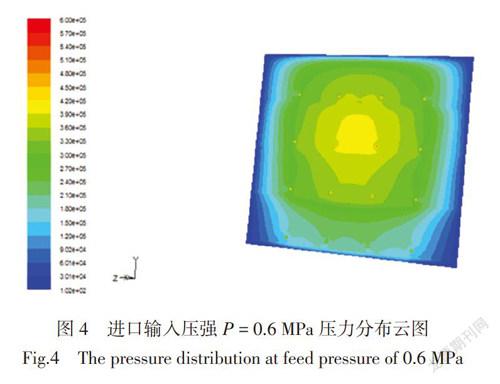
输入压强P的大小是影响气膜承载压力的重要因素,为了研究气膜承载压力随楔形槽中空气输入压强的变化规律,现保持气膜的结构模型不变,钢带传输速度恒为35 m/s,改变楔形槽中每流体的动压支撑特性仿真分析。如图4为压强P=0.6 MPa时的压力分布云图。
分析结果显示,在变压强条件下,气膜的压力云图的分布形式基本保持一致,在整个支撑平面上沿着钢带运动的方向关于支撑面的中心线轴对称,且中间区域压力大,四周压力逐渐变小,随着输入压强的增大,输入孔处压力过大,造成局部承载压力过大,反而不易于钢带的稳定。
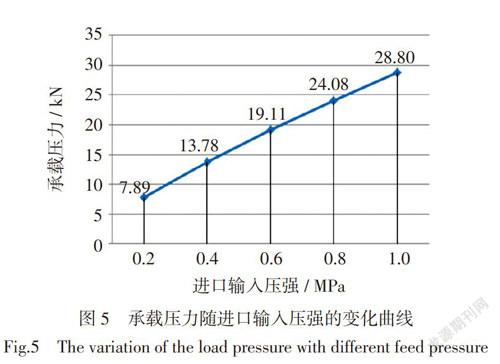
在Fluent软件中对支撑钢带的气膜上表面求压力积分,得到气膜的承载压力随楔形槽进口输入压强变化曲线图(图5)。
如图5所示:在其他外界条件不变时,气膜的承载压力随进口输入压强的增大呈线性上升趋势;输入孔的流量也随进口输入压强的增大而线性增大。当压强为1 MPa时,流体的进口流量最大,此时出口的泄漏速度也最快,为了保证流体支撑的稳定性,在输入压强不断增大时,必须不断的增大进口的输入流量。通过上述分析可见,承载压力数值浮动范围为20 kN,这说明输入压强对承载压力的影响极为显著。
3.2 承载压力随钢带速度的变化规律
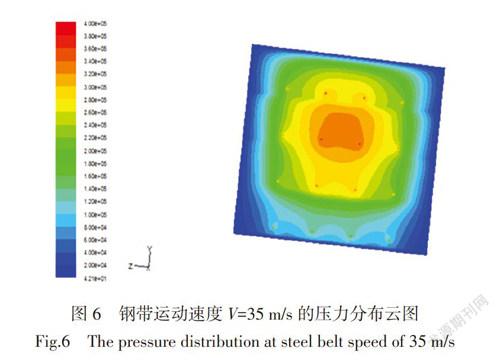
为了研究气膜对钢带的承载压力随钢带运动速度之间的关系,现保持所建的气膜模型结构不变,楔形槽进口输入压强恒为0.4 MPa,改变钢带的传动速度V。进行Fluent仿真分析,得到气膜上支撑面的压力分布云图(如图6)。
结果表明:随着钢带速度的不断增大,气膜承载压力在2.1 bar的区域不断增大,对钢带形成的悬浮支撑稳定性越来越高。
通过Fluent进行气膜的动力学计算,对支撑钢带的气膜上表面进行压力积分得到承载压力随钢带传动的变化曲线(图7)。
如图7所示:在其他外界条件不变时,气膜的承载压力随钢带速度的增大基本保持线性增大,但钢带速度对气膜承载压力不甚敏感,从钢带开始转动到以最大速度65 m/s进行运转,承载压力差值仅有0.78 kN。
通过Fluent对流体进口流量求解积分,得到楔形槽中空气输入流量基本保持在0.17 m3/min左右,这表明在汽车正常运行速度之内,钢带速度大小的变化不会导致系统的输入流量发生较大变化,流体的输入和流出能够达到一个稳定的平衡状态,从而间接表明楔形流体能够形成一个稳定的润滑和支撑系统,满足道路模拟试验的需要。
3.3 承载压力随输入孔径的变化规律
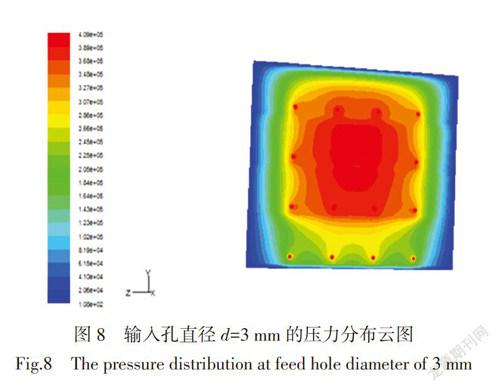
为了研究气膜的承载压力随楔形槽中流体输入孔直径的变化规律,现改变气膜模型中输入孔的直径d的大小,设置楔形槽中进口的输入压强为0.4 MPa,钢带速度恒为35 m/s,得到气膜上支撑面的压力分布云图(图8)。
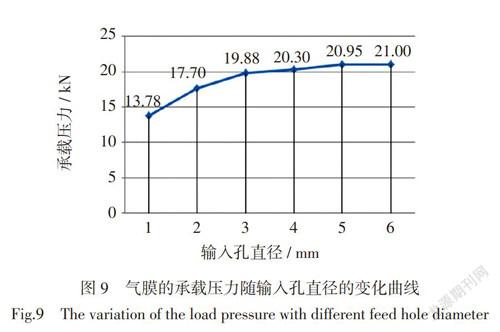
在Fluent软件中求解气膜上支撑平面的压力积分,得到气膜上支撑平面承载压力随输入孔直径的变化曲线(图9)。
如图9所示:在其他外界条件不变时,当输入孔直径小于3 mm时,气膜的承载压力随输入孔直径的增大而线性增大;当输入孔的直径在3~5 mm之间时,气膜的承载压力随输入孔直径的增大线性单位增量变小;当输入孔直径大于5 mm时,气膜的承载压力基本保持不变,由此可见楔形槽中的圆柱孔直径为5 mm左右时,钢带的悬浮支撑可以达到一个稳定的状态。
在保持其他外界条件不变,输入孔直径小于3 mm时,进口输入流量随着输入孔直径的增大而间接符合线性增长规律;当输入孔直径大于3 mm时,进口流量的增幅逐渐下降,即楔形槽中空气的泄漏速度变化幅度降低,空气输入流量逐渐趋于稳定。
3.4 承载压力随楔形角度的变化规律
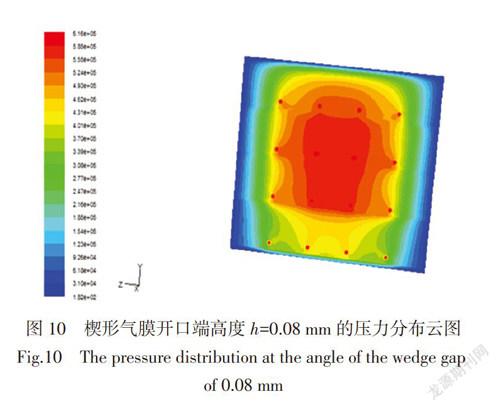
在进行气膜的仿真分析时,通过改变支撑件端面楔形槽中楔形气膜开口端的高度h,达到改变钢带与支撑件接触面之间楔形槽角度的目的,h越高,楔形角度越大。在Gambit软件中建立气膜模型,改变楔形槽气膜开口端的高度h大小,楔形槽中输入孔直径取3 mm,楔形气膜的其他结构不变,对气膜模型进行前处理。设置楔形槽的进口输入压强为0.6 MPa,钢带的运动速度为35 m/s,在Fluent软件中进行流体动力学的仿真计算,得到气膜上支撑平面的压力分布云图以h = 0.08 mm为例(如图10)。
在Fluent软件中对气膜上支撑面的承载压力求积分,得到气膜承载压力随斜槽气膜开口端高度的变化曲线(图11)。
如图11所示:在其他条件不变时,气膜的承载压力随楔形槽气膜开口端的高度(楔形角度)的增加先增大后减小,其变化曲线为开口向下的抛物线,其最大与最小承载压力差值仅有0.41 kN,说明楔形角度对承载压力的影响甚微。
进口输入流量随着斜槽气膜开口端的高度(楔形角度)的增大而线性增长。
当斜槽气膜开口端的高度h>0.09 mm时,随着h的增大,气膜的承载压力逐渐减小,进口输入流量却不断增大,不仅造成了动力的浪费,也使气膜承载能力降低,此时对钢带悬浮支撑的稳定性下降。
4 支撑装置支撑特性的正交试验
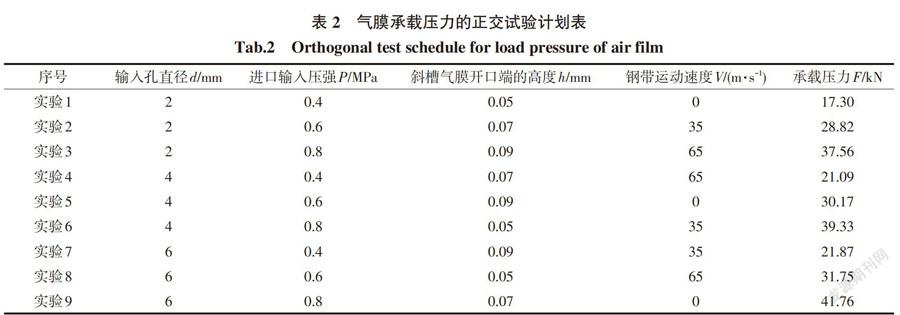
为了使气膜的承载压力分布更加均匀,支撑稳定性增强,在承载压力满足对小型乘用车的支撑需求的前提下,为实现悬浮带式轮胎试验台的低能耗和高效率,现以最小输入压强为目标,根据各个影响因子仿真结果,选用L9(34)正交表,设计了四因素三水平(输入孔直径、输入压强、钢带速度、楔形槽角度)正交试验,由表1因素水平及正交表得出表2中的9种试验方案。通过对试验结果的极差分析,得到最优化的支撑件结构。
4.1 正交试验模拟结果及分析
由表3可知:各因子的影响程度的大小顺序为:输入压强>输入孔直径>斜槽气膜开口端高度>钢带运动速度。其中输入压强对气膜承载压力值的大小影响程度最大。因此,为了获得最大的悬浮支撑力,优化选择的结果为:輸入孔直径选择6 mm,斜槽气膜开口端的高度选择0.07 mm,输入的压强选择0.8 MPa,钢带速度选择65 m/s。比较输入孔直径1 mm,斜槽气膜开口端的高度0.05 mm,承载压力为13.78 kN的悬浮带式轮胎试验台原始设计,优化结构较之能满足20 kN的额定承载压力的需求。在满足额定承载压力的需求下,为了达到减少能耗、降低试验成本的目的,以最小输入压强为目标函数,支撑件上端面的最佳设计结构为:输入压强为0.4 MPa,支撑件上端面输入孔的直径为d=6 mm,楔形斜槽开口端的深度为h=0.07 mm。由此可见,支撑件结构设计时,应该根据不同的设计目标需求,选取合适的参数组合。
5 结论
本文以悬浮带式轮胎试验台气膜悬浮支撑结构为研究对象,研究分析了空气输入压强、输入口直径、钢带运动速度和楔形槽角度对气膜的承载压力的影响,得到如下结论:
1)进口输入压强和楔形槽中的圆柱孔直径是悬浮支撑特性中的主要影响因子,承载压力随进口输入压强和圆柱孔直径的增大而增大,获得使支撑装置具有较优性能的圆柱孔直径。随着进口压强的增大空气的泄露速度加快,因此,进口输入压强和圆柱孔直径减小,能够减少进气流量,达到节能减排的目的,从而提高经济性。
2)斜槽角度和钢带速度对承载压力的影响不大,考虑模拟器静置时楔形槽对钢带的支撑损坏,选取较小的楔形槽开口端高度为宜。均能满足在钢带工作速度范围内对承载压力的需求。
3)由正交试验得到,在满足额定承载压力的需求下,为了达到减少能耗、降低试验成本的目的,以最小输入压强为目标函数,支撑件上端面的最佳设计结构。通过极差分析,得到支撑装置各影响因子对支撑性能影响的主次顺序。结果表明输入压强是支撑压力的最主要影响因素。
参考文献:
[1] 郭孔辉. 汽车操纵动力学原理[M]. 南京:江苏科学技术出版社,2011.
[2] 郭孔辉,杨一洋. 轮胎力学特性试验台的运动学分析[J]机械工程学报,2013,49(20):63-70.
[3] CABRERA J A,ORTIZ A,SIMON A,et al. A versatile flat track tire testing machine[J]. Vehicle System Dynamics,2003,40(4):271-284.
[4] LANGER W J,Flat belt tire tester:US,4344324[P]. 1982-08-17.
[5] LANGER W J,POTTS G R. Development of a flat surface tire testing machine[Z].
[6] CABRERA J A,ORTIZ A,SIMON A,et al. A aversatile flat track tire testing machine[J]. Vehicle System Dynamics,2003,40(4):271-284.
[7] FREUDENMANN T,UNRAU H J,El-HAJI M. Experimental determination of the effect of the surface curvature on rolling resistance measurements4[J]. Tire Science and Technology,2009,37(4):254-278.
[8] BIND K D,MARTIN J F. The calspan tire research facility:design,development and initial test results[C]//SAE Paper 730582,1973.
[9] 楊一洋,许男,郭孔辉,等. 轮胎滑水机理在钢带式高速轮胎试验台上的应用[J]. 吉林大学学报(工学版),2016,46(1):1-7.
[10] 吴波,陈志,李建明,等. 基于 CFD 正交试验的螺旋槽干气密封性能仿真研究[J]. 流体机械,2014,42(1):11-16.
[11] 张直明. 滑动轴承的流体动力润滑理论[M]. 北京:高等教育出版社,1986.
[12] 赵祥. Y7125磨齿机砂轮修整器整体式气浮导轨的研究[D]. 西安:西北工业大学,2013.
[13] 敏政,王乐,魏志国,等. 基于MATLAB技术的滑动轴承油膜压力分布的模拟[J]. 润滑与密封,2008,33(8):51-53,57.
[14] 张鹏高,丁雪兴,魏龙,等. 螺旋槽干气密封润滑气膜特性的数值模拟[J]. 润滑与密封,2010,35(8):74-78.
[15] 靳兆文. 气体润滑技术及其研究进展[J]. 通用机械,2007(3):57-60.
[16] 黄平. 润滑数值计算方法[M]. 北京:高等教育出版社,2012.
[责任编辑 杨 屹]
