低碳经济背景下绿色供应链中政企博弈的研究

唐慧玲

摘要：基于纳什均衡理论和演化博弈理论，研究了绿色供应链中政府和企业关于减排问题的行为博弈。首先根据政府服务大众的职能，创新地以社会福利函数表征了政府目标函数，求解得出政企博弈的纳什均衡策略为：监管、低碳化生产，并对纳什均衡的成立条件做出了合理的经济学解释。然后考虑到实际情况中博弈参与者的不完全理性，修改了政府目标函数。利用双种群演化博弈论描述了政企博弈的过程，剖析出四种不同条件下的演化稳定策略并赋予了经济学含义。最后比较了两种博弈分析的不同点，结合计算得出的博弈均衡策略，分别从政府、企业和消费者的角度提出了政策建议。研究表明：只有政府、企业、民众三方协同努力，政府严格监管且企业自主减排的目标才可能实现。

关键词：政企博弈;低碳经济;绿色供应链;消费者偏好;社会福利;企业减排;纳什均衡;演化博弈

文献标识码：A

文章编号：100228482019（06）010812

在2009年12月于丹麦首都哥本哈根召开的联合国气候变化大会上，各国研究者对全球气候变暖的原因与预防对策展开了讨论。至此之后，“全球变暖”不断在各种场合被提及。2007年全球政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）第四次报告[1]就指出，温室气体的排放（由于温室气体中碳的含量过半，俗称“温室气体排放”为“碳排放”）是直接造成全球气候变暖的重要原因之一。在环境保护的大背景下，我国政府积极出台相应政策以应对环保节能的时代挑战。2007年发布的《中国应对气候变化国家方案》标志着我国政府将气候变化问题上升到国家级别。我国财政部也在积极执行“关于碳排放权交易会计准则制定”项目，具体针对我国会计准则委员会于2016年9月发布的《碳排放权交易试点有关会计处理暂行规定（征求意见稿）》有争议的问题展开研究。我国政府对激发企业节能减排的潜力所做出的这些实际行动，都彰显了我国推动绿色经济发展与转型的决心。

所谓“碳交易机制”就是指政府对供应链企业发放一定配额的碳排放指标，若企业的碳排放额度指标未用完，可以将多余额度指标在碳交易市场中卖出。若企业碳排放量超出额度，则需要到碳交易市场内购买指标[2]。另外，政府为了限制企业碳排放还有一种惩罚机制，就是对超出排放限额的企业罚款而对未超出的企业进行奖励。目前社会大众十分关注企业的社会责任履行情况。企业社会责任（Corporate Social Responsibility，CSR）是指企业除创造经济价值外，对消费者和社区环境所做出的贡献。在低碳经济的时代背景下，供应链中的企业想要追求利益最大化，必须应对好政府的碳排放管理措施以及社会大众的监督，在变化的经济环境中优化自身的减排策略，在长期发展中占据优势。

在倡导环境保护的背景下，绿色供应链中政府监管企业进行减排实际上是政府和企业间的一种行为博弈。当然社会大众最希望看到的结果是政府严格监管并且企业自主减排，这也是对生态环境最有利的结果。在现实情境中，对政企的行为博弈展开分析，有助于从理论层面上对政府和企业的决策行为进行指导，以实现企业自主减排的目标，从而践行环保理念、造福社会。

本文利用博弈理论分析了存在消费者偏好的低碳供应链中，政府与企业各自的最优博弈策略选择问题。首先，考虑到政府服务于社会大众的职能，不同于以往文献中以政府利润最大化为目标函数进行博弈分析，本研究将政府目标设定为大众福利最大化，对政府和企业的非合作博弈均衡进行求解;然后考虑到实际情况中博弈参与者为不完全理性，修改政府的目标函数，利用演化博弈理论对政企博弈进行再次研究;最后针对企业自主减排的目标，分别从政府、企业、消费者的角度提出了政策建议。

本文的贡献在于：第一，分别利用纳什均衡理论和演化博弈理论对同一问题进行研究，两种博弈分析各具优势且都合理描述出了政企博弈的特点，对博弈的预测结果可以进行相互比较，有助于问题的分析。第二，在博弈模型构造时充分考虑各种影响因素，包括消费者的偏好等。由于两种博弈分析的前提假设条件不同，设定了符合各自情景的政府目标函数，遵循了研究的嚴谨性。第三，结合本文两种博弈的研究结果，针对企业自主减排的目标，从政府、企业和消费者三个角度分别提出了具有可操作性的政策建议。

一、相关文献综述

目前，以绿色供应链为研究背景的文献已较为丰富，研究的热点问题为优化绿色供应链上企业（制造商）的行为决策。Benjaafar等[3]运用简单线性规划模型，分析了碳排放管理对供应链上政府、企业决策的影响，对其今后的策略制定提供了有意义的建议。Hsu等[4]研究了低碳供应链中供应商选择的问题，利用决策与试验评价实验室法（DEMATEL）确定了供应商的选择标准。Hoejmose等[5]研究了制造商在有碳管理限制的经济环境中如何衡量碳排放量与利润的关系，文章旨在建立模型找到减排和增加利润的平衡点。李兵等[6]研究了存在碳收费的供应链中各节点上的库存管理问题，并给出了最优库存的具体实现方案。在存在碳交易的供应链上，王芹鹏等[7]从消费者偏好的视角研究了单个供应商、单个零售商组成的两阶段供应链中，最优订货量和最优减排水平的问题。陈东彦等[8]考虑了存在减排投资效果滞后效应影响的低碳供应链中，分散式决策和集中式决策下的最优减排投入与零售定价的策略。

有的研究关注低碳供应链管理的优化，以提高供应链的盈利水平。Ramudhin等[9]在引入了碳交易市场的绿色供应链设计中，优化了碳交易市场中提供选择的混合模型，使供应商和制造商能够充分利用碳交易市场提供的选择以增加供应链利润。Boonsothonsatit等[10]利用模糊目标规划的方法，设计了一个通用的决策支持系统（DSS），可以帮助决策者在低碳供应链设计中抉择出拥有适当运输策略的最优供应商。传统的绿色供应链研究文献，其背景多数设定为供应商、制造商和零售商组成的三阶段供应链，或其中相邻两个节点组成的两阶段供应链。而近年来随着社会可持续发展的深入，资源的循环利用受到重视，废品回收以及再制造是企业必须要关注的问题。高鹏等[11]提出了闭环再制造供应链，此种供应链更符合存在废品回收利用的经济环境。

低碳供应链中上下游企业的最优策略是相互制约的，这种策略选择过程实际是一种博弈行为。王永平等[12]运用演化博弈模型分析了供应链中上下游企业合作、竞争态势的演化趋势，其结论为演化趋势的关键在于支付矩阵和初始条件。马秋卓等[13]将碳交易中心引入了上下游企业间的碳交易市场，建立一个网链式的供应链结构，考虑了多个博弈参与人及他们之间的均衡决策。Hu等[14]以演化博弈的分析方法研究了核心企业和供应商之间的合作策略，结果表明企业选择道路的独立性以及合作的成本和收益直接影响两者在低碳供应链中的行为博弈。付秋芳等[15]研究了供应商与制造商碳减排投入的演化博弈模型，最后分析得到了供应商和制造商的演化博弈策略。何伟军等[16]采用非对称动态演化博弈模型，在绿色供应链的背景下研究了企业协作发展中的策略选择问题，发现在惩罚契约机制不存在的情况下，演化博弈的均衡结果并不总是双方都会选择积极协作发展，并在此基础上展开了其他分析。在社会越来越关注企业碳足迹的态势之下，消费者对于低碳商品的偏好也愈发明显。早在2010年中国新闻网就有报道称“都市低碳意识增强，节能家居产品销售走俏”[17]，表明现在群众的环保行动逐渐走入细节，“低碳、节能、绿色”等无疑是今后制造类企业所追求的目标。王芹鹏等[18]研究了企业减排策略的選择，首次将低碳、供应链管理以及演化博弈结合起来，分析了四种不同投资组合中上下游企业间的博弈均衡，得出了几个演化均衡策略。骆瑞玲等[19]考虑了存在不确定需求的碳交易市场的供应链，加入消费者行为影响因素，研究了碳排放交易政策和投资减排对供应链中企业相关决策的影响。

政府在低碳供应链中作为规则缔约者和监管者，其行为决策直接影响着供应链内企业的最优策略选择。李媛等[20]研究得出比较有效的政府管理机制为分阶段提高碳税，但其分析时未考虑消费者偏好的影响。杨仕辉等[21]研究表明政府实施碳补贴政策能够激励供应链成员减排，此时供应链成员的一体化程度越高，碳补贴政策的效果就越好。崔连标等[22]运用环境版全球贸易的分析模型，探讨了三种政策情景下政府征收碳关税是否为一个有效的减排政策。其研究结果表明征收碳关税并不能有效地使企业自主减排，而企业在基于成本公平性原则下所做出的减排是大于被征收碳关税时的减排的。孙夙鹏等[23]构建了企业、政府和环境非政府组织（NGO）的三方演化博弈模型及其动态复制方程，对模型结果的10个均衡点进行了稳定性分析，并对这三方的交互行为演化过程进行了数值仿真。李友东等[24]利用演化博弈论分析了政府和核心企业之间的减排策略博弈，讨论了演化稳定策略，但其未考虑消费者偏好的影响。张国兴等[25]利用信号博弈刻画了低碳供应链中政企间的策略选择行为，研究提出应建立全面多维度的考核指标，充分发挥公众、媒体的监督作用，有效制约企业间的合谋行为并使得政府减排补贴政策成功发挥作用。

关于绿色供应链中政府和企业间博弈的相关研究存在一定问题：第一，在博弈过程刻画时未考虑到市场内消费者行为因素;第二，对政府的角色和利益追求考虑不完善，可能存在政府过分施压而导致企业减排积极性被削弱的情况。鉴于此，本文拟运用纳什均衡理论和演化博弈理论去刻画低碳供应链中政府与企业博弈的过程，并充分考虑消费者偏好因素的影响和政府服务大众的职能，求解出两种博弈的均衡策略。

二、低碳供应链中政府与企业博弈的纳什均衡分析

（一）模型构建与研究假设

运用博弈论研究供应链中的相关问题已被众多学者实践[26]，本文研究存在消费者偏好的低碳供应链中政府监管企业减排的活动，拟采用纳什均衡理论[27]对此博弈过程进行分析。根据政府监管企业减排时具有独立性和客观性的特点，此时政企的博弈属于非合作博弈，即博弈双方都为了自身利益的最大化进行自主选

择，与策略环境中他人的选择无关，此时政府与企业的非合作博弈均衡就是一个纳什均衡（Nash equilibrium）。政府和企业在博弈过程中都分别有两种策略可以选择，具体策略组合矩阵见表1。

本文为政府设计了一种激励企业减排的制度，具体为根据企业排放程度的不同而征收不同税率的碳税，同时对低碳生产的企业进行补贴。假设政府监管时的成本为固定的cg，若政府监管时发现企业低碳化生产就对其征收相对较低的碳排放税，单位碳排放税率为τ;若发现企业高碳化生产就对其征收相对较高的碳排放税，单位碳排放税率为τ′，显然τ′>τ。政府希望企业能自觉减排，若发现企业采取低碳化生产策略，则政府会对此类企业按其减排水平Δe进行补贴，补贴率为α，实际补贴额为αΔe。

在企业的生产经营活动中，其边际生产成本为ce，产品的销售量为q。本文研究单生产周期，企业生产单位产品时的碳排放量为e0，而Δe为企业的减排总量。根据田盈等[2829]关于供应链企业成本函数的设定及其性质的描述，本文将企业的减排成本函数设为C（Δe）=ξ（Δe）2/2，ξ为单位减排量投资系数且ξ>0。减排成本函数需满足条件：C（Δe）≥0，C′（Δe）>0，C″（Δe）>0。其经济学含义为：企业减排水平越高，所需要的技术支持越强，因此减排投资成本越多（C′（Δe）>0）;随着减排水平的不断提高，其减排的边际效用是递减的，符合实际情况。换言之，边际减排投资成本是递增的（C″（Δe）>0）。产品销售价格为p=v-φq+γΔe，其中v为顾客的保留价格，且v为一常数。φ是随着销售量q的增多，顾客的支付意愿减少的系数。也可将p=v-φq解释为需求函数，p与q成反比关系。γ为消费者对低碳商品的偏好程度系数，本文考虑绿色消费者，对于他们来说γ>0。企业进行低碳化生产时生产成本减少，如生产环节中材料的回收利用、化石燃料消耗量的减少等都能使生产成本降低，也可以理解为收益的增加，设为βq。其中，β为单位产量收益增加系数。将上文中所设定的参数和变量进行归纳，具体见表2。

在求解此博弈的纳什均衡解时，将政府和企业都设定为单个具有代表性的个体。假设政府与企业间的信息都是完全的，即企业可以观察到政府是否进行监管活动。再假设政府与企业都为完全理性的，选择博弈策略时都是为了个人利益最大化。又考虑到政府为社会大众服务的职能及政府的完全理性，这里将政府的收益函数设定为社会福利函数W，与以往同类研究中设定为税收收入减去监管成本[24]相区别，将政府收益视为社会民众的利益更符合现实情景。在不改变问题本质的基础上，对文中政企博弈的模型做出如下假设：

（1）博弈双方拥有完全信息且为完全理性的。

（2）企业的“碳足迹”记录是公开的，其生产的商品是否为低碳商品也有明确标注，绿色消费者可以便捷地判断出自己的偏好程度。

（3）政府博弈的目标为大众福利最大化。

（4）碳减排技术的研发与生产技术的研发是相互独立的，本文假设企业的生产技术水平是一定的，因此其边际生产成本ce是固定的。

（5）假设博弈中的企业生产时的单位碳排放量e0一定大于政府制定的低碳商品单位碳排放量标准，也就是说文中参与博弈的企业若不进行减排就一定是高碳化生产的。另外假设企业如果决定采取低碳化生产策略，那么其碳排放量至少会降至政府给出的低碳生产碳排放量标准，否则其减排是无意义的。

（二）政企双矩阵博弈的纳什均衡

社会福利函数实际是社会中个人福利的总和，本研究将社会中所有个人视为一个大众群体，此社会中所有个人福利之和可用大众群体的福利进行替代，而福利水平可用效用函数进行表示。根据Bergson[30]于1938年提出的社会福利函数概念，社会福利值被影响其变化的实值变量构造的函数所决定，而具体函数形式没有任何规定。借用这一概念，在本文绿色供应链的研究背景下，对于大众群体而言，影响其效用函数W的主要变量为产品价格p、企业排放总量e0q-Δe、企业低碳化生产时政府税收收入τ（e0q-Δe）-αΔe-cg或企业高碳化生产时政府税收收入τ′e0q-cg。对以上几个变量与大众群体效用的关系做出如下解释：消费者对产品价格是敏感的，按常理来说理性消费者是期望低价的（文中消费者是偏好绿色企业的，并且为理性消费者），即价格与大众福利成反比;绿色消费者认为碳排放总量越低越好，即碳排放总量与大众福利成反比;政府税收收入可作为公共基础设施建设资金，属于对大众的转移支付，因此政府税收收入与大众福利成正比。

设权重ωi>0（i=1，2，3），且∑3i=1ωi=1。社会福利函数可表示为

W=-ω1p-ω2E+ω3T（1）

其中，p为产品价格，E为企业排放总量，T为政府税收收入。

在式（1）中，令ω1=ω2=ω3=13，则政府在表1中的策略组合下的目标函数分别为

W11=-13p-13（e0q-Δe）+13[τ（e0q-Δe）-αΔe-cg]

W12=-13p-13e0q+13（τ′e0q-cg）

W21=-13p-13（e0q-Δe）

W22=-13p-13e0q

设G=〈N，S1，S2，u1，u2〉为政府和企业的有限博弈，且S1={α1，α2}，S2={β1，β2}，这时两者的收益矩阵分别为

A=

-13p-13（e0q-Δe）+13[τ（e0q-Δe）-αΔe-cg]-13p-13e0q+13（τ′e0q-cg）

-13p-13（e0q-Δe）-13p-13e0q

B=

（v-φq+γΔe-ce+β）q-ξ（Δe）22-τ（e0q-Δe）+αΔe（v-φq-ce）q-τ′e0q

（v-φq+γΔe-ce+β）q-ξ（Δe）22（v-φq-ce）q

對G的收益函数做局部变换，分别对A进行列变换，对B进行行变换后可得

A′=τ（e0q-Δe）-αΔe-cg00-（τ′e0q-cg）

B′=

（γΔe+β）q-ξ（Δe）22+（τ+α）Δe+（τ′-τ）e0q0

0ξ（Δe）22-（γΔe+β）q

令

a1=τ（e0q-Δe）-αΔe-cg

a2=-（τ′e0q-cg）

b1=（γΔe+β）q-ξ（Δe）22+（τ+α）Δe+（τ′-τ）e0q

b2=ξ（Δe）22-（γΔe+β）q

记政府的混合策略为X=（x，1-x），企业的混合策略为Y=（y，1-y）。政府和企业的期望收益分别为

E1（x，y）=（x1-x）a100a2y1-y=a1xy+a2（1-x）（1-y）（2）

E2（x，y）=（x1-x）b100b2y1-y=b1xy+b2（1-x）（1-y）（3）

分别对式（2）（3）即政府和企业的期望收益求一阶导数：

E1x=（a1+a2）y-a2

E2y=（b1+b2）x-b2

政府的最优反应是对固定的Y，选择X，使其期望收益E1最大。同理，企业的最优反应是对固定的X，选择Y，使其期望收益E2最大。政企博弈的纳什均衡策略可以通过比较参数a1、a2、b1、b2的大小来得到。由参数含义分析可得：a1>0，a2<0，b1>0，b2<0。通过对模型的分析，可得到以下纳什均衡解释：

（1）a1>0，a2<0。a1+a2=（τ-τ′）e0q-（τ+α）Δe，因为τ<τ′、τ+α>0，所以a1+a2<0，a2a1+a2>1。因而y<a2a1+a2，E1x>0。所以政府的最优反应为x（y）=1，y∈[0，1]。

（2）b1>0，b2<0。b1+b2=（τ+α）Δe+（τ′-τ）e0q，因为τ<τ′、τ+α>0，所以b1+b2>0，显然E2y>0。所以企业的最优反应为y（x）=1，x∈[0，1]。

故此时的纳什均衡策略为一纯策略（监管、低碳化生产）[31]。

（三）政企纳什均衡策略的经济学解释

分析以上纳什均衡策略的成立条件，可得到如下研究结论：

（1）当a1>0时，有τ（e0q-Δe）-αΔe-cg>0τ（e0q-Δe）>αΔe+cg，即政府对企业生产活动中的排放情况进行严格监管且企业低碳化生产时，政府的税收收入大于政府监管的固定成本与政府对低碳生产企业的补贴之和，也就是此时政府的净税收收益大于零。因此政府开展监管活动不需要财政收入的补贴，也间接地不会加重民众的税收负担，对于民众来说是有利的。

（2）当a2<0时，有τ′e0q-cg>0，即政府监管且企业高碳化生产时，政府净税收收益大于零。当企业采取高碳排放方式进行生产时政府应当加大对高碳化生产企业的惩罚力度，进而有效地控制企业高碳化生产的情况，迫使其放弃这种生产策略从而降低碳排放使环境得到保护。

（3）由于b1和b2的大小彼此相关，若b2<0，则ξ（Δe）2/2-（γΔe+β）q<0。显然有（τ+α）Δe+（τ′-τ）e0q>0，那么（γΔe+β）q-ξ（Δe）2/2+（τ+α）Δe+（τ′-τ）e0q>0，即b1>0。若b2>0，b1的大小判断较为复杂，符号不能确定，所以略去此种情况，则b1>0，b2<0，其中b2<0可解释为企业选择低碳化生产策略时，其额外收入大于减排成本，加之政府监管时会对低碳化生产的企业进行补贴，以上因素都会促使企业理性地选择低碳化生产策略。

综上所述，在政府和企业的策略博弈中，其纳什均衡策略为一纯策略（监管、低碳化生产）。这个结果有利于民众，该纳什均衡策略为合理的。

三、低碳供应链中政府与企业的演化博弈分析

（一）模型构建与研究假设

在实际情况中，政府和企业进行博弈时具有完全信息和完全理性的条件是较难达到的。博弈双方常常存在信息不对称，即对他人的收益或目标等情况掌握不完全，并且很难保证所做出的决策是最佳的，此时可运用演化博弈论进行分析。演化博弈论最早起源于生物学的研究，在Fisher与Hamilton等遗传生态学家研究动、植物的合作与冲突的行为博弈时萌芽。1973年Smith等[32]首次提出演化稳定策略（Evolutionary Stable Strategy，ESS），标志着演化博弈论的诞生。演化博弈的分析优势在于不要求博弈参与者完全理性且拥有完全信息，正好贴合本文研究背景的实际情况。运用演化博弈理论对政企博弈进行分析时，将博弈双方分别假设为群体，演化稳定策略就是政府群体与企业群体根据环境不断调节最优策略的结果。在不改变问题本质的基础上，对政企的演化博弈模型做出如下假设：

（1）博弈双方拥有不完全信息且为有限理性的。

（2）企业的“碳足迹”记录是公开的，其生产的商品是否为低碳商品也有明确标注，绿色消费者可以顺利判断出自己的偏好程度。

（3）政府博弈的目标为利润最大化。

（4）碳减排技术的研发与生产技术的研發是相互独立的，本文假设企业的生产技术水平是一定的，因此其边际生产成本ce是固定的。

（5）假设博弈中的企业生产时的单位碳排放量e0一定大于政府制定的低碳商品单位碳排放量标准，也就是说文中参与博弈的企业若不进行减排就一定是高碳化生产的。另外假设企业如果决定采取低碳化生产策略，那么其碳排放量至少会降至政府给出的低碳生产碳排放量标准，否则其减排是无意义的。

（二）政企博弈的演化稳定策略

1.政企演化过程中的收益分析

在上文的讨论基础上，继续使用政企纳什均衡模型中设定的各个参数和变量。由于现假设博弈双方均为不完全理性，政府具有“短视”的特点，因此较为看中个人短期收益而忽略社会大众的诉求。此时政府的收益函数不再设定为社会福利函数，修改为政府的监管收益。政企演化博弈的策略组合矩阵同表1，博弈的收益矩阵见表3。

假设在此博弈过程中，政府和企业都随机独立地选择自己的策略，且此策略博弈过程不断重复。政府群体采取监管措施的比例为a，不采取监管措施的比例为1-a。企业群体低碳化生产的比例为b，高碳化生产的比例为1-b。政府监管时的期望收益为UGY，不监管时的期望收益为UGN，种群平均收益为G。企业低碳化生产时的期望收益为UEY，高碳化生产时的期望收益为UEN，种群平均收益为E。

政府群体采取不同策略时的适应度为

UGY=b[-cg+τ（e0q-Δe）-αΔe]+（1-b）（-cg+τ′e0q）=[（τ-τ′）e0q-（τ+α）Δe]b-cg+τ′e0q（4）

UGN=0（5）

G=aUGY+（1-a）UGN=[（τ-τ′）e0q-（τ+α）Δe]ab-cga+τ′e0qa（6）

企业群体采取不同策略时的适应度为

UEY=a[（v-φq+γΔe-ce+β）q-ξ（Δe）22-τ（e0q-Δe）+αΔe]+（1-a）[（v-φq+γΔe-ce+β）q-ξ（Δe）22]=（αΔe-τe0q+τΔe）a+（v-φq+γΔe-ce+β）q-ξ（Δe）22（7）

UEN=a（v-φq-ce）q-τ′e0qa+（1-a）（v-φq-ce）q=（v-φq-ce）q-τ′e0qa（8）

E=bUEY+（1-b）UEN=（αΔe-τe0q+τΔe）ab+（γΔe+β）qb+τ′e0qa（b-1）+（v-φq-ce）q-ξ（Δe）22b（9）

2.复制动态方程与演化均衡

（1）政府群体采取监管策略时的复制动态方程。

根据Malthusian方程[33]，政府群体选择监管策略时，此方案的数量增长率dx/dtx等于其适应度UGY减去平均适应度G，其中t为时间。由式（4）—（6）可得政府群体选择监管策略比例的复制动态方程为

F（a）=dadt=a（UGY-G）=a（1-a）{[（τ-τ′）e0q-（τ+α）Δe]b-cg+τ′e0q}

若b=cg-τ′e0q（τ-τ′）e0q-（τ+α）Δe，则F（a）=0，此时所有水平均为稳态。

若b≠cg-τ′e0q（τ-τ′）e0q-（τ+α）Δe，由F（a）=0可得a=0和a=1为a的两个稳定点。

对F（a）求a的一阶导数：

dF（a）da=（1-2a）{[（τ-τ′）e0q-（τ+α）Δe]b-cg+τ′e0q}

政府的演化稳定策略要求dF（a）da<0，下面对不同情况进行分析：

①若τ′e0q-cg<0，则

τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q<0，恒有

b>τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q，此时

dF（a）daa=0<0，

dF（a）daa=1>0，则a=0为平稳点。

②若τ′e0q-cg>（τ+α）Δe+（τ′-τ）e0q，即

τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q>1，恒有

b<τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q，此时

dF（a）daa=0>0，

dF（a）daa=1<0，则a=1为平稳点。

③若0<τ′e0q-cg<（τ+α）Δe+（τ′-τ）e0q，即

0<τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q<1，此时分情况讨论：当

b>τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q时，因为

dF（a）daa=0<0，

dF（a）daa=1>0，则a=0为平稳点;当

b<τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q时，因为

dF（a）daa=0>0，

dF（a）daa=1<0，则a=1为平稳点。

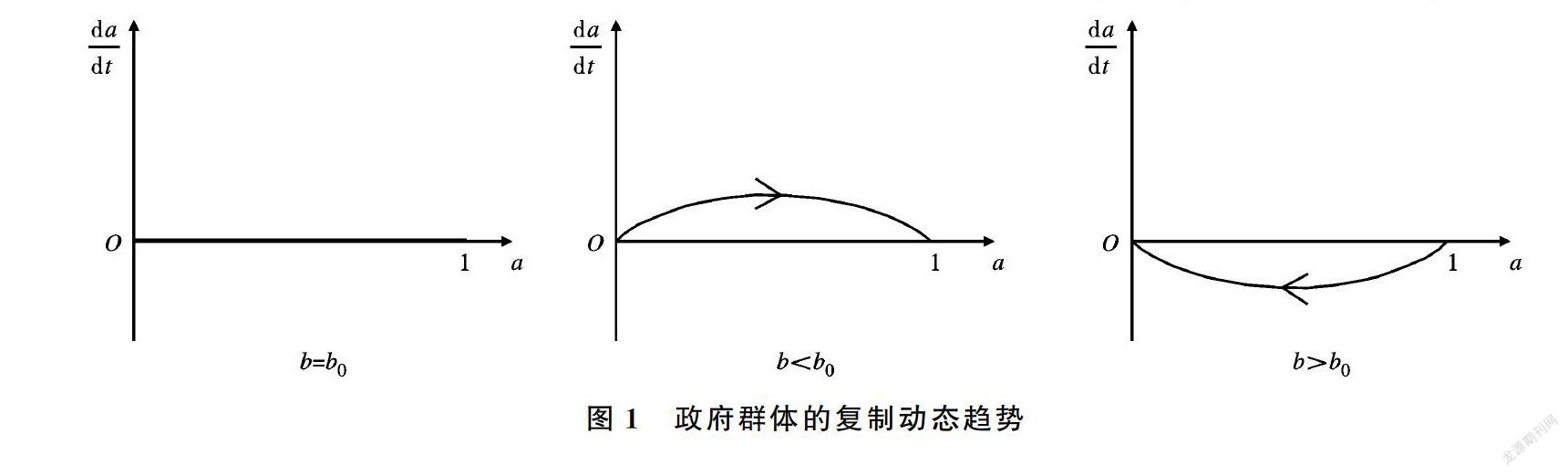
政府群体采取监管策略的复制动态趋势如图1所示，其中bo=τ′e0q-cg（τ+α）Δe+（τ′-τ）e0q。

（2）企业群体采取低碳化生产策略时的复制动态方程。

同计算政府群体选择监管策略比例的复制动态方程类似，企业群体选择低碳化生产策略比例的动态复制方程可由式（7）—（9）得出：

F（b）=dbdt=b（UEY-E）=

b（1-b）[（τ′-τ）e0q+（α+τ）Δe]a-ξ（Δe）22+（γΔe+β）q

若a=ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe，则F（b）=0，此时所有水平均为稳态。

若a≠ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe，由F（b）=0可得b=0和b=1为b的两个稳定点。

对F（b）求b的一阶导数：

dF（b）db=（1-2b）[（τ′-τ）e0q+（α+τ）Δe]a-ξ（Δe）22+（γΔe+β）q

企业的演化稳定策略要求dF（b）db<0，下面对不同情况进行分析：

①若ξ（Δe）22-（γΔe+β）q<0，则

ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe<0，恒有

a>ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe，此时

dF（b）dbb=0>0，

dF（b）dbb=1<0，则b=1为平稳点。

②若ξ（Δe）22-（γΔe+β）q>（τ′-τ）e0q+（α+τ）Δe，即

ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe>1，恒有

a<ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe，此时

dF（b）dbb=0<0，

dF（b）dbb=1>0，则b=0为平稳点。

③若0<ξ（Δe）22-（γΔe+β）q<（τ′-τ）e0q+（α+τ）Δe，

0<ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe<1，此时分情况讨论：当

a<ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe时，因为

dF（b）dbb=0<0，

dF（b）dbb=1>0，则b=0为平稳点;当

a>ξ（Δe）22-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe时，因为

dF（b）dbb=0>0，

dF（b）dbb=1<0，则b=1为平稳点。

企业群体采取低碳化生产的复制动態趋势如图2所示，其中a0=ξ（Δe）2/2-（γΔe+β）q（τ′-τ）e0q+（α+τ）Δe。

（3）政企演化博弈的均衡。

在演化博弈的过程中，没有外力作用时，政企博弈系统会到达均衡状态（rest state），均衡状态能刻画出系统的真实状态。均衡状态通常由平稳点来描

述，通过上述讨论可知政企演化博弈系统的平稳点有5个：（0，0）、（0，1）、（1，0）、（1，1）、（a0，b0）。因此政企演化系统的轨迹图可被画出，它描述了政府和企业的动态系统的演化过程。分析政企的演化博弈动态过程，结合图3可得到不同的均衡状态的研究结论，见表4。

（三）演化博弈均衡的经济学解释

通过建立政企间演化博弈的模型，分析不同策略在博弈活动中的稳定性及博弈演化的趋势。根据上文的分析，比较政企演化博弈的各种均衡结果，可以得出4种稳定策略，分别赋予其具体的经济含义后解释如下：

（1）当τ′e0q-cg<0时，即τ′e0q<cg时，a=0是演化稳定策略。若政府监管时向高碳化生产企业征收的税款小于政府监管的固定成本，那么政府群体最终都会选择不监管的策略。

（2）当τ′e0q-cg>（τ+α）Δe+（τ′-τ）e0q时，即τ（e0q-Δe）-αΔe>cg时，a=1是演化稳定策略。若政府监管时向低碳化生产企业征收的税款与政府发放给该类企业的补贴之差大于政府监管的固定成本，即政府监管且企业低碳化生产时政府的净收益大于零（τ（e0q-Δe）-αΔe-cg>0），那么政府群体最终都会选择监管的策略。

（3）当ξ（Δe）2/2-（γΔe+β）q<0时，即ξ（Δe）2/2<（γΔe+β）q时，b=1是演化稳定策略。若企业低碳化生产时为减排技术投资的成本小于其由于生产技术的改进而增加的收益以及由于消费者偏好而增加的收益之和，那么企业群体最终都会选择低碳化生产的策略。

（4）当ξ（Δe）2/2-（γΔe+β）q>（τ′-τ）e0q+（α+τ）Δe时，即ξ（Δe）2/2+τ（e0q-Δe）-（γΔe+β）q-αΔe>τ′e0q时，b=0是演化稳定策略。综合考虑企业的两种生产策略，若企业低碳化生产的总成本（ξ（Δe）2/2+τ（e0q-Δe），即减排投资和缴纳税款之和）大于其总收入（（γΔe+β）q+αΔe，即改进生产技术的额外收入、由于消费者偏好而增加的收益、政府补贴这三者之和），且低碳化生产的总成本与总收入之差大于企业高碳化生产时的赋税，那么企业群体最终都会选择高碳化的生产策略。

四、两种博弈分析的比较

本文对存在消费者偏好的低碳供应链中政府监管企业进行减排这一活动采用了两种博弈理论进行分析。运用两种博弈理论分析时存在一些不同点：

第一，博弈对象不同。在求解纳什均衡时将政府与企业假设为单个具有代表性的个体，实际上纳什均衡分析也适合多人博弈的情况，此处为了方便分析，只研究了单个政府和单个企业的情况。演化博弈分析时为了符合博弈的前提假设条件，将博弈双方设定为政府群体和企业群体，从研究背景来看，群体的设定也更加符合实际情况。而纳什均衡分析更为简单，且得出的均衡策略更加稳定占优。

第二，前提假设条件不同。纳什均衡分析时假设博弈双方都是完全理性且拥有完全信息，考虑到政府服务大众的职能，分析时将政府收益函数设定为社会福利函数。而演化博弈分析时假设博弈双方都为不完全理性且拥有不完全信息，根据政府“短视”的特征，即政府更为看中短期内的个人利益而未考虑到社会大众的长远利益，此处将政府收益函数修改为其监管收益。因此，在两种博弈分析中政府的收益函数发生了合理的转变。

第三，博弈分析结果不同。由于两种博弈的前提假设和分析条件都不相同，其博弈的结果也有较大区别。纳什均衡策略为一个纯策略，而演化稳定策略有四种，分别根据不同演化动态分析得出。演化博弈的稳定策略虽为静态概念，但它能够描述出系统的动态性质[34]。在本文的研究背景下，纳什均衡可以描述出政企博弈的一般均衡结果。而演化博弈分析得出的4个演化稳定策略分别描述了政企博弈的动态特征，其演化均衡结果取决于一些博弈参数的初始设定，博弈结果较为复杂。两种均衡各有优点，都可以很好地描述出政企博弈的特点。

五、结论与启示

本文利用纳什均衡理论和演化博弈理论，研究了绿色供应链中政府和企业关于减排问题的行为博弈，得到以下主要结论：

其一，政企博弈的纳什均衡策略为一纯策略（监管、低碳化生产），即无论对方的选择如何，政府都会采取对企业进行碳排放监管的政策，而企业会采取低碳化生产的策略。

其二，政企博弈的演化稳定策略：

（1）当政府监管时向高碳化生产企业征收的税款小于政府监管的固定成本，政府群体会选择不监管的策略;

（2）当政府监管时向低碳化生产企业征收的税款与政府发放给该类企业的补贴之差大于政府监管的固定成本（政府监管且企业低碳化生产时政府的净收益大于零），政府群体会选择监管的策略;

（3）当企业低碳化生产时为减排技术投资的成本小于其由于生产技术的改进而增加的收益以及由于消费者偏好而增加的收益之和，企业群体会选擇低碳化生产的策略;

（4）综合考虑企业的两种生产策略，若企业低碳化生产的总成本大于其总收入，且低碳化生产的总成本与总收入之差大于企业高碳化生产时的赋税，那么企业群体最终会选择高碳化的生产策略。

基于以上研究结论，可对政府群体制定碳税制度和补贴制度以及企业的生产经营决策提出以下建议：

第一，政府进行监管时应区别对待减排和不减排的企业，特别地，应对低碳化生产企业进行补贴。具体操作办法为设置不同的碳排放征税税率，以及低碳生产的补贴率：τ（对低碳化生产企业的征税率）、τ′（对高碳化生产企业的征税率）、α（对低碳化生产企业的补贴率）。设置税率和补贴率时应注意其合理性，τ′应满足τ′e0q>cg（政府向高碳化生产企业所征税款大于监管固定成本）;τ和α应满足τ（e0q-Δe）-αΔe>cg（政府向低碳化生产企业所征税款与发放的补贴之差大于监管固定成本）;τ、τ′、α三者应满足ξ（Δe）2/2+τ（e0q-Δe）-（γΔe+β）q-αΔe>τ′e0q（企业分别采取不同生产策略时，总成本与总收入的差值大于高碳化生产时的赋税）。政府在制定碳税制度和补贴制度时若满足了上述条件，政府和企业的演化博弈便会趋向于稳定状态（监管、低碳化生产）。同时因为监管时征收的税款减去固定监管成本后总有富余，则不会加重大众的税收负担，如此制定的碳税政策是为大众所能接受的。

第二，企业面对政府出台的碳税政策，可以通过合理减排来追求利润最大化。在低碳化生产时应注意减排程度Δe的合理性，即Δe应满足ξ（Δe）2/2+τ（e0q-Δe）-（γΔe+β）q-αΔe>τ′e0q（企业低碳化生产时的总成本与总收入之差大于高碳化生产时的赋税），这样才能让企业在与政府的演化博弈中使低碳化生产这一策略达到稳定。

第三，在政府监管企业减排的策略博弈中，消费者的作用也不容忽视。消费者的选择决定着企业是否会长期减排，因为消费者偏好系数γ影响着企业最终制定的产品价格，具体γ应满足（γΔe+β）q>ξ（Δe）2/2（企业低碳化生产时减排增加收益与消费者偏好增加收益之和大于其减排投资成本）。满足上述条件时，政企演化博弈的稳定状态才为监管、低碳化生產。

第四，为了实现企业自主减排的目标可从三个方面进行努力：政府制定合理的碳税政策、企业合理地进行减排、消费者积极支持低碳商品。在低碳经济时代，人人参与减排是最终的目的，现代理性消费者应该了解并支持低碳商品。政府也可以利用媒体进行低碳商品的宣传，力求让民众认识低碳商品，了解其好处及环保意义等。同时消费者还可以发挥中立监督者的作用，政府也应制定相关政策以保证消费者可以通过有效途径对监管不力、乱排乱放等现象进行监督和举报。只有政府、企业、民众三方共同协作努力，政府严格监管、企业自主减排的最终目标才可能实现。

参考文献：

[1]IPCC. Climate change 2007： Synthesis report[R]. Geneva Switzerland， 2007.

[2]杨磊， 张琴， 张智勇. 碳交易机制下供应链渠道选择与减排策略[J]. 管理科学学报， 2017（11）： 7587.

[3]Benjaafar S， Li Y， Daskin M. Carbon footprint and the management of supply chains： Insights from simple models[J]. IEEE Transactions on Automation Science and Engineering， 2013， 10（1）： 99116.

[4]Hsu C W， Kuo T C， Chen S H， et al. Using DEMATEL to develop a carbon management model of supplier selection in green supply chain management[J]. Journal of Cleaner Production， 2013， 56（10）： 164172.

[5]Hoejmose S U， Roehrich J， Grosvold J. Is doing more doing better？ The relationship between responsible supply chain management and corporate reputation[J]. Industrial Marketing Management， 2014， 43（1）： 7790.

[6]李兵， 付新玥， 刘金， 等. 面向低碳的供应链节点最优库存控制策略[J]. 统计与决策， 2012（12）： 4446.

[7]王芹鹏， 赵道致. 消费者低碳偏好下的供应链收益共享契约研究[J]. 中国管理科学， 2014（9）： 106113.

[8]陈东彦， 黄春丽. 滞后效应影响下低碳供应链减排投入与零售定价[J]. 控制与决策， 2018（9）： 16861692.

[9]Ramudhin A， Chaabane A， Kharoune M， et al. Carbon market sensitive green supply chain network design[C]. IEEE International Conference on Industrial Engineering & Engineering Management， 2009.

[10]Boonsothonsatit K， Kara S， Kayis B， et al. Weighted additive fuzzy goal programming based decision support system for green supply network design[C]. IEEE International Conference on Industrial Engineering & Engineering Management， 2014.

[11]高鹏， 聂佳佳， 谢忠秋. 存在绿色消费者的再制造供应链信息分享策略[J]. 管理工程学报， 2014（4）： 193200.

[12]王永平， 孟卫东. 供应链企业合作竞争机制的演化博弈分析[J]. 管理工程学报， 2004（2）： 9698.

[13]马秋卓， 宋海清， 陈功玉. 考虑碳交易的供应链环境下产品定价与产量决策研究[J]. 中国管理科学， 2014（8）： 3745.

[14]Hu Y， Li Y. Study on evolutionary game between core enterprise and suppliers in green supply chain[C]. International Conference on Computer & Management， 2011.

[15]付秋芳， 忻莉燕， 马士华. 惩罚机制下供应链企业碳减排投入的演化博弈[J]. 管理科学学报， 2016（4）： 5670.

[16]何伟军， 吴君， 蔡艳伟. 绿色供应链企业协作发展动态演化博弈分析[J]. 供应链管理， 2015（18）： 171174.

[17]李映民， 张乾铄， 黄雪琴. 都市低碳意识渐强， 节能家居产品销售走俏 [EB/OL]. （20100405）[20150420]. http： ∥www.chinanews.com/cj/cj hbht/news/2010/04 05/2207763.shtml.

[18]王芹鹏， 赵道致， 何龙飞. 供应链企业碳减排投资策略选择与行为演化研究[J]. 管理工程学报， 2014（3）： 181188.

[19]骆瑞玲， 范体军， 夏海洋. 碳排放交易政策下供应链碳减排技术投资的博弈分析[J]. 中国管理科学， 2014（11）： 4453.

[20]李媛， 赵道致. 低碳供应链中政府监管企业减排的演化博弈模型[J]. 天津大学学报（社会科学版）， 2013（3）： 193197.

[21]杨仕辉， 孔珍珠， 杨景茜. 碳补贴政策下低碳供应链企业一体化策略分析[J]. 產经评论， 2016（6）： 2738.

[22]崔连标， 朱磊， 范英. 碳关税背景下中国主动减排策略可行性分析[J]. 管理科学， 2013（1）： 101111.

[23]孙夙鹏， 孙晓阳. 低碳经济下环境NGO参与企业碳减排的演化博弈分析[J]. 运筹与管理， 2016（2）： 113119.

[24]李友东， 赵道致， 夏良杰. 低碳供应链环境下政府和核心企业的演化博弈模型[J]. 统计与决策， 2013（20）： 3841.

[25]张国兴， 张绪涛， 程素杰， 等. 节能减排补贴政策下的企业与政府信号博弈模型[J]. 中国管理科学， 2013（4）： 129136.

[26]Nagarajan M， Sosic G. Game theoretic analysis of cooperation among supply chain agents： Review and extensions[J]. European Journal of Operational Research， 2008， 187（3）： 719745.

[27]Nash J. Non cooperative games[J]. Annals of Mathematics （Second Series）， 1951， 54（2）： 286295.

[28]田盈， 蒲勇健. 上游企业R&D投资策略的博弈分析[J]. 中国管理科学， 2004（4）： 2832.

[29]Subramanian R， Gupta S， Talbot B. Compliance strategies under permits for emissions[J]. Production and Operations Management， 2007， 16（6）： 763779.

[30]Bergson A. A reformulation of certain aspects of welfare economics[J]. The Quarterly Journal of Economics， 1938， 52（2）： 310334.

[31]于维生. 博弈论与经济[M]. 北京： 高等教育出版社， 2007： 2223.

[32]Smith J M， Price G R. The logic of animal conflict[J]. Nature， 1973， 246（5427）： 1518.

[33]Friedman D. Evolutionary games in economics[J]. Econometrica， 1991， 59（3）： 637666.

[34]张良桥. 进化稳定均衡与纳什均衡——兼谈进化博弈理论的发展[J]. 经济科学， 2001（3）： 103111.

责任编辑、校对： 高原

Research on Government Enterprise Game in Green Supply Chain under the Background of Low Carbon Economy

—Based on the Target of Enterprise Independent Emission Reduction

TANG Huiling

（School of Accountancy， Shanghai University of Finance and Economics， Shanghai 200433， China）

Abstract：Using the Nash equilibrium theory and Evolutionary game theory， this paper studies the behavior game of government and enterprise on emission reduction in the green supply chain. Firstly， according to the government’s function of serving the public， the government’s objective function is innovatively represented by social welfare function and the Nash equilibrium strategy of the government enterprise game is solved as （supervision， low carbon production）. Establishment conditions of Nash equilibrium are given for reasonable economic explanations. After considering the incomplete rationality of game participants in the actual situation， the government objective function is modified. The process of the government enterprise game is described by using a two population evolutionary game， then the evolutionary stabilization strategies under four different conditions are analyzed， and are endowed by economic implications. Finally， the differences between the two game analysis are compared; the policy suggestions are put forward from the perspective of government， enterprises and consumers based on the game equilibrium strategies calculated. This study reveals that only when the government， enterprises and the public work together can the goal of strict government supervision and enterprises’ independent emission reduction be achieved.

Keywords：Game between government and enterprises; Low carbon economy; Green supply chain; Consumer preferences; Social welfare; Enterprise emission reduction; Nash equilibrium; Evolutionary game theory