直线定比分割在建筑制图中的应用研究

肖昕迪 袁玲

摘要：有节奏变化构件的建筑施工图和透视图手工绘制时，构件尺寸定量需要反复操作，过程较为繁琐，但是采用直线定比分割的方法绘制，事半功倍.本文从直线定比分割理论着手，介绍了其在建筑施工图和透视图中的应用方法，以及比值为无理数时的应用方法.

关键词：定比分割;建筑制图;楼梯施工图;透视图

中图分类号：O185.2  文献标识码：A  文章编号：1673-260X（2019）07-0020-03

建筑图样是建筑工程行业交流的必需工具，在其它相关领域中也有着非常广泛的应用.随着计算机绘图软件的发展，计算机取代了大部分的手工制图内容，但手工制图在绘制效果图、透视图、以及小项目施工图时，更为快捷.尤其是对于初学者来说，手工制图入门较低，更容易掌握图样中的相关标注和规定，在其表达方案时更简单快捷[1]，也是计算机制图的必需基础[2].另外，设计人员构思和方案交流时，手工制图使思维和手眼之间以白纸黑线条的效果呈现得更流畅，操作也更为灵活[3].然而，手工绘图时常常遇到较为繁琐的、难以控制的尺寸定量绘制，如楼梯台阶等有节奏变化形体的施工图、透视图.直线定比分割在数学领域中是个较为简单的基础解题方法，对建筑制图中，对有节奏变化形体的施工图和透视效果图采用直线定比分割的方法，事半功倍.

1 直线定比分割理论

如图1，五等分直线AB，需以直线端点A或者端点B为顶点，做一条射线.在射线上从顶点位置起，取五等份，并依次编注各分点：1、2、3、4、5，连接B5.然后过其他分点分别做直线平行B5，形成平行直线组，并交AB于四个点，即为所求[4].

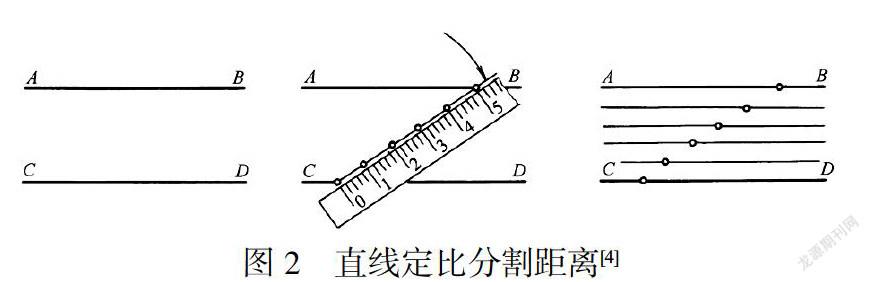
平面图形中的距离等分也可以用此方法，如下图2图中的两平行线之间的距离等分.放直尺于两线之间，按等分份数来选择其整倍数的刻度，并画出一直线做等分，取得各分点后，过个分点作两直线的平行线，即把两平行线间距离等分.

这种等分两平行线间距离的方法，在建筑施工图中可运用于楼梯平面图、剖面图的作图中.

2 在建筑施工图中应用

在绘制建筑施工图中的楼梯平面图和剖面图时，操作工序较琐碎，图样绘制较耗时，每个台阶都需要逐一定位后方可绘制.如果才用直线定比分割的办法，事半功倍.如图3，定位每个踏步时，只需要等比分割楼梯段的长度L即可.

除此之外，还有在楼梯立面图绘制时的应用.在绘制每个台阶时，可先定位高度方向.如图4所示，把楼梯高度分段为L1、L2，分别对L1、L2进行等比分割，取得各分点后做定位轴线B、D轴的平行线;再把楼梯段的水平长度M做定比分割，取得各分点后做平行直线组.此两种方向各平行直线组相交即得出楼梯台阶位置图，再按照相关国标规定绘制图例和标注，即绘制出楼梯剖面图.

3 在透视图中的应用

在透视图中，除画面上的图形元素，其他与实际形状和正投影形成的视图相比，都发生了不同程度的变形.在手工制图时准确、快速地绘出各元素的透视一直图学界探讨的问题.下面以楼梯台阶的透视图为例，以直线定比分割来探讨其简捷的绘制方法.

3.1 透视图中直线定比分割的可行性

由图1、图2、图3、图4可知，直线的定比分割在绘制构件的投影视图中较为快捷，主要通过辅助射线上的分点做平行直线组的方法交于被分割的直線上来取得各分点.辅助射线与被分割直线的关联为连接二者分点之间的平行直线组，而这些平行直线组中的各直线必平行.透视图中，相互平行的直线共灭点[5][6].如图5，分割直线AB为2：3，其分线BB1∥CC1，则透视图中，BOBO1与COC1O有共同的灭点F.由于AB1与AB分点之间的连线在空间中互相平行，在透视图中共灭点，在透视图中可按分线共灭点的方法进行定比分割.

3.2 透视图中直线定比分割的应用

例如楼梯的两点透视图的绘制，对于各台阶的透视定位，如果逐一求解各个台阶上直线节点，不仅工作量巨大，辅助线也会增多，最终将会因作图线条过多导致无法完成完整的透视图.但是采用直线定比分割的办法，分割台阶梯段高度Cc透视和斜线Ac透视，将会把作图过程简化.如图6.其过程如下：

（1）按照透视图的求解方法，求出AC的透视AOCO和基透视AOco.

（2）以图1的方法在空间中分割Ac五等份.此时做的射线A5必须在画面上或者为基线平行线.取得分点后，利用“相互平行的直线共灭点”、以及“基面上的线透视灭点在视平线上”[5][6]的理论，如图5的做法，推理出5co的灭点F即为AOco与Ao5分点5条连线的灭点，由此可在透视图（图6）中分割AOco.

（3）由F点连接Ao5上的各分点，交于AOco上四点，这四个点即为Ac线段上的五分点的透视.由此四分点的透视做铅垂线交于AOCO，即求出AC的五等分点的透视.

（4）由于Cc是平行于画面的铅垂线，“画面平行线的透视与其本身平行，且成比例”[4]，Coco的等分可直接采用图1的方法进行分割，并得出四个等分点.

（5）由Coco的等分点连接灭点FX并反向延长，分别与AOCO的各分点透视相交，即能绘出AC间个台阶的透视图.再以F灭点连接各台阶折点，即能完整绘出台阶的透视图.

4 比值为无理数的应用

以上的内容都是在对线段整数分割时较为有利，对于比值为无理数分割时，就很难按这些方法操作，但可以构建直角三角形，采用比例转移的方法进行分割.如图7，水平圆的透视作图.

对于圆的透视图和轴测图建筑制图中常常采用的画法为“八点法”，即通过求解圆周上八个点的投影位置，来定圆的投影形状.此八点分别为圆外接正方形上的四个切点、外接正方形对角线与圆周的四个交点，如图7.

从视图中可知，四个切点1、2、3、4的位置均在正方形四个边的中点上，在透视图中，由于直线24平行于画面，可过对角线交点做平行于基线OX的平行线和过对角线交点连接灭点M的方法，分别交于四边1o、2o、3o、4o，即为1、2、3、4点的透视.

视图中的另外5、6、7、8四个点位于各段对角线1：的分点处，可通过在直线1B上构建等腰直角三角形的方法来分割.具体作图过程为：以1点为圆心，以直角边长为半径画弧交出BD点，过B点做直线平行于正方形左侧边，交于对角线上的7、8点.右侧5、6点与7、8点可直接对称绘制出即可.由于直线56、78与两侧边平行，在透视图中共灭点.由于直线AB在画面上且与基线重合，其上的分割比例不发生改变，所以可直接以1B所在半段边长、1A所在半段边长构建等腰直角三角形，分割出1：的分点，过分点作直线连接正方的的灭点，与对角线的交点即为5o、6o、7o、8o.如此，八个点的透视均已求出，按顺序用光滑的曲线连接即可求出圆的透视.

5 总结

本文基于直线定比分割方法分析了在建筑图样应用的三种情况，在绘制定比变化的形体图样时较为快捷，使复杂的楼梯平、剖面图绘制过程简单化.并针对透视图中对直线分割的应用做了探讨，另分析了直线分割比值为无理数时，采用构建直角三角形的方法转移比例的应用技巧.

参考文献：

〔1〕于习法，易素君，孙霞，张莉.两点透视图的一种画法和透视图尺设计的研究[J].工程图学学报，2008（05）：121-124.

〔2〕张学炯.机械手工制图准备及错误分析[J].科技视界，2019（03）：132-133.

〔3〕邱冰，张帆.以理想角度作两点透视图的一种简画法[J].图学学报，2012，33（06）：140-145.

〔4〕何斌，陈锦昌，陈炽坤.建筑制图[M].北京：高等教育出版社，2005.

〔5〕邓学雄，江晓红，等.建筑图学[M].北京：高等教育出版社，2015.

〔6〕吴机际.园林工程制图[M].广州：华南理工大学出版社，2016.