一个效率函数的极值原理及其解释应用
2019-09-10邓志雄


1 一个效率函数的极值原理
2 效率函数极值原理解释应用的三个案例
效率函数的极值原理在现实经济社会生活中具有广泛的解释应用能力,只要相关经济社会现象满足这个函数的变量关系及其要求的极值条件即可。下面,笔者就应用效率函数的极值原理,分别从宏观、中观、微观层面各列举一个案例来做出分析解释。
2.1 宏观案例——社会资源总体配置效率提升问题
每个国家的社会资源都要经由国家与私人两个部门来共同配置。因此,社会资源配置过程总体上可以理解为分两大步完成:国家宏观配置与私人微观配置。宏观和微观的先后秩序在不同国家、不同体制、不同文化下会有所不同,同一国家不同性质的社会资源的配置秩序也各有不同,但这些并不影响我们在总体上将社会资源配置分为宏观与微观两大步完成的判断和分析。
假设国家宏观配置资源的效率为x,私人微观配置资源的效率为y,那么,S=xy,即两步的配置效率之乘积是一个表征社会资源总体配置效率的函数。这个乘积越大,标志着社会资源总体配置效率越高。当这个乘积达到最大,社会资源的总体配置效率就达到最高。在一定时期比如一个季度或一个年度内,由于国家和私人资源配置效率x和y的变化都很小,以至于其变化可以被忽略不计,这使得x与y之和也可被视为保持定值不变,即函数S=xy满足x>0、y>0,且x+y=c,c为常数的条件。按照上述效率函数的极值原理,社会资源总体配置效率S=xy将在x=y时取得最大值。
这就说明,当且仅当国家与私人两者的资源配置效率彼此均衡时,社会资源总体配置效率才能实现最大化。因此,各种经济体都应尽力争取均衡提升国家和个人两方面参与社会资源配置的积极性和配置效率,不应厚此薄彼,不可有所偏颇,不必主观好恶。市场失序造成的混乱和社会僵化带来的低效,政府过大产生的低效和政府过小造成的能力缺失,都无益于社会资源配置效率的提高。
美国的私有经济很发达,企业配置资源效率很高;同时,凭借超级大国和强势美元的地位,美国的国家配置资源能力也全球无敌,二者共同支撑了美国经济在全球市场的高效运行。然而,美国在华盛顿共识下向北美、俄罗斯、东欧、中东和非洲等地输出的国家经济改革方案,却都毫无例外地片面强调给予私人配置资源的便利,却极端削弱政府资源配置能力,结果使这些国家的经济在改革中因失去国家与私人在资源配置效率上的均衡,普遍出现了转型失败。普京在俄罗斯执政后,逐步重振国有经济,使俄罗斯国家资源配置能力与私人资源配置能力开始趋向均衡,从而促使俄罗斯经济重新得到了增长。从中,我们可以从正反两方面看出效率函数S=xy极值原理的深刻效应。
中国的经济发展历史更是这样。旧时的中国四分五裂,几乎没有国有经济,国民经济宛如一盘散沙,社会整体资源配置效率很低。新中国在实行计划经济时期,只注重政府对资源的配置效率,私人配置资源的约束强、效率低,社会经济发展相对较慢。改革开放以来,中国坚持以公有制为主体、多种所有制并存的基本经济制度,毫不动摇地巩固发展公有经济,毫不动摇地引导支持非公经济发展,大力发展混合所有制经济,不断推进社会主义市场经济体制建设,既注重发挥市场在资源配置中的决定性作用,又强调更好地发挥政府作用,国家和私人的资源配置效率均衡提升,公有经济和私有经济都得到很大发展,综合国力大为提高,对世界的贡献也不断扩大。因此,可以说,在社会资源配置上坚持按效率函数S=xy的极值原理办事,始终注重均衡发挥国家和个人两个积极性,正是中国改革发展的独特经验。
世界各国的发展实践表明,只要公有制经济,不要私有制和混合所有制经济,就不能充分调动广大群众的积极性,经济发展就缺乏资本和效率,会出现发展不足的问题。这相当于图1中(x,y)点往X轴移动,偏离直线中点后导致S面积逐渐缩小。只要私有制,不要公有制,经济社会就会因两极分化而陷于不公平不稳定的混乱状态,导致资源配置效率下降,从而出现发展不当的问题。这相当于图1中(x,y)点向Y轴运动,偏离中点后也导致S面积缩小。强调坚持公有制,鼓励私有制,但不大力推进公有和非公有资本交叉持股、相互融合的混合所有制,经济社会就会陷入彼此孤立、相互排斥、缺少合作、丧失和谐的不良状态,会出现此进彼退、争吵不断、发展不稳的问题,不利于社会总体资源配置效率的进一步提高。这在图1中相当于在较长时期内c=x+y直线存在向内收缩的危险、失去向外扩张的能力,不能实现每隔一段时间就跃上一个新的台阶,从而妨碍S的一步步提高。
因此,我们必須既坚持两个毫不动摇,又大力发展混合所有制经济,把公有制、私有制和混合所有制都视为社会主义初级阶段基本经济制度的重要实现形式。当前,我们特别要将加快包括国资控股企业和国资参股企业在内的混合所有制企业的发展作为提升经济效率的重点工作,尽快将混合所有制企业与国有企业分开监管,使混合所有制企业获得更好的市场化运营效率。未来,我们应该按照S=xy效率函数极值原理所揭示的规律,通过大力发展混合所有制经济,扩大国有经济和私有经济的投资发展空间,克服彼此的短板,弘扬双方优势,形成改革发展的更大合力,不断提升全社会资源配置效率,通过“执两用中”,促进“三生万物”,实现稳中求进,确保中国经济持续有效地实现高质量发展。
2.2 中观案例——企业制度演变问题
办企业需要资本,做企业需要人本。资本与人本两合是企业发展的客观要求,企业制度建设要均衡考虑人合与资合两大因素。在市场经济条件下,企业将本求利,其发展先要有资本投入形成产能,后要靠员工劳动创造良品。在一定时期内,比如一个季度或者一个年度,企业中资本运行效率与员工劳动效率x和y均为正值,且两者之和x+y可视为一个定量,因此,企业资源配置总体效率S=xy满足效率函数的极值条件,企业运行效率将在资本运行效率与员工劳动效率均衡时实现最大化。
这就告诉我们,企业运作既要有良好的资本运行效率,也要有较高的劳动生产效率,既要投得好,也要干得好,企业才有竞争力。不能只强调资本运行效率,再好的生产线也不会自动产出良品;也不能只强调员工劳动效率,生产线技术水平必然制约劳动效率的发挥。因此,每个企业都需要高度关注资本运行效率与员工劳动效率的均衡。
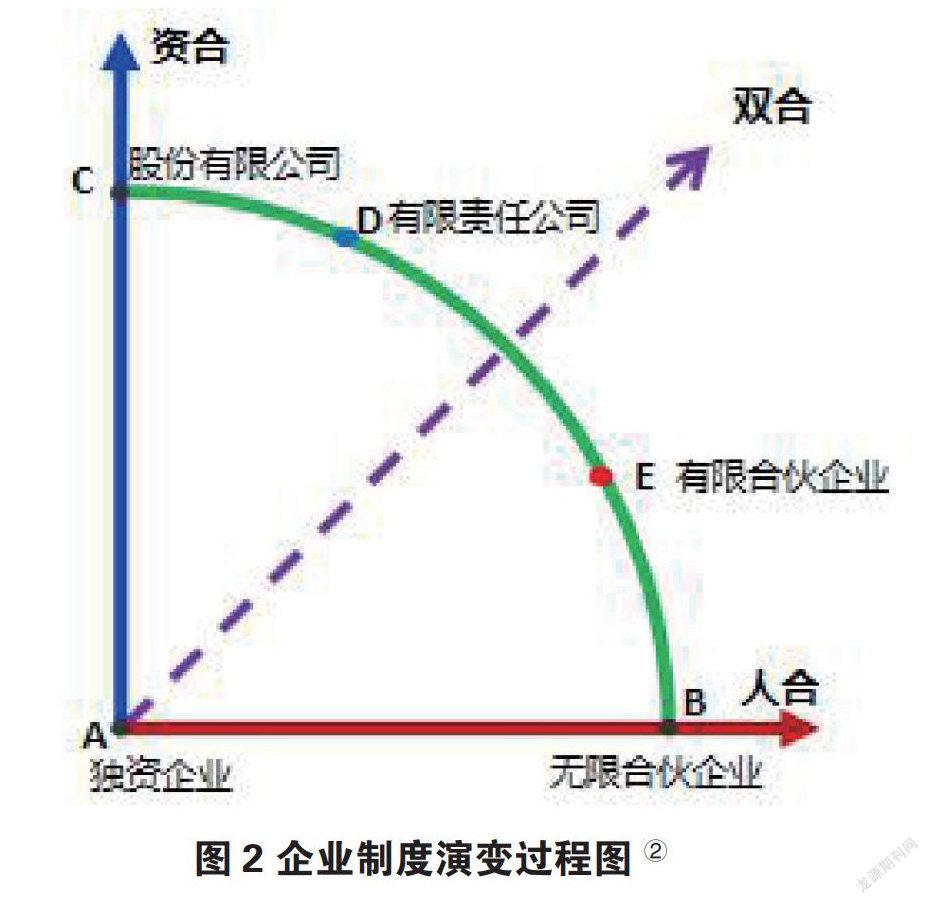
企业制度演变的历程也反映了这一原理的长期作用和未来取向。企业制度演变的逻辑在于资本和人本的关系随生产力变化而变化。企业发展需要资本和人本两方面的合力。因此,人本与资本更好地实现双合的机制设计是企业制度的灵魂。在生产力发展的不同时代,人合与资合有着不同的价值,因此导致不同时代的企业制度对人合与资合会有不同偏重。如图2所示,企业制度随生产力发展的演变过程,具有资合与人合两合不断增强的内在逻辑。
历史上,世界各国先后出现了五种得到普遍应用的企业制度。最初,在农业社会,社会生产力主要是人的体力,对应出现的企业当然是独资企业,各家举一人一户之资力创业发展。之后,为增强生产能力,加快企业发展,亲朋好友相邀入伙,共同经营,有利同享,有责共担,产生了纯粹人合的无限合伙企业。当工业革命来临,企业生产经营规模迅速扩大,机器成为主要的生产力,需要大资本支持大生产并抗衡大风险时,上市面向公众筹资的纯粹资合的股份公司便被创设出来。当工业革命创造的社会资本大量集中于机构投资者而非散户手中之后,向少量机构投资者私募融资就能满足企业资本形成的需要,股东较少的以资合兼顾人合的有限责任公司便如雨后春笋般产生出来。到了后工业时代,创新引领发展,人的脑力成为最重要的生产力,人本价值大幅提升,以人合为主兼顾资合的有限合伙企业便加快发展起来。面向未来,十分明显的趋势是,科技文化产业将引领社会经济发展,双合力量均衡强大的平台+小微形态的混合所有制企业将成为社会上的主导企业制度。
2.3 微观案例——企业管理中的集权分权问题
常识告诉人们:科学的分工提高劳动效率、恰当的分权提高管理效率、必要的分利提高协同效率。现在,我们可以用效率函数的机制原理来解释组织中分权提升管理效率等这类常识或常见现象。
任何母子公司结构的企业都面临适度集权与分权的管理需求。权力过分集中于总部,有利于强化企业整体运行控制,但不利于子公司根据市场变化自主经营。权力下放基层,有利于增强子公司经营活力,更好地适应市场发展需要,但会对集团总体风控与平衡发展带来挑战。因此,企业需要适度的集权分权,于是带来需要把握好总部和子公司管理效率提升的均衡性问题。
如果把企业管理中的权力视作一种资源,企业管理中的集权分权问题也就是一个资源配置问题。我们把企业管理权划分为总部管理权和子公司管理权,设二者的管理效率分别为x和y,则企业整体管理效率S=xy。由于在一定時期比如一周、一月或一个季度内企业总部和子公司的管理效率变化不大,可以认定函数S=xy满足x>0、y>0,且x+y=c,c为定值的条件。因此,根据效率函数S=xy的极值原理,企业的整体管理效率将在总部和子公司管理效率对等时取得最大值。
这就告诉我们,在母子公司的企业管理过程中,不进行正确的集权分权,片面追求总部管理效率最高或单方面强调子公司提高经营自主权,都是不正确的,都会损害企业集团的整体管理效率。要提升企业管理整体效率,必须注重总部集中管理和子公司自主经营的相互均衡,并通过优化集权分权、完善管理制度、调整管理者、提升员工执行力等,努力争取每隔一段时间就有一个c=x+y的整体跃升,不断提高企业管理总体效率。
3 其它应用展望
执两用中,适为常道。显然,对于社会年度产出用于积累与消费实现的经济增长效率、社会资本在金融领域和实体产业中分配的总体配置效率、企业增加值用于劳动工资与资本报酬形成的激励效率、平台企业与小微实体通过利润分享达成的协同发展效率、基础设施建设与运营服务的总体效率提升等众多与双因素效率函数相关的经济问题,我们都可以做出与上述三个案例类似的分析与解释。因为它们都基本满足S=xy的函数关系,又都满足在一定时期内两个变量的贡献为正且二者之和为定值的极值条件。相信读者们也可以轻松地从工作与生活中举出更多例子,展开相应的分析与解释,并受益于效率函数极值原理揭示的道理,学会既一分为二、又合二为一的看世界、干事业。
(作者为中央企业专职外部董事、国务院国资委产权局原局长、规划发展局原局长)
注释:
①杨胡凤作
②参见邓志雄等著:《岭峰之观》
