“角的初步认识和大小比较”教学设计与评析
2019-09-10王君畬卢艳唐剑岚
王君畬 卢艳 唐剑岚
【摘 要】“角的初步认识”是北师大版小学数学二年级下册的重点内容,其中角的特征概括与大小比较是教学的重难点。传统教学通过让学生触摸角的模型,进而感知角的特征和大小,但模型的难以变化性,阻碍了学生全面理解角的特征和找到比较角大小的思路。文章试图探讨如何运用Hawgent皓骏动态数学技术优化“认识角”的概念教学,以期为提高小学数学图形与几何概念教学提供一定的参考。
【关键词】角的大小;Hawgent皓骏;小学数学
“角的初步认识”一课出自北师大版小学数学二年级下册 “认识角”的内容,是图形与几何的重要基础内容,也是该学段的重点内容,其中角的特征与大小比较是教学的重难点。传统教学常常借助角的模型让学生摸一摸、看一看、说一说,以帮助学生感知角的特征和大小。但由于模型本身具有不可变的局限,难以帮助学生从模型中抽象出角的概念,也难以促进学生全面理解角的特征和找到比较角大小的思路。针对上述教学的重难点,本文试图探讨如何运用Hawgent皓骏动态数学技术优化教学设计,在突出重点和破解难点的同时,实现“授人以渔与欲”[1]。
首先,设计“画一画,说一说”环节。学生画角之后,教师分别动态呈现“射线画角”和“旋转画角”的过程,并要求学生说一说角的特征。其次,设计“看一看,说一说”环节,再次动态展示“射线画角”和“旋转画角”的过程,引导学生仔细观察角的变化过程,并再次让学生说一说“角长什么样”。最后,设计“想一想,说一说”环节,通过问题链,动态演示比较角大小的方法,即将其中一个角拖动至另一个角处,使它们的顶点及一条边重叠;动态演示拉长或缩短角的边但角大小不变的情境。根据上述的创课思路,研究者进行了“角的初步认识和大小比较”概念教学的创课。
1.画一画,说一说
师:前面已经呈现了很多存在于我们身边的角,你们知道角长什么样了吗?请画出你们心中的角。
(学生动手画角,教师走到学生中观察)
师:有的学生先画一个点,然后将三角板的尖对准这个点,再从这个点出发,沿着三角板的两条边画线。还有的学生也是先画一个点,然后从这个点出发,用尺子画两条线。(教师运用Hawgent皓骏动态数学技术画角)
2.看一看,说一说
师:大家都做得非常棒,画出的这些都是角。请观察所画的角,你们知道到底什么是角了吗?
生1:角是由一个点和两条线组成的图形。
师:很好,这个点我们称它为角的顶点,两条线叫角的边,角是由一个顶点和两条边组成的图形。很多学生在画角的两条边时都会借用尺子,这说明大家都观察到了角的两条边都是直线。那像这样由两条弯曲的边构成的图形就不是角。(讲解过程中闪动角的各部分)
3.想一想,说一说
师:那么应该如何比较它们的大小呢?
生2:角的两条边张口大,角就大;角的两条边张口小,角就小。
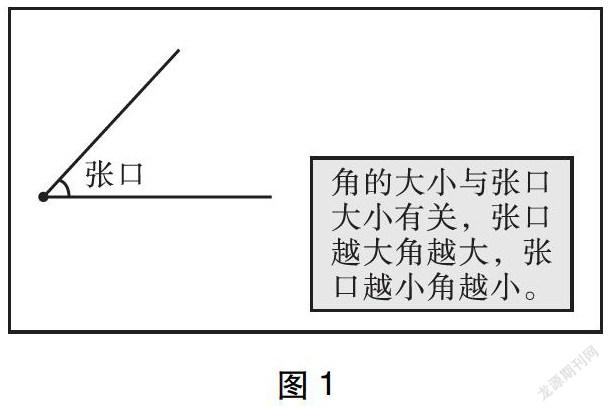
师:很好!当旋转角的一条边时,张口大小就改变了(旋转角的一边,角越来越大)。现在我们可以很清楚地看到角的大小与张口大小有关,张口越大角越大,张口越小角越小(同步旋转角的一条边,如图1所示)。
師:现在有一个红角和一个蓝角(如图2所示),你们能比较出哪个角大,哪个角小吗?

生3:我觉得蓝角大,因为蓝角的边比较长。
生4:不对,角的大小不是这样比较的。
师:看来生4有不同的看法。请你说说如何比较角的大小?
生4:我认为角的大小和角两条边的张口大小有关。比较角的大小,要看两条边张口的大小,可以把两个角放在一起比较。将蓝角的顶点移动到红角的顶点处,使蓝角的一条边与红角的一条边重叠。如果两个角的两条边张口一样大,说明两个角一样大(拖动蓝角,使其顶点和一条边与红角重叠)。
师:蓝角和红角的两条边完全重合,所以两个角一样大!原来角的大小与两条边的长度没有关系,只与两条边的张口大小有关。我们用一个口诀来总结本节课学过的知识:我是一个小小角,一个顶点两条边,想知我的大与小,要看张口不看边。
本节课要重点突破两个难点,一是帮助学生建立角的概念,二是纠正学生对角大小的认识偏差。鉴于二年级学生以形象思维为主,难以概括角的本质特征和比较角的大小,因此教师以画角为新知识学习的逻辑起点,让学生经历三个环节认识角,直观感知角的形状和组成元素,从而抽象出角的概念。
对于比较角的大小,教师先提问学生角的大小与什么有关,从而引发学生认知冲突,接着动态呈现“角的大小只与角两条边张口的大小有关”的情境,最后用口诀小结比较角大小的方法,达到“授人以鱼的同时授人渔与欲”[2]的目的。
在这个教学过程中,教师应根据学情,提高活动环节的质量,调整其顺序,直到大多数学生能抽象出角的概念,理解判断角大小的方法。
参考文献:
[1]唐剑岚,周元.“授人以鱼”的同时“授人以渔与欲”:以《等差数列的前n项和》公式推导片段为例[J].数学通报,2016(9):41-46.
[2]唐剑岚,陈圆.基于“鱼渔欲”三位一体优化教学理念的数学创课设计:以“一次函数的图象与性质”的教学为例[J].中小学课堂教学研究,2017(12):34-37.
