数学画图“画”在何处？

陈娇娇

摘 要：随着《义务教育数学课程标准（2011版）》的出台，一线教师越来越重视数学思想与方法的培养。在数学教学中能让学生自主地应用画图策略解题，把问题呈现的信息“画”出来，但对于“画”在什么地方才合适呢？却思考不多。本文将从画在“思维困难”处—理清关系、画在“思维困惑”处—拓宽思路、画在“思维发散”处—发展能力三大方面进行论述。

关键词：画图策略;数学思维;作用

数学期末测试结束了，笔者拿到测试卷，仔细翻阅学生的卷子，试卷有这样一道题：林芳买了一张1平方米的大正方形纸，她折一只纸鹤需要用边长2分米的正方形纸，这张大正方形纸最多可以折多少只纸鹤？对于这道充满实践性和探索性的题目，学生做题情况会是如何呢？笔者发现大部分孩子能利用画图来解题，从图中可以看出学生具有初步的“画图解题”技能，更可以看出学生解题思路很清晰。（如下图）这样的结果出乎笔者的意料，但又在情理之中。三年来，笔者在执教的班级一直尝试着“画数学”的教学，尝试让学生慢慢地将“画”深刻在脑海中，难以理解时“画”，产生困惑时“画”，无从下手时更要“画”。教师在教学中有必要渗透学生的“画图”意识，这样能让学生在解题时“山穷水尽”又“柳暗花明”。但在什么时候画才能落到实处，避免流于形式呢？笔者结合自身教学的所思所想，谈谈自己的见解。

一、画在“思维困难”处，理清关系

苏霍姆林斯基说：“如果哪个孩子学会了画应用题，我就可以有把握地说，他一定能学会解应用题。”换种说法，儿童天生就喜欢涂鸦，他们总喜欢用图画表达自己的想法。教师可巧借这天性来帮助他们学数学，有意识地引导学生在解题思路不清晰的情路况下尝试画图，将抽象的数学信息转化为有形的图式，理顺复杂问题中的数量关系。这样，抽象的数学语言就变得简单、明了，清晰易懂了[1]。例如：教学“叶老师、小玲家、学校在同一条路上。叶老师家离学校672米，小玲家离学校250米。叶老师家离小玲家有多远？有几种情况？”时，由于学生的年龄小，生活经验有限，再加上空间想像能力不足，绝大多数的学生都被这一长串的“离”搞晕了，结果是他们难以用语言将解题思路说出，甚至有一小部分的学生不理解题目意思直接放空。该怎么办呢？研究表明，每个学生都有分析问题、解决问题和创造的潜能。那么，如何抓住学生的“最近发展区”，引导他们主动探索呢？这时教师适时跳出来，鼓励、引导学生：“能不能试着用一种比较简单的方式，将叶老师、小玲家和学校在同一条路上的情况表示出来？”于是有一大半的学生都想到了“画”。通过画，理清了三者间的关系，把抽象的文字语言变成直观的图形，叶老师到小玲家的距离有2种情况：在学校的同一侧，在学校的两侧。这样学生通过“跳一跳”就能摘到“果子”，理清思路，难题也就迎刃而解了。（如下图）通过画图的方法，使学生在思维困难处，能从抽象到直观，让形象思维与抽象思维和谐共舞。这样的过程，学生学得轻松又快乐，化复杂为简单，很快就找到解决问题的方法。这样的过程，相信学生对知识的理解和掌握是更为深刻的。

二、画在“思维转折”处，拓宽思路

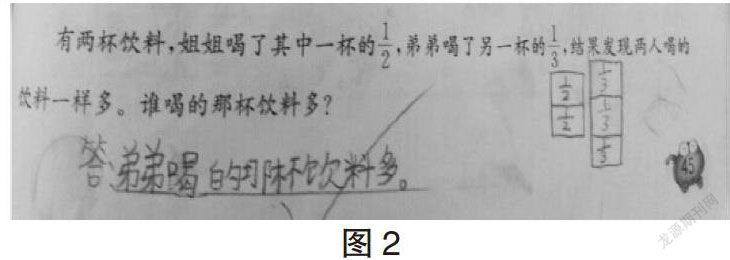
在数学王国里，最难的就是把文字信息准确转化为数学语言。数学家华罗庚先生说“数无形时不直观，形无数时难入微”，而波利亚也曾说过：“抽象的道理是重要的，但要用一切办法使他们看得见、摸得着。”而“画图”就是一个很好的载体。教师可巧借这载体，引导学生在思维转折处画，帮助他们拓宽思路较好地解决问题。[2]例如：教学“有两杯饮料，姐姐喝了其中一杯的，弟弟喝了另外的，结果发现两人喝的饮料一样多，谁喝的那杯饮料多？”时，理解“喝的饮料”和“剩下的饮料”这两部分之间的关系是这道题的关键，但对刚接触分数的他们来说却是一大难点，是他们思维容易产生困惑的地方，有一部分学生直接利用分数的大小来进行比较，“因为>，所以弟弟剩下的多。”可在课堂上笔者也发现有相当一部分学生因为>，结果却是姐姐的饮料多。从实例中可以看出，学生的困惑出就在于和的一份，如果能把抽象的文字转化成生动的图画，看着图进行思考，难度就大大降低了。笔者顺势一带：“要是能把这和画出来，那……”在教师的启发下，学生对画图有了强烈的认知需求，纷纷动笔画、想，最后在“看图”思考中有了重大的发现“这一份必须相等。”学生在交流中解决了自己的困惑，在观察、比较中得出正确答案，即知其然，又知其所以然。（如图1）又例如：教学“两个一样大小的长方形，长都是10厘米，宽都是5厘米，拼成一个正方形或者长方形，周长和面积各是多少？”时，由于三年段的学生空间想像能力较差，如果让他们直接在头脑中建构图形然后直接计算，有些困难。针对这一问题，笔者采取分步教学，先让学生利用学具摆2个长方形，直观感受拼摆后的新图形。在学生有了实际操作的经验基础上，笔者话锋一转，引导学生思考“那如果没有实物或平面图形让你拼摆，该怎么办呢？”稍加沉默后，学生纷纷想到了“不能摆，那就画出来”。在“画”中学生顿悟到大长方形的长、宽和原来的小长方形的长、宽之间的关系，这样的深刻顿悟是在“画”的基础上产生的，没有“画”，理解是浅显的，没有“画”，语言是苍白的。（如图2）只有“画”在学生的思维困惑处，通过用图想事，借图促思，据图说理，才能把抽象的数学语言化成形象的图形、语言，从而帮助学生思考、探索，突破学习瓶颈，提升解决问题的能力。

三、画在“思维发散”处，发展能力

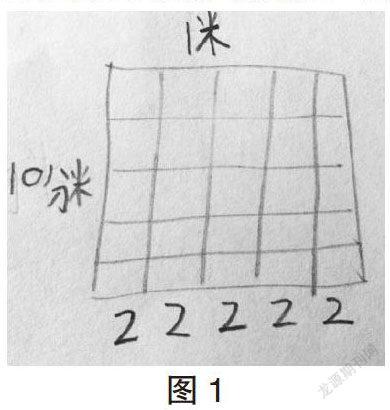
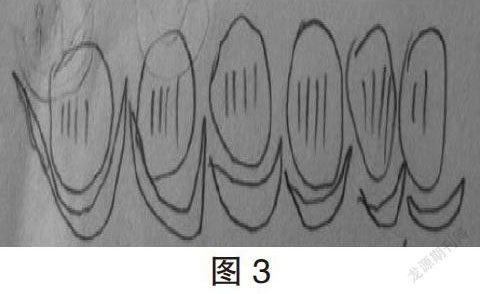
数学家罗素说：“什么是数学？数学就是符号加逻辑。”《义务教育数学课程标准（2011版）》把发展学生的符号意识作为重要的学习内容，强调建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。因此，学生的符号意识的建立能发散学生的逻辑思维。[3]例如：在教学《有余数除法的解决问题》中，笔者是这样处理的。出示主题图，让生从图中找到信息和问题后：有22人去划船，每条船最多坐4人，至少需要几条船？笔者试着让学生大胆讨论可以用什么方法来试着解决“他们至少要租多少条船？”这个问题。学生各抒己见：摆一摆、画一画、算一算……在学生都有了想法的基础上，笔者大胆放手让学生自己动手解决“他们至少要租多少条船”这个问题。学生有的用学具摆一摆，有的画一画，还有些则是动笔算一算，都用了自己所喜欢的方式来解决这道题。汇报时，笔者有意识地将收集到的作品分层次呈现，再引导学生对比，在对比中优化画图策略，解决问题。（如下图）在孩子稚嫩的“画”中，我们可以看到画图的不同形式，有“О”、“〡”、还有可爱的简笔画小船，学生的思维象插上想像的翅膀，不断发散自己的思维，他们在“画图”、“看图”、“想图”的过程中融入自己的靈感、顿悟：“剩下的2人，该怎么办呢？”他们积极思考主动寻找解决问题的策略，在与同学的交流中，思维得到扩展，活力得到释放。这时，笔者再结合学生的感悟讲解“进一法”就水到渠成，体验解决问题策略的多样性的教育也就“润物细无声”了。通过这道题不难看出，让学生画图，其实是在有意识地挖掘并唤醒学生的符号意识，架起文字、符号与图形语言之间的桥梁，通过思维的碰撞，让那些显得刻板的文字或符号变成鲜活的图形，让学生在交流中理解，在应用中辨析，在反思中提升，从而有利于释放学生思维的活力，培养学生的创造能力。

总之，“画数学”能画出师生的“新”世界，已经成为教与学的一种方法，成为解决数学问题的一种思想方法。在数学教学中，教师要启发学生在画中思考，看图中探究，在想图中释疑，才能使教师教得简单，学生学得轻松。才能使学生在知识与思维的轨道上更好的交汇融合，达到事半功倍的效果。

参考文献

[1]曹培英.小学数学问题解决的教学研究（四）.小学数学教育，2013，10

[2]《义务教育教科书（教师教学用书）》北京：人民教育出版社，2013：137～141

[3]杨豫晖.义务教育课程标准（2011版）案例式解读（小学数学）.北京：教育科学出版社，2012：42～43

[4]叶建云等.可以这样教数学.上海：华东师范大学出版社，2012：98～111