自然破解难点 积累活动经验
2019-09-10陈云宋佳真唐剑岚
陈云 宋佳真 唐剑岚


【摘 要】“圆的周长”是图形与几何的重要知识点。本知识点有三个教学难点:化曲为直测量圆周长的方法、发现圆周长与直径的关系、圆周长公式的推导。传统教学常常采用“绕绳”“滚动”等动手实验的方法,让学生多次测量圆的周长与直径或直接告知学生。文章基于课程标准中数学基本活动经验和基本思想方法的培养要求,通过活动单导航、提问链导思,借助Hawgent皓骏动态数学技术,自然破解教学难点的同时,帮助学生积累数学基本活动经验和体悟数学基本思想方法,提升教学有效性,为优化圆周长的教学提供一些参考。
【关键词】圆的周长;活动单;提问链;Hawgent皓骏
【作者简介】陈云,广西科技师范学院教育科学学院教师,研究方向为数学教育;宋佳真,广西师范大学数学与统计学院数学教育硕士研究生;唐剑岚(通讯作者),博士,广西师范大学数学与统计学院硕士研究生导师、教授,主要研究方向为数学课程与教学论、数学教育技术。
【基金项目】小学数学重难点知识可视化设计与应用的研究(桂林市B类课题2016B30);动态数学技术的创新研究与应用项目(GXSDHX201706) 一、创课背景与问题
“圆的周长”是人教版数学六年级上册第5单元“圆”第二节的内容,是图形与几何的重要知识点。在此之前,学生学习了应用测量方法获取长方形和正方形的周长计算公式。圆作为一种由曲线围成的图形,与直线围成的图形相比,在形状上有很大不同。曲线图形不能直接被测量,这与学生原有的知识经验产生冲突,如何“化曲为直”成为第一个教学难点。即使应用“绕绳”“滚动”等动手实验方法,学生通过多次测量圆的周长与直径,也很难发现圆的周长与直径的关系,因为数据里面隐藏了圆周率的秘密[1][2],这是第二个教学难点。师生如何类比长方形、正方形周长公式的推导过程发现圆的周长公式,这是第三个教学难点。本文基于《义务教育数学课程标准(2011年版)》中数学基本活动经验和基本思想方法的培养要求,借助Hawgent皓骏动态数学技术,自然破解教学难点的同时,强化学生数学基本活动经验的积累和数学基本思想方法的体悟,提升教学有效性,为优化圆周长的教学提供一些参考。
二、创课设计与实录
《义务教育数学课程标准(2011年版)》指出,基本活动经验是个体在经历了具体的学科活动之后留下的、具有个体特色的内容,既可以是感觉知觉,也可以是经过反省之后形成的经验[3]。本教学设计主要通过活动单导航、提问链导思,促进学生经历“看一看、说一说、验一验”等显性活动,设计“想一想、猜一猜”等隐性活动,借助Hawgent皓骏动态数学技术自然破解教学难点的同时,帮助学生积累数学基本活动经验和体悟数学基本思想方法,努力实现“授人以鱼”的同时实现“授人以渔”和“授人以欲”[4],提升教学有效性。
首先,设计“忆一忆,想一想”活动,动态呈现长方形与正方形的周长公式推导过程,激活学生原有的知识经验,成为学习新知识的生长点。接着,设计“看一看,说一说”活动,通过“圆的周长是否可以直接用直尺量出来?”等提问链追问学生,并联系学生的生活实际,呈现生活中常见的化曲为直的实例,驱动学生联想绕绳、滚动等方法,实现化曲为直的想法。最后,设计“猜一猜,验一验”活动,再次通过提问链和动态呈现数据分析,促进学生类比长方形、正方形周长公式的推导,引导学生观察、发现数据隐藏的圆周率秘密和圆周长的计算公式。根据上述创课思路,设计如下“圆的周长”教学片段。
1忆一忆,想一想
师:同学们,你们还记得怎样计算长方形和正方形的周长吗?(呈现用直尺测量长方形、正方形周长的动画效果)
小圆:用直尺测量长方形的每条边,然后加起来就是长方形的周长了。
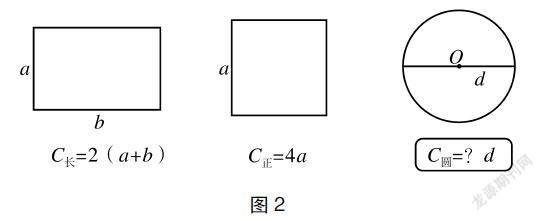
小方:先将长方形和正方形展开成一条线段,再用直尺测量,这条线段就是长方形和正方形的周长了,得到公式C长=2(a+b),C正=4a(动画展开长方形、正方形,闪动长、宽、周长)。
2看一看,说一说
师:这两种方法都是通过直接测量得到的周长。圆是由曲线围成的图形(显示点生成圆的动画),那它的周长是否可以直接用直尺测量出来?如果不能,又有什么办法测量?
小圆:圆的周长好像不能直接用直尺测量出来,怎么办呢?
小方:我们可以将围成圆的曲线变为直线,这样不就可以了吗?
师:小方很有想法!但如何将圆的曲线变为直线呢?其实我们生活中有很多类似的情境,如我们常用的透明胶卷、体育课用的皮尺等(如图1)。看到这些东西,大家有想法了吗?谁来说一说。
小圆:我们可以用一条绳子把圆围一圈,剪掉多余的部分,绳子拉直后测量它的长度,就得到圆的周长了。
(教师同时呈现“绕绳”、绳子展开在直尺上测量的动画效果。)
师:不错的方法,我们常常把这个方法叫做绕绳法(声音突出)!
小方:我也有一个方法,而且不需要绳子。将圆直接在直尺上滚一圈(标记起始点),也可以得到圆的周长。
(教师同时呈现圆在直尺上滚动测量的动画效果。)
师:很好的方法,小方不用绳子也能得到圆的周长。像这样的方法我们叫做滾动法,但要注意在起始位置做好标记!
师:刚才的这些方法为什么能量出圆的周长?其实就是因为曲线围成的圆与直线段可以相互转化。如果一个圆很大,但绳子不够长,而且圆很难滚动,那该如何计算圆的周长呢?看来我们还是有必要去发现、学习计算圆周长的公式。那么,圆周长的公式是什么?是否与长方形、正方形的周长公式有关系呢?
师:其实圆的周长公式与长方形、正方形的周长公式有很密切的关系。长方形的周长是长与宽(声音强调)的和的2倍,即C长=2(a+b);正方形的周长是边长的4倍,即C正=4a(声音强调)。如图2所示,长方形的周长与它的构成要素——长和宽有关,正方形的周长与它的构成要素边长有关,那么圆的周长与它的构成要素直径或半径是否也有关系?
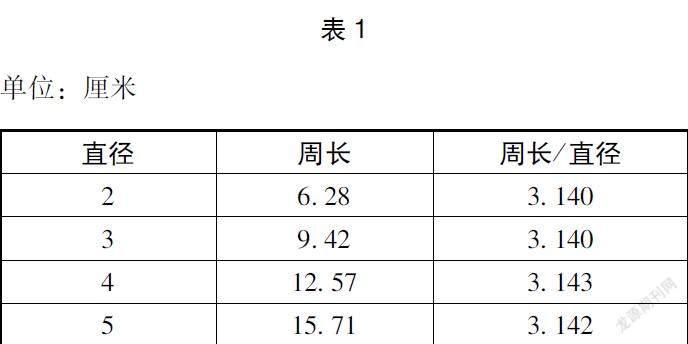
师:我们用刚才的方法来算一算,并列出表1。(教师边说边动态演示用滚动法测量不同半径的圆,得出周长,如图3。)
3猜一猜,验一验
师:观察这个数据表,大家有什么发现,谁来说一说?
小方:我发现半径越大,直径越大,圆越大,圆的周长也越长,所以圆的周长跟它的半径、直径有关。
师:很好,圆的周长跟它的半径、直径有关。谁还能进一步用数据描述圆的周长与直径的数量关系?
师:是否也像长方形和正方形的周长公式一样,与长和宽或边长有倍数关系呢?
小圆:圆的周长与直径好像也有倍数关系。
师:很好的发现,我们输入不同半径的值,看看直径、周长、周长与直径的比值(展示结果,如表1)有什么变化。大家观察表格中圆的周长与直径的数据,发现它们有什么规律?(教师边说边输入任意值,看各组数据的变化。)
小镜:圆的周长与直径的比值都是一个固定的数,它约等于314。
师:真厉害,这就是表格中隐藏的秘密。圆的周长与直径的比值一直都是一个相对固定的数,它约等于314。在数学中,我们把它叫做圆周率,用希腊字母π表示。
师:2300年前,古希腊数学家阿基米德算出了圆的周长大约是直径的314倍多一些。1700年前,我国魏晋时期的数学家刘徽用“割圆术”计算圆的周长大约是直径的31416倍。在2000年时,科学家用计算机算出了圆周率小数点后14万亿位。(呈现:314159265358979323846264338 3279502884197169399375105820974944592307816406286208998628034825342117067982148086513282 306647093844607550582231……)
师:人类花了2000多年,通过无数科学家的毕生努力,最终达成一个共识——无论是大圆还是小圆,它的周长除以直径都等于一个固定数,即314159……,计算公式是圆周长÷直径=圆周率(314159……),这也就是说圆的周长是直径的π倍。今天我们得出的圆周长公式是:C圆=πd=2πr。
三、创课评析与反思
将“鱼渔欲”三位一体的教学理念结合课程标准理念,再将Hawgent皓骏动态数学技术融入教学中,通过三个活动单导航(忆一忆,想一想→看一看,说一说→猜一猜,验一验)和提问链导思,自然破解教学中的三个难点,强化学生基本活动经验的积累和基本思想方法的体悟,在“授人以鱼”的同时实现授人以“渔与欲”,提升教学有效性。
在破解如何测量圆的周长这一环节,设计了“忆一忆,想一想”活动,通过回顾长方形和正方形周长的两种测量方法,激活学生原有知识与经验的同时,通过提问链“圆是由曲线围成的图形(显示点生成圆的动画),那它的周长是否可以直接用直尺测量出来?如果不能,又有什么办法测量?”激起学生的兴趣和好奇,联想新旧知识之间的联系,找寻测量圆周长的办法。本环节设计在授人以“鱼”的同时具有授人以“欲”的功能。
在破解怎样测量圆的周长这一环节,设计了“看一看,说一说”活动,呈现生活中化曲为直的实例,促使学生类比,自然引导学生说出绕绳法、滚动法等测量圆周长的方法。但绕绳法和滚动法只能测量较小的圆,如何计算所有圆的周长,则需要圆周长的计算公式。本环节设计在授人以“渔”的同时实现了授人以“欲”。
在破解圆周长的公式推导这一环节,设计了“猜一猜,验一验”活动,通过提问链引导学生类比长方形、正方形的周长公式,猜想圆周长与圆的要素(直径或半径)的关系,借助Hawgent皓骏动态数学技术,展示圆半径变化的数据和圆周长的变化,助力学生发现圆的周长与直径的比值的关系,最后讲出圆周率发现的历史故事,在点拨“变中不变”数学思想的同时渗透数学文化。本环节设计具有授人以“鱼”的同时授人以“渔”和“欲”的作用,在破解教学难点、促进学生积累数学基本活动经验和体悟数学基本思想方法的同时,潜移默化地渗透了数学文化,提升了教学有效性。
参考文献:
[1]梁万里.重视几何直观 培养核心素养:以“圓的周长”教学片段为例[J].小学教学参考,2019(6):24-25.
[2]邱贻根.教不越位 学要到位:“圆的周长”教学设计与评析[J].教学月刊:小学版(数学),2009(4):33-35.
[3]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[4]唐剑岚,陈圆.基于“鱼渔欲”三位一体优化教学理念的数学创课设计:以“一次函数的图象与性质”的教学为例[J].中小学课堂教学研究,2017(12):34-37.
