构建数学模型 渗透模型思想

张婷婷

数学模型的构建在学生数学学习的过程中起着十分重要的作用，它不仅能为学生的数学表达和数学交流提供有效的途径，而且也为学生在数学学习和现实问题的解决之间搭建了重要的桥梁。借助数学建模，能够使抽象的数学知识变得直观，学生能准确地理解所学数学知识的内在意义。在小学数学课堂教学中，作为教师，应该充分认识到数学建模的重要作用，加强数学建模思想的渗透，要从不同角度去引导学生在头脑中建立数学模型，让学生经历数学模型的构建过程，感受数学模型的重要作用。同时，教师还应该不斷地设计一些具体的情境，让学生借助构建数学模型，去分析实际问题、解决实际问题。

一、在情境中感知数学模型

构建数学模型的前提是充分感知数学模型所关注的对象。因此，在教学中，我们应该让学生通过充分的感知，找到众多事物中具有共同特性的一类事物，通过分类、分层的一步步了解，抽象出这类事物的共同特征和内在的联系，在这个过程中使学生能够积累丰富的表象经验。基于此，教学中，我们应该充分重视情境的创设，要通过创设有效的情境，为学生的充分感知提供必须的感性材料，要使学生通过全方位的感知，从情境中逐渐体会、感知所学数学知识的本质特征或数学知识之间的相互关系，为学生的准确建模提供基础。

在教学人教版《义务教育教科书·数学》三年级上册“分数的初步认识”一节课时，为了让学生能够在头脑中建立起分数的数学模型，我创设了“分苹果”的情境，使学生对分数的思想进行了充分的感知，为学生的后续建模打下了扎实的基础。课前，我通过与学校食堂沟通，预先让食堂师傅充分准备了一些苹果和果盘，并让学生自己准备了安全的塑料水果刀。

上课时，我为学生准备了实物的教学情境。要求学生在小组合作中实物感知并讨论：将四个苹果平均分成两份，每份是多少个？这样做的目的，一方面是为了让学生能够回忆起除法的意义，另一方面，也为“分”的理解作了铺垫。然后，我要求学生在小组合作中实物感知并讨论：两个苹果平均分成两份，每份是多少个？目的是能让学生列出除法算式，并在头脑中建立“平均分”的概念。接着，我要求学生在小组合作中实物感知并讨论：一个苹果平均分成两份，每份是多少个？这样，学生就会感受到一个苹果再按照原来的方法就“不够分”了，该怎么办呢？这样就自然而然地引出了分数的概念。最后，我要求学生在小组合作中实物感知并讨论：一个苹果平均分成2份，每份是多少？平均分成3份、4份呢？这样，学生一方面在切苹果的实物操作中兴趣盎然地感受到了什么是平均分;另一方面，通过一层层的分类感知，他们也在头脑中逐渐清晰了“平均分成几份的份数就是分数当中的分母，取其中的一份或几份就是分数的当中的分子”。这样，他们就初步建立起了分数的数学模型。以此类推，学生对于其它分数的描述，也就能结合实际情况表达分数的意义了。

二、在探究中建构数学模型

《义务教育数学课程标准（2011年版）》指出：“动手实践、自主探索与合作交流是学生学习数学的重要方式。”因此，教学中，教师要给足学生动手操作的时间和空间，通过让学生去自主探索、合作交流，去经历知识的产生过程。只有这样，学生才能在探索的过程中和对学习材料的使用中发现问题，进而才能主动归纳和提升，最后建构出能让所有人都能理解并认可的数学模型。

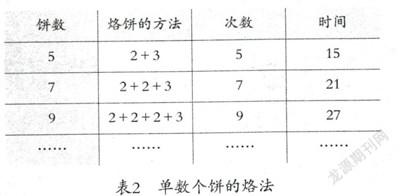
如在教学人教版《义务教育教科书·数学》四年级上册的“烙饼问题”时，我们可以让学生自主去探索，并逐步构建出数学模型。首先，可以让学生去自主探索“烙2张饼至少需要多少时间？”在烙2张饼的自主探索过程中，学生在辨析中很容易地就能明白：“2张同时烙需要6分钟”。这样，他们就能能够初步体验到烙饼中的优化思想。其次，“如何尽快烙好3张饼？”是这节课的关键点和难点。因此，在自主探究烙3张饼的最优化烙法时，可以让学生借助学具来进行动手操作和直观演示。同时，可以使用交互式电子白板来演示两种烙法的对比，让学生发现：充分利用锅内的空间，使得每次锅里同时烙两张饼，这样最节省时间。学生在直观中思考，在自主探究中发现，从而感悟到了什么是运筹思想。然后，可以引导学生小组讨论，并总结双数张饼、单数张饼的最优烙法。通过自住探究和小组讨论，学生得出了以下结论。（如表1和表2）

最后，可以组织学生观察得到的数据并寻找规律，在寻找规律中提炼出最优的烙饼法：总时间=饼数×烙一面饼的时间。这样，不仅能让学生领悟到数学方法的精巧和数学思考的美妙，而且还能让学生在具体的问题情境中进行自主探究，体验了数学模型构建的全过程。

三、在应用中拓展数学模型

建立数学模型还有一项重要的作用，那就是通过模型的建构来解决生活实际中的问题。让数学知识回归到生活中，是《义务教育数学课程标准（2011年版）》所倡导的重要理念。因此，在教学中，我们要能让学生体会到数学模型的实际应用价值，进而培养学生应用数学的意识和综合应用数学知识解决问题的能力，让学生体验模型的实际应用所带来的快乐。

如在教学人教版《义务教育教科书·数学》二年级上册“乘法的初步认识”时，通过设计情境图和学生的自主探究之后，学生已经在头脑中初步建立起了关于乘法意义的数学模型。这时，在练习的环节，教师就可以出示本班级的座位图，通过观察座位图，请学生算出本班一共有多少位学生。基于对乘法意义的已有建模，学生会列出乘法算式，即每组都是5人，6个组就是6个5，列式为：6×5或5×6。这样，学生根据乘法的意义，就构建起了解决问题的乘法模型。而在解决这样身边实际问题的过程中，学生也就会对乘法的模型更加明晰，而且也会了解乘法的实际使用价值。学生会发现，学习数学确实能够解决实际生活中所遇到的问题，在以后的数学学习中，学生就会有意识地去建模，并体会到用建模去解决生活中遇到的问题的快乐。

（责任编辑：杨强）