练在适当处，学向深度行

王广木

数学是一门用来表达事物空间形式与数量关系的科学，是人类思维的体操。在数学教学中，课堂练习具有重要作用，它可以帮助学生及时巩固知识、发展智力。教师要重视课堂练习内容和形式的设计，更要重视练习出示的时机，在学生学习的关键处，为学生设计一定的练习活动，让学生及时内化知识，发展能力。笔者结合教学实践，谈谈如何适时地在教学中进行课堂练习，提高学生学习实效。

一、练在生长处，搭建支架

作为教师，要充分分析学情，了解学生已有的知识经验，弄清新知学习所需的知识基础，在学生知识生长处为学生安排课堂练习，帮助学生在旧知基础的土壤上，主动地建构新的知识体系。如，在人教版四年级上册“除数是整十数的笔算除法”的教学中，笔者简单导入后，就为学生设计了如下课堂练习。

第一题：口算估算。

60÷30=2 480÷60=8

62÷30≈2 484÷60≈8

第二题：列竖式计算。

除数是两位数的笔算除法的计算原理与除数是一位数的笔算除法相同，只是试商的难度加大了。因此，笔者在学生已有知识基础上设计了除数是整十数的口算、估算，为学生试商做好充分的准备，设计除数是一位数的笔算除法，让学生回顾笔算的方法，如商的位置、余数必须比除数小等知识，为学生学习新知搭建支架。学生在教师搭建的支架上学习新知，促进学生主动地、有深度地进行数学学习。

二、练在薄弱处，夯实基础

教师要立足学生知识的薄弱处，为学生设计有针对性的课堂练习，帮助学生夯实基础，发展技能，积累数学活动经验，发展数学能力。如，在教学人教版小学数学四年级下册“乘法分配律”时，笔者设计了以下课堂练习。

第一题：说一说。请你用自己的话，同桌互相说一说乘法分配律。

第二题：比一比。8×（125+7）和8×（125×7）的计算结果一样吗，为什么？请你算一算。

第三题：选一选。下面三个算式，正确的是（ ）。

A. 56×（19+28）=56×19+28

B. 32×（7×3）=32×7+32×3

C. 64×64+36×64=（64+36）×64

第四题：练一练。

99×14+14 101×99 25×44

小学四年级学生的观察、比较、概括、归纳能力有限，学习了乘法分配律后，容易受到乘法结合律的负迁移，常常混淆乘法分配律和结合律，在运用上错误百出。于是，笔者设计了说一说、比一比、选一选、练一练四个练习活动。“说一说”是为了帮助学生识记乘法分配律;“比一比”是为了加强乘法分配律和乘法结合律的对比，避免学生混淆;“选一选”是为了深化学生对乘法分配律的理解;“练一练”是为了帮助学生灵活运用乘法分配律。这一系列的课堂练习，针对学生学习的薄弱处展开设计，有效地帮助学生巩固知识、发展能力。

三、练在易错处，弥补缺漏

教师为学生设计的课堂练习，要立足学生知识运用的易错处，将学生带进教师设置的学习“陷阱”，让学生在练习中主动发现错误，思考错误产生的原因，探寻避免错误的方法，为进入更深层次的学习打好基础，提高思维的缜密性和深刻性。如，在人教版小学数学四年级上册“因数中间或末尾有零的笔算乘法”的教学过程中，笔者在学生易错处设计了如下的课堂练习，帮助学生熟练掌握简便笔算。

第一题：写出下面的乘法算式的末尾各有几个零。

340×70的积末尾有（ ）个零，340×50的积的末尾有（ ）个零;

125×8的积的末尾有（ ）个零，250×40的积的末尾有（ ）个零。

第二题：判断下面的题目有错吗，有错的话请改正。

第三题：笔算。

440×60 360×25 580×12

学生在三年级已经学习了因数中间有零的计算，因此学生学习重点就是掌握因数末尾有零的简便笔算方法。由于学生受到“笔算时相同数位对齐”的思维定式的影响，多数学生在计算时出错较多，有的学生没有用简便笔算，有的学生忘记在积的末尾添零，有的学生在不该出现零的地方出现了零。为了帮助学生掌握因数末尾有零的简便笔算方法，笔者设计了以上一组课堂练习。第一题，帮助学生理解影响积末尾的零个数的因素;第二题，巩固因数末尾有零的简便笔算;第三题，运用因数末尾有零的简便笔算进行计算，加深对计算方法的理解和掌握。这样的课堂练习，在学生易错的地方适时强化，有利于帮助学生扫清知识障碍，及时弥补缺漏，推进学生的数学学习。

四、练在提升处，强化能力

学生学习了教材知识，经历了一定的观察、操作等数学活动，具备了一般的数学能力。然而，学生有主动发展的需求，仅让学生具备一般数学能力是不能满足学生发展需求的，教师还要重视提升学生的数学能力。此时，课堂练习便可以发挥很大效用。教师通过课堂练习为学生提供了具有挑战性的学习任务，让学生在具体情境中尝试解决问题，通过发散思维、集中思维等探寻解决问题的方法，在不断尝试中形成新的能力。如，在人教版小学数学五年级下册“旋转”的教学过程中，在学生认识旋转三要素，理解图形旋转前后大小和形状不变，位置改变，理解了图形旋转的本质特征后，如何深化学生对“旋转”的认识，培养学生思维的灵活性，提升学生能力？笔者设计了如下题目。

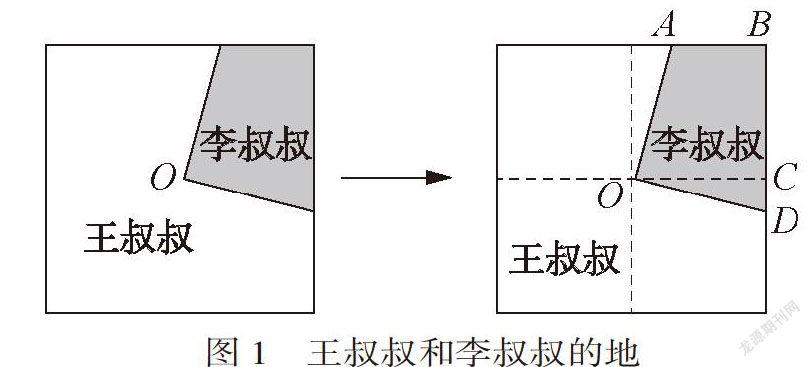
王叔叔和李叔叔共同种一块正方形菜地（如下图），O是正方形的中心，这两块地形状都不规则，种起来很麻烦，两人商量重新分这块地，你知道李叔叔应分得这块地的几分之几吗？

这样的题目，密切联系实际，富有童趣。学生在解决问题过程中，經历观察、想象、操作、描述等一系列活动，数学能力得到发展提升。在解决问题过程中，学生发现，要知道李叔叔应该分得这块地的几分之几，需要通过添加辅助线的方法，将李叔叔的土地进行分割，将不规则的图形转化成规则的图形，再利用旋转的知识进行解决。因此，可以将分割后的直角三角形COD绕点O逆时针旋转90°（或者绕点O顺时针旋转270°）;或者将直角梯形AOCB绕点O顺时针旋转90°（或者绕点O逆时针旋转270°）。在解决问题的过程中，让学生通过观察、想象等一系列数学活动，经历正向思维和逆向思维的交互，运用“转化”的数学思想方法，培养了学生的数学表达能力，提升了学生空间想象能力和问题解决能力。因此，教师要在学生能力提升处，适时设计一定的课堂练习。

本文系福建省教育科学“十三五”规划2018年度一般课题“基于大数据的个性化校本作业实践研究”（课题编号：FJJKXB18—397）系列成果之一。