一题多解在矩形翻折模型问题教学中的应用

王海虹

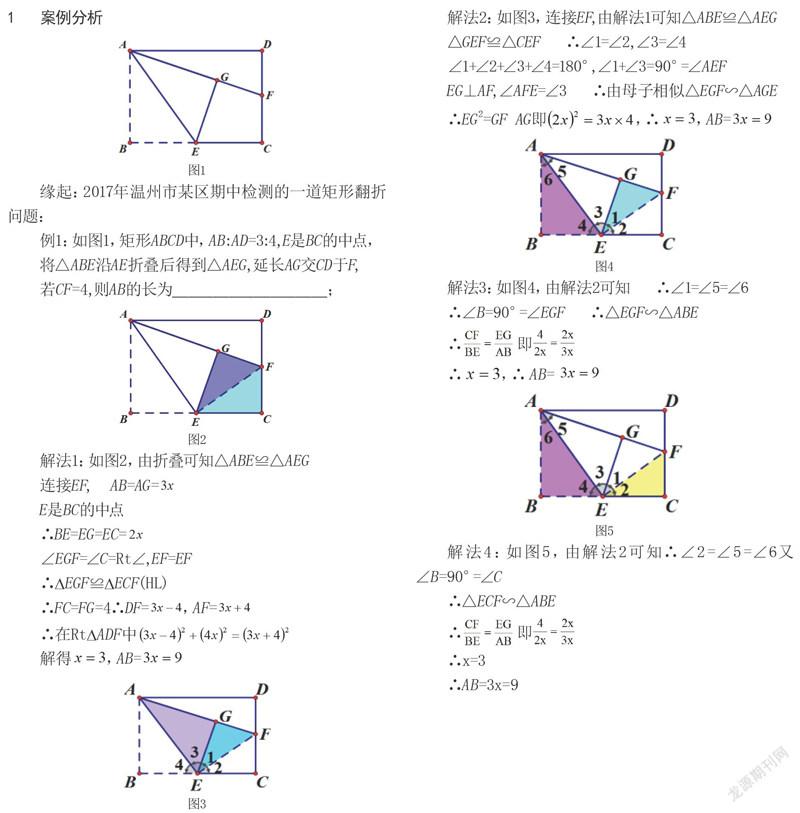
【摘 要】数学离不开解题，如何让学生通过精解题目，做到深刻理解概念、扎实掌握基本知识，提高思维水平，从而在面对变化多端的题目时，游刃有余，使难题迎刃而解。本文通过“一题多解，多解归一，多题归一，同模通法”等方式进行案例分析，解决这一疑问。

【关键词】模型;一题多解;同模通法

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2019）34-0058-02

2   反思

解法分析：在矩形翻折问题中出现的常见模型是全等三角形：△ABE≌△AEG，及新构造的△EFG≌△EFC，从而把问题转化为Rt△ADF中三边，通过勾股定理得到一元一次方程模型来解决线段长的问题;若出现K型三等角模型可利用三角形相似或者等角的同名三角函数，转化为比例式求解线段长。

3   结语

通过矩形翻折的例子，发现解决矩形翻折类问题的核心是研究翻折前后的变化，尤其要抓住过程中的不变量——全等图形;其次抓住条件中的K型三等角条件可以构造全等三角形，或者用相似三角形来求相应的边角;面积法、勾股定理也是常用的方法。抓住一类问题，通过一题多解、同模通法的方式，拓宽学生思路更是有效的教学手段[1-3]。

【参考文献】

[1]李兴军.一题多解解决矩形翻折模型问题[J].思维与数学教学理论，2017（31）.

[2]沈哲.一题多解与多题一解的数学探究策略[J].新教育时代，2016（7）.

[3]王飞.一题多解在数学矩形翻折模型問题中的探索策略[J].数学教学杂志，2017（5）.