直觉思维在“极限”教学中的应用

叶建华

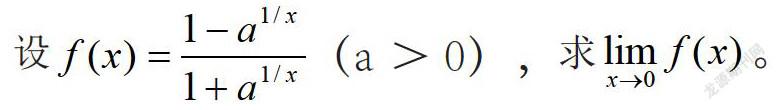
【摘 要】直觉思维在科学认识过程中发挥着重要作用，特别在理解高等数学众多抽象理论中有着不可小觑的作用。该文将对直觉思维在无穷极限教学实践中的应用进行探讨。

【关键词】直觉;高等数学;无穷极限

【中图分类号】G642  【文献标识码】A  【文章编号】1671-8437（2019）34-0001-02

直觉，是极具活力和创造性的思维因子。有人把爱因斯坦的用脑模式简述为：经验—直觉—概念和假设—逻辑推理—理论，在这个经典模式里，直觉是不可或缺的重要环节。因此。在高等数学教学过程中，保护学生的直觉思维、培养学生直觉思维运用能是其重要的。

1   直觉思维的特征

直觉是一种客观存在，它既是一种思维形式，也是一种认知过程。直觉思维是指在经验的基础上，迅速摆脱固定逻辑规则的约束而直接领悟事物本质的一种思维形式。它是指不受固定逻辑规则约束，未显示出完整的推理过程，而是由前提直到结论的迅速识别过程。因此，直觉具有直接性、快速性、综合性、模糊性等特征。

2   直觉思维在“极限”教学中的应用案例

2.1  应用直觉思维理解无穷极限

2.1.1  无穷极限的几何直觉

《庄子》记载：“一尺之锤，日取其半，万事不竭”。数学家刘徽在割圆术中提出“割之弥细，所失弥少，割之又割以至于不可割，则与圆合体而无所失矣”，这可视为中国古代极限观念的佳作[1]。这类经典例子可以让学生从几何角度直观认识到极限的问题主要是无限问题，它能使学生通过对某些有限问题的考察，直觉地得出关于无限的结论。

2.1.2  逼近概念的语言直觉

逼近概念可以用“你想有多近，事实上就比你想象的还要近”来表达，与此类似的“无穷小”“无穷大”的概念，也用类似的语言去表达，使学生快速形成关于“无穷”的直觉认识，进而逐步形成逼近概念。

2.2  應用直觉思维培养极限估算能力

数学中的估算其实就是一种典型的直觉思维，即是运用各种运算技巧、摒弃干扰因素、抓住问题主干进行的快速近似计算策略。

这里在的条件下， 是主干，那么去掉干扰因素，原式可以等价于而在的条件下，，所以常数1才是其主干，于是，“估算”不仅是快速的近似计算方法，其实质是一种直觉思维方式，它要求突出主干、忽略枝节、回避干扰、直奔主题。

3   直觉思维局限性的应对

在教学中教师应使学生注意到直觉不足的一面：直觉不一定正确，具有或然性;直觉不够精细，大多属于模糊性直觉，需要经过严密的论证;直觉易受经验的影响，所以存在固有模式的限制。估算，既然是近似计算策略，必然有误差或错误。因此，教学中严谨的反思过程也是必不可少的。

为什么会错？其实是因为的主干是差，是一个比更高阶的无穷小。只有把这个主干表达出来，才可以得到正确的答案。

最后借用前苏联物理学家福克的一句话来说明直觉的重要性，“伟大的、以及不仅是伟大的发现，都不是按逻辑的法则发现的，而都是由猜测得来;换言之，大都是凭创造性的直觉得来的。”因此，我们应该将直觉思维充分应用到教学中，培养和提升学生的直觉思维能力[2]。

【参考文献】

[1]左路.化工类线性代数本质与几何直觉培养教学例证研究[J].数学学习与研究：教研版，2019（1）.

[2]赵后银.基于直觉思维培养的高中数学教学实践探索[J].数学教学通讯，2018（36）.