考虑支座材料劣化的斜拉桥地震易损性分析

冯 环,武芳文

(1.滁州职业技术学院，安徽滁州239000；2.长安大学公路学院，陕西西安710064)

桥梁作为交通的枢纽和抗震救灾的生命线，一旦发生震害将带来难以估量的损失，而桥梁抗震性能是桥梁研究中的重要领域。在地震发生时，橡胶支座拉伸扯断率、水平剪切刚度等力学性能的退化会导致其对桥梁结构减隔震效果产生不利影响。所以，研究橡胶支座在恶劣环境与自身老化共同作用下出现的基本力学性能变化非常必要。

铁道部科研院于1994—1995年将在铁路上分别服役16年、19年和22年的板式橡胶支座分解并进行相关力学性能测试，结果显示，其剪压弹性模量增大约20%，表面橡胶的老化厚度达5 mm，并推算支座的使用期限能达到80～110年[1]。裴若娟等[2]讨论了对叠层橡胶支座耐久性起主要作用的外界因素，并对支座进行加速老化试验，结果表明，540天加速老化试验后，支座徐变量为支座厚度的6%，支座刚度增大20%左右。BROWN[3]对多种橡胶材料进行自然老化和热老化研究结果表明，橡胶材料经40年自然老化，其拉伸强度会减小35%左右；伸长率也会同时下降将近48%左右。KIM[4]讨论了钢筋混凝土构件加固前后的地震易损性，CHOI[5]研究了美国中部与东南部桥型的地震易损性。BASOZ[6]用Northridge地震所采集的大量震害信息，通过回归分析法拟合出经验易损性曲线。

综上所述，国内外针对橡胶支座的相关性能研究已经取得较大的进展，大多数研究结果表明，随着橡胶支座服役年限的增长，支座的水平和竖向刚度也会出现增长，这与支座老化后其硬度增大有关。同时，支座橡胶伸长率与扯断率则出现减小的情况。但是，对橡胶支座材料在恶劣环境下性能退化的研究还较少，同时，桥梁支座在地震灾害中的表现，对结构的抗震性能起着至关重要的作用[7]。本文在考虑支座材料劣化的情况下，探讨支座性能的退化对桥梁抗震性能产生的影响，从而可以更好地指导实际工程中的抗震设计与地震风险评估，有效减轻桥梁结构自身损害。

1 理论模型支座材料劣化的规律

处于海洋环境中的支座材料的性能退化较为明显，本文对海洋环境中的橡胶支座材料劣化加以分析。海洋是一个非常复杂的系统，其环境因素具有恶劣、复杂、多变的特点。目前认为海洋区域可以分为6个区域，具体情况如表1所示。

表1 不同海洋区域的侵蚀特点

大部分海洋区域都具有较强的侵蚀性，这对直接暴露于海洋环境中的桥梁橡胶支座是相当不利的。在桥梁结构中，多数情况下都会采用橡胶支座，其支座性能的退化主要表现在橡胶材料的老化和螺栓、连接板与封板等钢构件锈蚀。支座对桥梁所提供的变形适应性以及产生的消能减震作用主要依靠橡胶材料，钢构件的作用是保证支座和桥梁结构之间的有效连接，除非出现特别强烈的地震使其撕裂或分离。因此，对于钢构件的锈蚀对支座性能产生的影响，本文在建立计算模型时将不予考虑，而只考虑支座自身性能变化。

橡胶支座在经历老化和海蚀作用下其力学性能会发生较大的变化，而力学性能的变化将会直接导致橡胶支座在地震作用下的性能出现变化。随服役时间的增长，橡胶材料的老化和腐蚀主要表现为剪切刚度的退化，本文根据已有的试验研究数据拟合出如下橡胶支座随服役时间增长的刚度变化公式：

K=0.989 3+0.003 9T

(1)

其中，K是水平剪切刚度值变化系数，T是支座使用时间(a)。

从以上公式可以得到服役年限分别达到60 a和120 a时本文所选用橡胶支座的水平剪切刚度变化值，如表2所示。

表2支座剪切刚度变化值

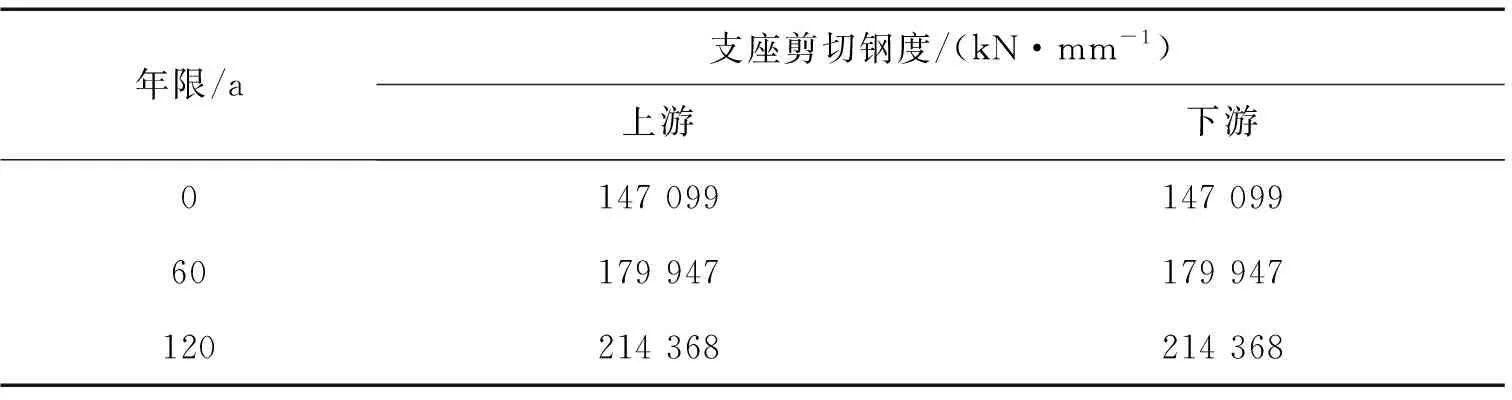
年限/a 支座剪切钢度/(kN·mm-1)上游 下游0147 099147 09960179 947179 947120214 368214 368

2 考虑支座材料劣化的易损性分析方法

本文参考普通连续梁桥分析的思路，先对桥梁主要部位进行损伤标记，再确定适用于斜拉桥的易损性分析法。通过对橡胶支座在环境影响下的性能退化研究成果进行归纳总结，将所得到的结论应用到所建立的斜拉桥动力计算模型中，重新生成“地震动-结构”样本，利用增量动力时程分析法对所建立的桥梁模型进行分析，获得其在不同地震激励下主要构件不同损伤状态的超越概率，得到全寿命期内的易损性曲线。

2.1 考虑支座材料劣化的易损性分析的具体流程

在实际过程中，支座性能的退化会导致其对桥梁结构减隔震效果产生不利影响。桥梁结构在考虑支座材料劣变影响下的易损性分析流程图如图1所示。

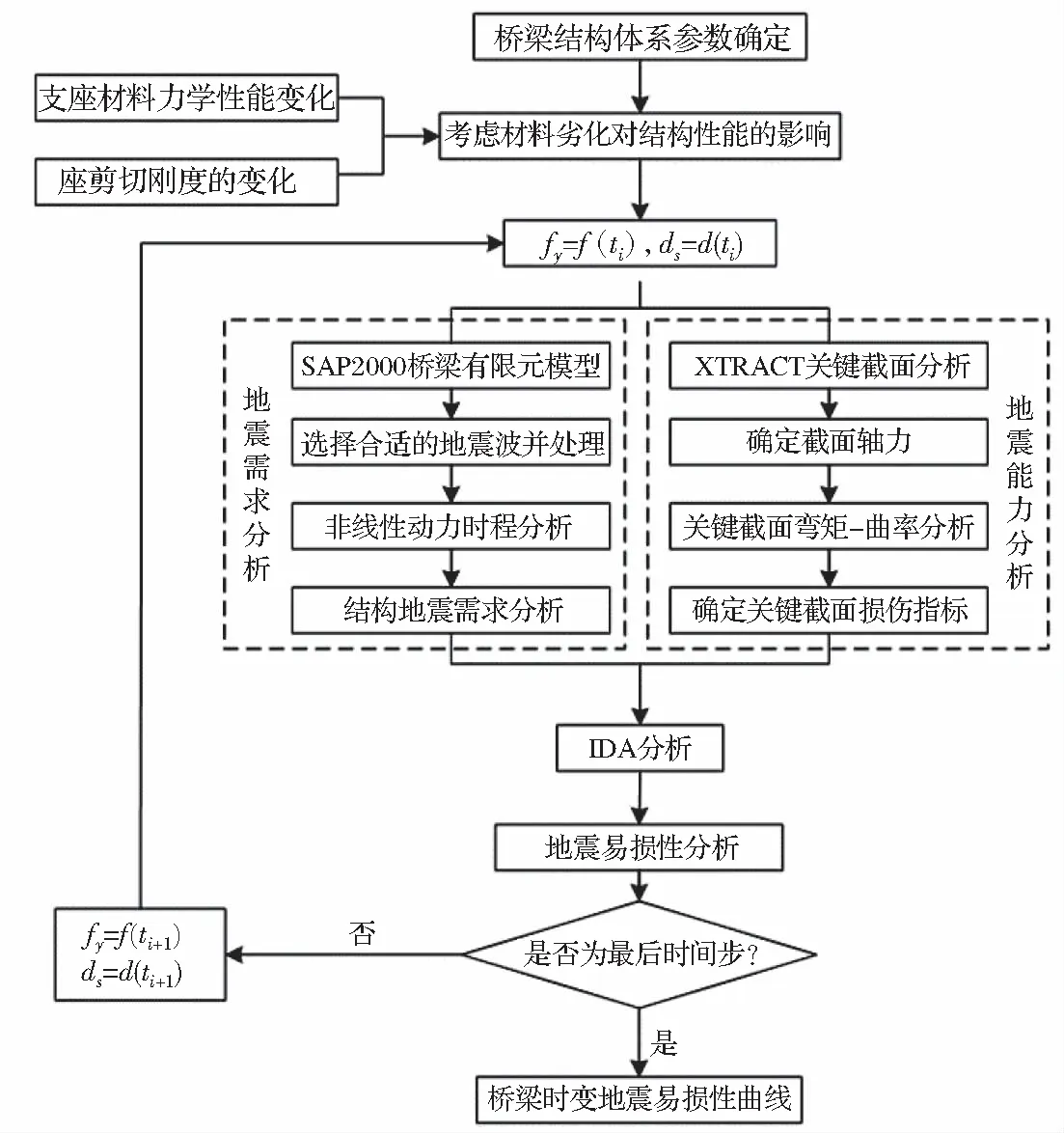
图1 易损性曲线建立流程

2.2 增量动力分析理论

增量动力分析(incremental dynamic analysis，IDA)是为地震动设置一系列倍数当作外荷载输入进行分析，目前已成为获得抗震需要谱与能力谱的重要分析法。在使用IDA之前要设置好倍数步长、损伤目标与强度目标。IDA即将单一时程分析变为增量时程分析，对各条IDA曲线都进行多次时程分析，又分为单地震动和多地震动记录IDA法。IDA法以结构动力弹塑性分析为基础，其基本原理是通过合理的调幅系数对地震动记录进行调幅，使所选取的地震动强度指标IM(一般为PGA、值速度PGV、Sa等)逐级增大，用调幅后的地震波对同一结构体系进行多次时程分析，获得结构在不同地震强度等级下的最大响应DM(顶点最大位移、最大基底剪力、层间位移角、关键截面曲率等)，最后通过动力非线性时程分析得到的一系列地震动强度指标IM与地震反应参数DM数据，绘制出反映IM-DM关系的IDA曲线，利用IDA曲线可以得到易损性曲线，用来评估结构的抗震性能。其基本分析步骤如下：

(1)根据设计图纸，建立所分析结构的有限元模型；

(2)根据结构以及场地特性，选取合理的地震动强度参数和地震反应参数；

(3)选择满足分析要求的多条地震动记录(一般选取10～20条就能满足分析精度要求)，经试算确定合理调幅等级和调幅系数，对选定的地震波进行调幅。为了计算方便，一般采用等步长进行调幅；

(4)在有限元模型中，分别输入调幅后的地震波进行时程分析，并根据分析数据绘制出各截面的IDA曲线；

(5)根据相同方法分别输入其余地震波对结构进行激励，将同一截面的多条IDA曲线绘制在同一坐标系内，并对其进行统计分析用以评估结构的抗震能力。

2.3 基于IDA法的时变易损性曲线建立流程

为了得到更加直观的结果，在分析中通常假定结构体系抗震能力和地震需求服从对数正态分布。易损性函数如公式(2)所示。

(2)

其中，SD为结构地震需求中值；SC为结构抗震能力均值；βD|IM为在给定强度指标时地震需求D所对应的条件对数标准差；βC为抗震能力C的对数标准差。

本文基于桥梁结构IDA非线性时程分析进行易损性曲线的绘制，通过对结构有限元模型进行多次弹塑性时程分析所得到的地震响应数据，采用能力需求比(Capacity/Demand Ratio)对数非线性回归分析形成桥梁结构的易损性曲线。

其计算方法可由公式(3)～(5)表示：

μ(t)=α(t)[ln(Sa)]2+b(t)[ln(Sa)]+c(t)

(3)

(4)

(5)

其中，a(t)、b(t)、c(t)为结构服役至时间t时的回归估计参数；Sa为反应谱加速度；Sr(t)为结构服役至t时间点的回归曲线残差平方和；μ(t)为结构服役至t时间点的能力需求比对数均值；σ(t)为结构服役至t时间点的能力需求比方差。

3 考虑支座劣化的斜拉桥地震易损性分析

3.1 有限元模型建立

本文以某双塔双索面斜拉桥为例来进行主塔的地震易损性分析。该桥主桥采用双塔双索面半漂浮体系，设计使用年限120 a，主跨400 m，采用钢混叠合梁，边跨设计为混凝土梁，主跨和边跨的连接为边跨混凝土梁部分伸入主跨。由于桥梁沿纵向采用半漂浮体系，该体系具有频率小、周期大的特征，在地震发生时可以较为有效地消耗地震产生的能量。而该桥主塔对主梁在横桥向进行限位，辅助墩、过渡墩和主梁在横向固结，因此主塔和主梁的连接部分，辅助墩、过渡墩和主梁连接部位将更容易遭到地震的影响而发生破坏。

3.1.1 桥面系的模拟

模型中，桥面系的模拟采用单梁模型，该方法把主梁的质量、惯性矩、抗弯刚度和扭转刚度集中在中间的单梁单元。同时将主梁和拉索之间用刚性连接相连，即所谓的“鱼骨式”。该方法不能将主梁抗扭转的作用考虑在内，然而主梁的刚度和质量体系的模拟是较为准确的。本文重点对塔柱进行分析，所以在建模过程中采用单主梁模型。

3.1.2 拉索的模拟

利用等效模量法，主要通过对弹性模量进行反复的修正以达到降低拉索非线性影响的作用。采用索单元进行模拟，随着单元拉力的变化，修正的弹模随之发生变化。修正弹性模量可由公式(6)求得。

(6)

其中，E为斜拉索的材料弹性模量；G为拉索总体重量；σ为拉索水平方向倾角；H为索力在水平方向的分力；Eg为高强钢丝的弹性模量；Ag为高强钢丝的总面积。

3.1.3 支座的模拟

图2 桥梁的动力分析模型示意图

有限元模型中的边界条件要和结构实际的边界条件相对应。桩基础的模拟采用弹簧单元，考虑土对桩的侧向和竖向约束，桩身隔一段间距布置两个方向的仅受压弹簧支承。支座的模拟按照给定的支座刚度条件进行输入。通过有限元软件SAP2000建立桥梁的动力分析模型(图2)。

3.2 主塔截面易损性曲线建立

通过对桥梁结构进行各条地震波作用下的非线性时程分析，提取桥塔与墩柱关键截面地震时曲率的需求值。再通过能力需求比的方法对相应的曲线进行拟合，获得这些曲线的相关重要参数，之后将不同等级地震动下桥梁各关键截面损伤概率的离散点用B样条曲线相连得到各个关键截面的易损性曲线。下面以所建斜拉桥下塔底截面轻微损伤易损性曲线的建立加以说明。

计算得到这一截面在不同等级地震动发生时的曲率需求值Sd，再把Sd和该截面轻微损伤曲率指标Sc1作比值，并对获得的比值取对数，再对相对应的Sa值取对数，将这两个值绘制在直角坐标系中，其中前者为纵坐标，后者为横坐标，见图3。

图3 下塔底的曲率需求与轻微损伤指标拟合曲线

把图中各个分散的点通过二次多项式的方式进行拟合，假定Sd与Sc1都服从正态分布，所以Sd/Sc1取对数后也服从正态分布。利用多项式回归将ln(Sd/Sc1)的均值μ转化为ln(Sa)的二次多项式见式(7)。ln(Sd/Sc1)的标准差σ，即回归曲线的拟合标准差如式(8)。

μ=a[ln(Sa)]2+bln(Sa)+c

(7)

(8)

其中，Sr为n个样本的残差平方和。

因为ln(Sd/Sc1)服从正态分布，并且通过各个不一样的Sa值能够获得相应的期望与拟合标准差，所以由式(9)能够得到下塔底截面在不同等级地震动时的轻微损伤超越概率，其实质是累积正态分布函数值。

(9)

地震波数量越多，将会得到越精确的分析结果，由于本文所选用的地震波数目有限，所以对于统计分析所得的结果通过B样条曲线的方式进行拟合。通过公式(7)与公式(8)获得不同等级振动对应的期望值μ与标准差σ，再代入公式(9)得到关键截面的超越损伤概率。

把下塔底截面在各个地震动等级时的损伤概率离散点绘制在直角坐标系，并通过B样条曲线把这些点连接起来得到截面易损性曲线，对其他三个损伤状态采用相同的方法进行分析和曲线拟合。对其他关键截面进行非线性时程分析，提取数据并进行曲线的拟合，获得其余各个关键截面的易损性曲线。

3.3 考虑支座劣化的横向地震易损性对比分析

当周期T2=1.689 s时。横桥向质量贡献率达到最大值，所以将T2时刻对应的谱加速度当作地震动的强度指标，这样可以减小横桥向地震需求的离散性。进行易损性分析之前，对横桥向反应谱加速度进行重新调整(表3),g为重力加速度。

表3 各强度等级的反应谱加速度

根据支座剪切刚度的变化情况，对横桥向各个易损截面进行地震易损性分析。图4～图7给出了横向各易损截面随支座年限增长产生的易损概率变化曲线。

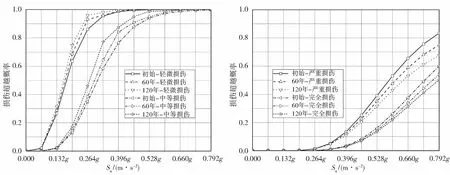
(a)未考虑支座性能变化 (b)考虑支座性能变化

图4支座性能变化前后下塔底截面易损性对比

(a)未考虑支座性能变化 (b)考虑支座性能变化

图5支座性能变化前后下塔顶截面易损性对比

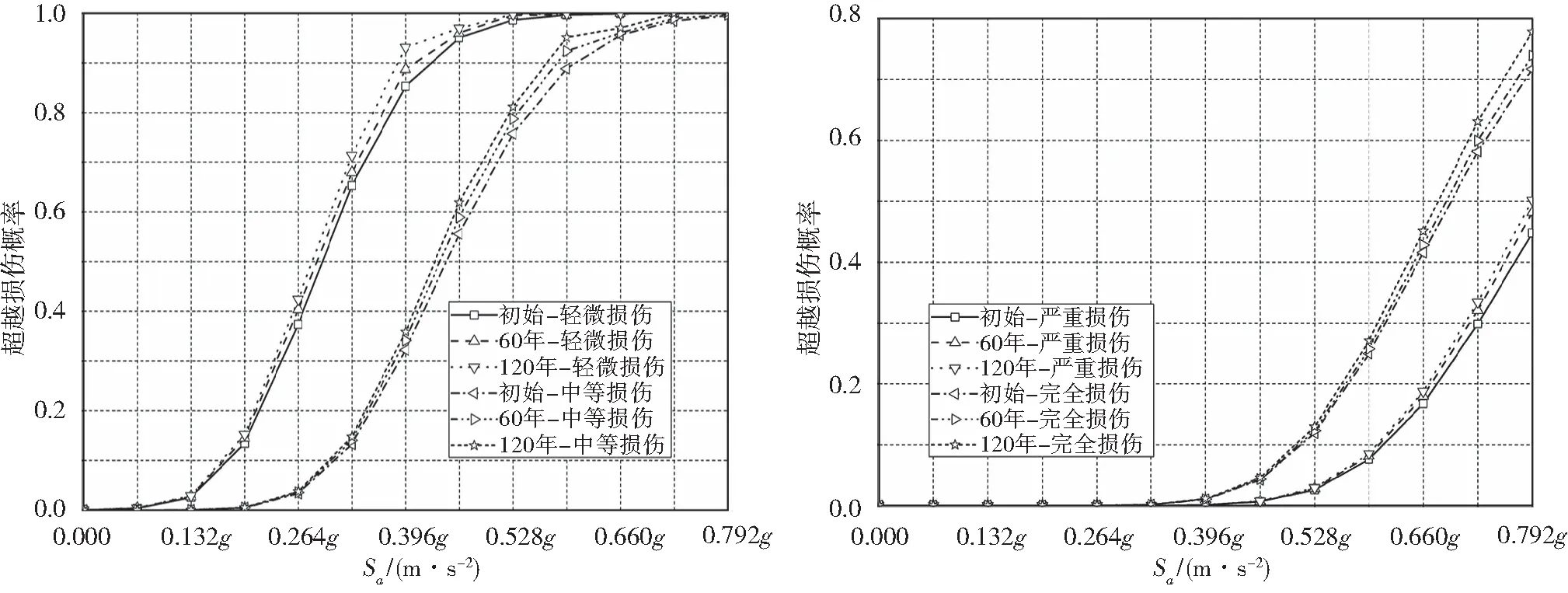
(a)未考虑支座性能变化 (b)考虑支座性能变化

图6支座性能变化前后上塔底截面易损性对比

(a)未考虑支座性能变化 (b)考虑支座性能变化

图7支座性能变化前后上塔顶截面易损性对比

对以上对比图进行分析可知：横向地震作用下，支座性能变化对关键截面易损性产生的影响也较为显著，易损截面的位移依然没有发生变化，各个截面出现各种不同等级损伤的概率呈现了较为相似的变化。以下塔底截面为例，支座性能的变化对轻微损伤和中等损伤的影响主要集中在中等强度地震动时，两者损伤概率增大的最大程度分别达到了10%和19%。对严重损伤和完全损伤的影响主要在中高等级地震动，与纵向地震发生时相似，两者的损伤概率呈现略微降低的趋势。

4 结论

通过比较分析各构件的地震易损性曲线，得出斜拉桥的下塔底部截面和上塔底部截面受地震作用时的易损截面。横向地震作用时，在考虑了支座材料性能的退化后，对桥梁结构进行全寿命周期的截面易损性对比分析，结果表明，随着服役时间的逐渐增长，桥梁在地震时容易损伤的截面不会出现变化，但是桥梁各个关键截面在地震作用下出现损伤的概率会发生相应的变化，即服役年限的增长使截面出现轻微损伤和中等损伤的概率增大，但发生严重损伤和完全损伤的概率减小。支座的变化对桥梁结构的地震响应产生了较为明显的影响，是桥梁全寿命期内影响桥梁抗震性能的重要因素。