基于小波变换与LabVIEW的时栅信号采集分析系统设计

赵勇图，彭东林，郑 永，王 伟，王露露

(1.重庆理工大学机械工程学院，重庆 400054；2.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆 400054；3.重庆理工大学时栅传感及先进检测技术重庆市重点实验室，重庆 400054)

0 引言

时栅位移传感器是一种新型角位移测量传感器，其通过对一路参考信号和一路含角度信息的行波信号进行比相，用高频时钟脉冲对相位差做插补，对插补脉冲数计数、累加后，通过相对坐标转换公式计算出空间位移，完成空间测量[1]。杨继森等设计了基于STM32F4芯片的时栅位移传感器信号处理系统，将驱动电源、信号采样以及数据处理与误差补偿集成在一片芯片中，实现了系统的集成化[2-3]。但其数据采样率受到单片机的性能限制，无法完成大规模数据采样，不利于时栅测量稳定化。目前的时栅信号处理系统主要有驱动电源、信号采样、数据处理与误差补偿模块，由FPGA和DSP硬件组合来完成[4-6]。时栅传感器的信号处理系统模块化设计的不足：各模块使用各自的处理器芯片使生产成本高、程序复杂；不同种类芯片需要不同的供电源，不仅使电源模块设计复杂，而且还带来了不必要的干扰信号；单片机对大规模数据处理能力有限，导致传感器精度下降。

为此，本文采用数字信号处理方法，设计了一套基于LabVIEW软件开发平台的时栅位移传感器信号采集分析系统，实现了集信号采集，数据分析与处理，结果显示与保存功能于一体，解决了编程周期长、复杂程度高的问题，并提高了系统信号处理能力。

1 磁场式时栅位移传感器原理

磁场式时栅位移传感器按照激励类型不同可分为两相形式和三相形式[7]。本文使用三相式，图1为其原理图，图中V为旋转磁场的转速；v为转子转速。在定子上绕空间互差120°的a、b、c三相激励绕组，利用特定的精密正交激励电源，向a、b、c相施加频率相同、幅值相同、相位互差120°的交流励磁电压，分别为：

ua=Umaxcos(ωt)

(1)

ub=Umaxcos(ωt+120°)

(2)

uc=Umaxcos(ωt-120°)

(3)

式中：ua、ub、uc为三相电压，V；Umax为幅值，V；ω为激励频率，Hz；t为时间，s。

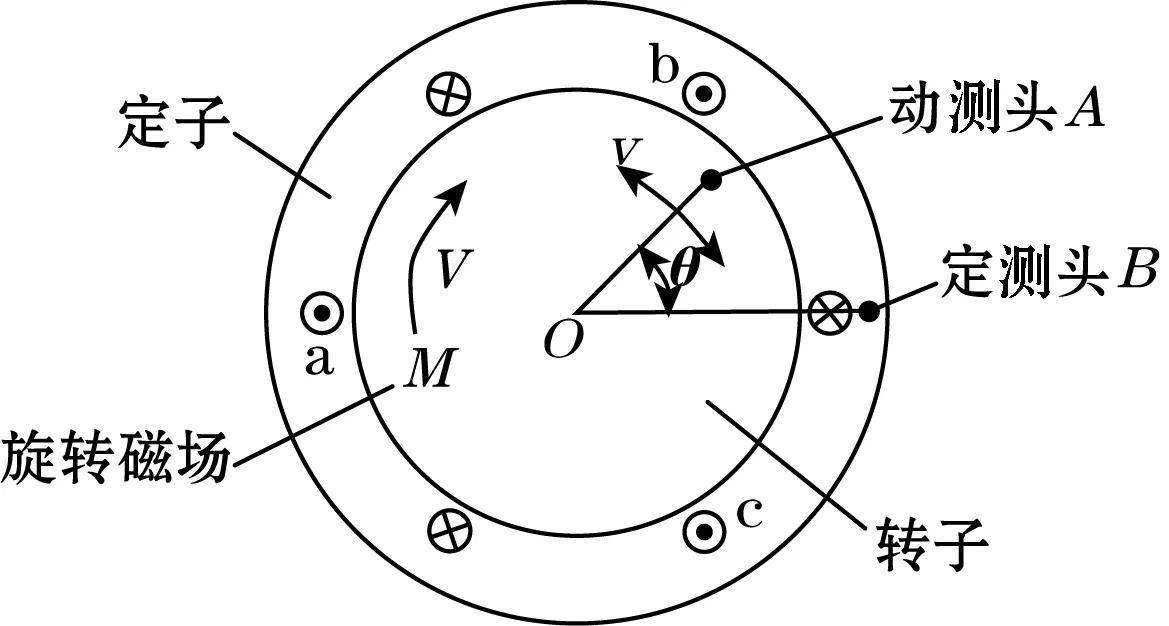
图1 磁场式时栅原理图

三相激励电压通过定子和转子之间相对结构产生气隙磁导，磁导作用在转子上感应出驻波电势：

ea=KUmaxωcosθcos(ωt)

(4)

eb=KUmaxωcos(θ+120°)cos(ωt+120°)

(5)

ec=KUmaxωcos(θ-120°)cos(ωt-120°)

(6)

式中：ea、eb、ec为驻波电势，V；K为比例系数。

将式(4)～式(6)叠加，得到行波磁势e：

(7)

式中：Umax为激励电压幅值；θ为转动角度。

将此信号与激励电源的参考电信号同时输入时栅信号处理电路，通过高频时钟插补技术和数字比相技术获得反映转子角位移的时间差，图2(a)为传统时栅信号处理方法流程图。图2(b)为本系统时栅信号流程图。

系统摒弃了FPGA+DSP处理模块，将调理后的信号直接通过PXI-5922采集卡采集，之后用小波变换做降噪处理，最后用数字比相法计算测角值。

(a)传统时栅信号处理流程图

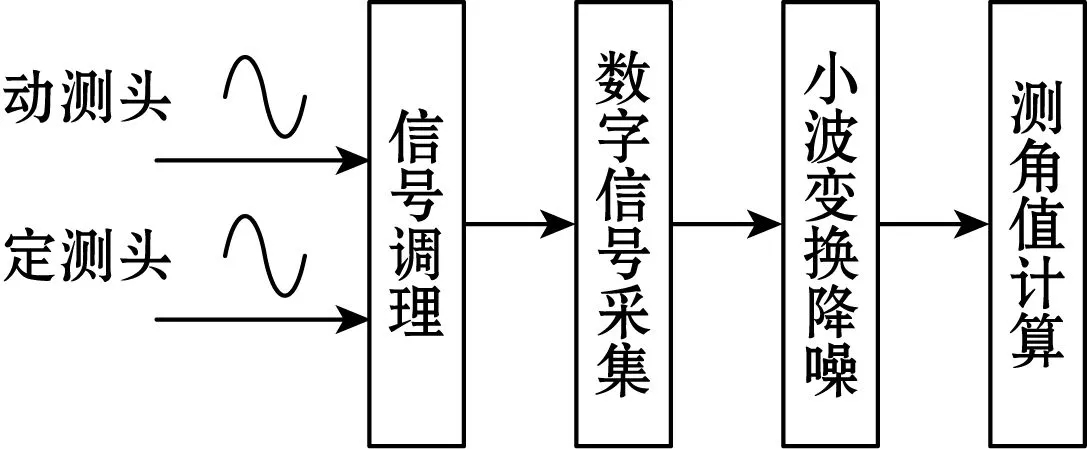
(b)本系统时栅信号处理流程图图2 时栅信号处理流程对比

2 系统的硬件设计

时栅信号处理系统包括数据产生、数据采集和数据处理3个模块。系统由FPGA特定模块产生激励电压，通过气隙磁导在转子上感应出磁势，经信号调制后接入PXI-5922采集卡，采样后传输至PC机中。为了保证行波信号的一致性，利用硬件触发采样，从FPGA主芯片中引出一脚，产生与参考信号频率相同的方波信号作为触发信号，并在采集卡中设置外部触发采样模式，当系统检测到方波的上升沿时，系统开始采样，这样可以得到连续稳定的行波数据。最后，用PC分析处理数据。图3为整个系统的硬件图。系统采用PXI-5922高性能数字采集卡，其具有24位8通道同步数据采集功能，采样率最高可达15 MS/s，支持模拟和数字采样及采样数据自校准功能。在100 kS/s的采样率下，其电压噪声仅为1.2 μV，采样过程稳定，结果精度高，并有LabVIEW配套软件，具有采样率高，数据传输量大，可视化程度高等特点。

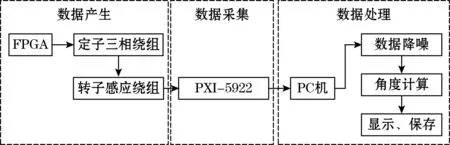
图3 时栅信号处理硬件系统图

3 系统的软件设计

图4为磁场式时栅位移传感器信号处理系统的工作流程图。首先检测激励信号是否产生，若检测到三相电压信号，则将其送入时栅传感器，电流经过定子线圈，通过三相绕组结构，在转子上感应出行波磁势，其次检测外部触发源信号，当接收到上升沿信号时，触发系统采样，PXI-5922采集卡将行波数据采集至PC机，此时的信号由于受环境条件和硬件电路的电气误差等影响，含有一定的噪声，为了获取精确的测角值，用小波变换对原始信号进行降噪处理，最后用数字比相计算方法，对去除噪声后的信号进行测角值计算，作为最终的测角值。

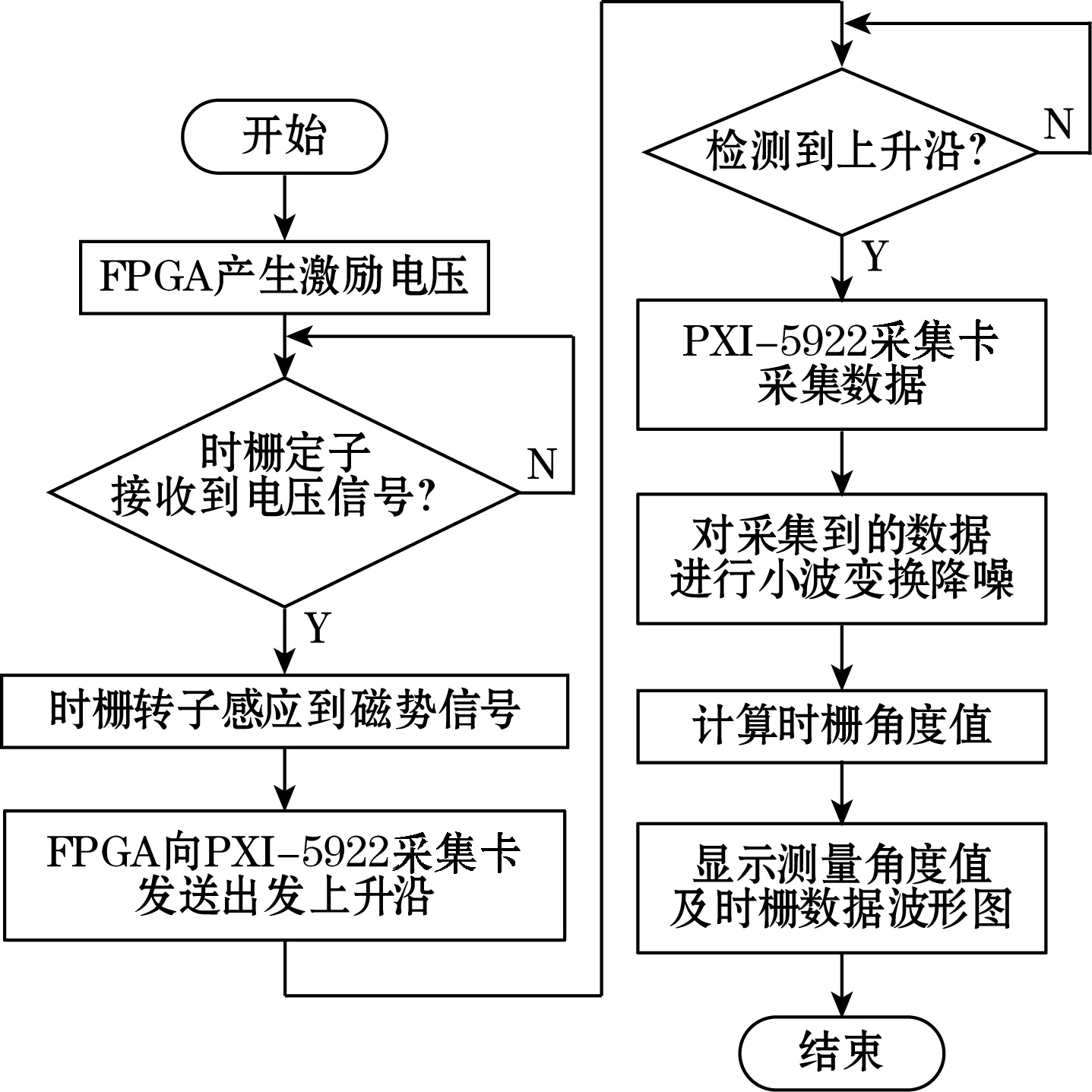
图4 系统工作流程图

系统中FPGA产生信号，PXI-5922采集卡采集信号，PC机处理信号。与传统编程采取的文本语言相比，LabVIEW使用G语言编程，界面更加友好直观，是一种直觉式图形程序语言[8-10]。本系统软件部分基于LabVIEW平台开发，包括数据采集，数据分析，数据显示与保存等子模块。

3.1 数据采集模块

本文采用硬件触发采样方法采集时栅数据，将

FPGA产生的一路方波信号通入PXI-5922采集卡，当PXI-5922采集卡检测到方波信号的上升沿时，开始采集数据，这样可以保证每次采样的起点相同，都处于过零点处，提高了时栅相位信号的稳定性。

本模块由LabVIEW中的数据采集子VI模块组成，其中niScope Initialize，主要完成采集卡的选择、初始化及内存分配等设置。niScope Configure Vertical可设置采样通道和电信号的幅值。niScope Configure Horizontal Timing可设置采样率、采样点数、采样通道个数等。niScope Configure Trigger(poly)为采样系统设置触发源、触发模式、触发电压、触发延时等参数。niScope Initiate Acquistion的功能为对指定通道的数据进行数字化采样，并以数组的形式存储至PC机内存中，等待下一步读取操作。niScope Fetch(poly)将内存中的数据读取，并将信号参数归类至不同的数据中，以便下一步做数据显示和处理。图5为数据采集模块的流程图。

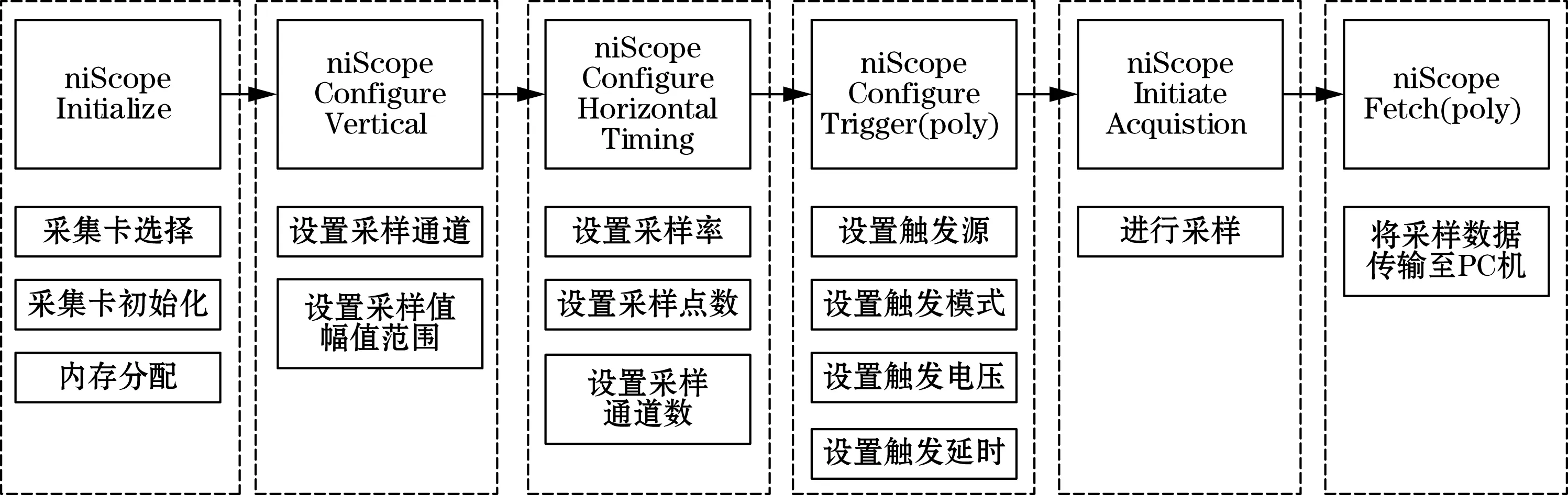
图5 数据采集流程图

3.2 数据处理模块

由于采集到的时栅行波信号受传感器电气误差、实验环境等因素影响，精确度仍达不到要求，需对数据进行进一步处理。本模块结合LabVIEW和MATLAB软件平台，使用MathScript节点功能将数字信号处理算法集成至一个程序流程图中，可以方便快捷地嵌入算法至系统中，无需再添加硬件或额外编写代码至外部处理设备，体现了系统的集成化。

设采集到的原始时栅信号f(n)的表达式为

f(n)=g(n)+e(n)

(8)

式中：e(n)为噪声;g(n)为有用信号，对时栅信号进行小波降噪的目的是降低e(n)以恢复g(n)。

时栅行波信号的频率为400 Hz，属于低频频段，而噪声信号为高频信号，对信号中的高频噪声进行分离和去除，同时尽量保留低频信号不受影响。传统的时栅数字降噪方法是对采集信号进行傅里叶变换，然后在频域内做低通滤波或带阻滤波。但傅里叶变换的缺点是不具备时频分析的局域性，在降噪的同时信号的突变部分变得平滑，而小波变换可以保留信号中的高频成分[11-13]。图6为时栅信号的小波降噪流程图。

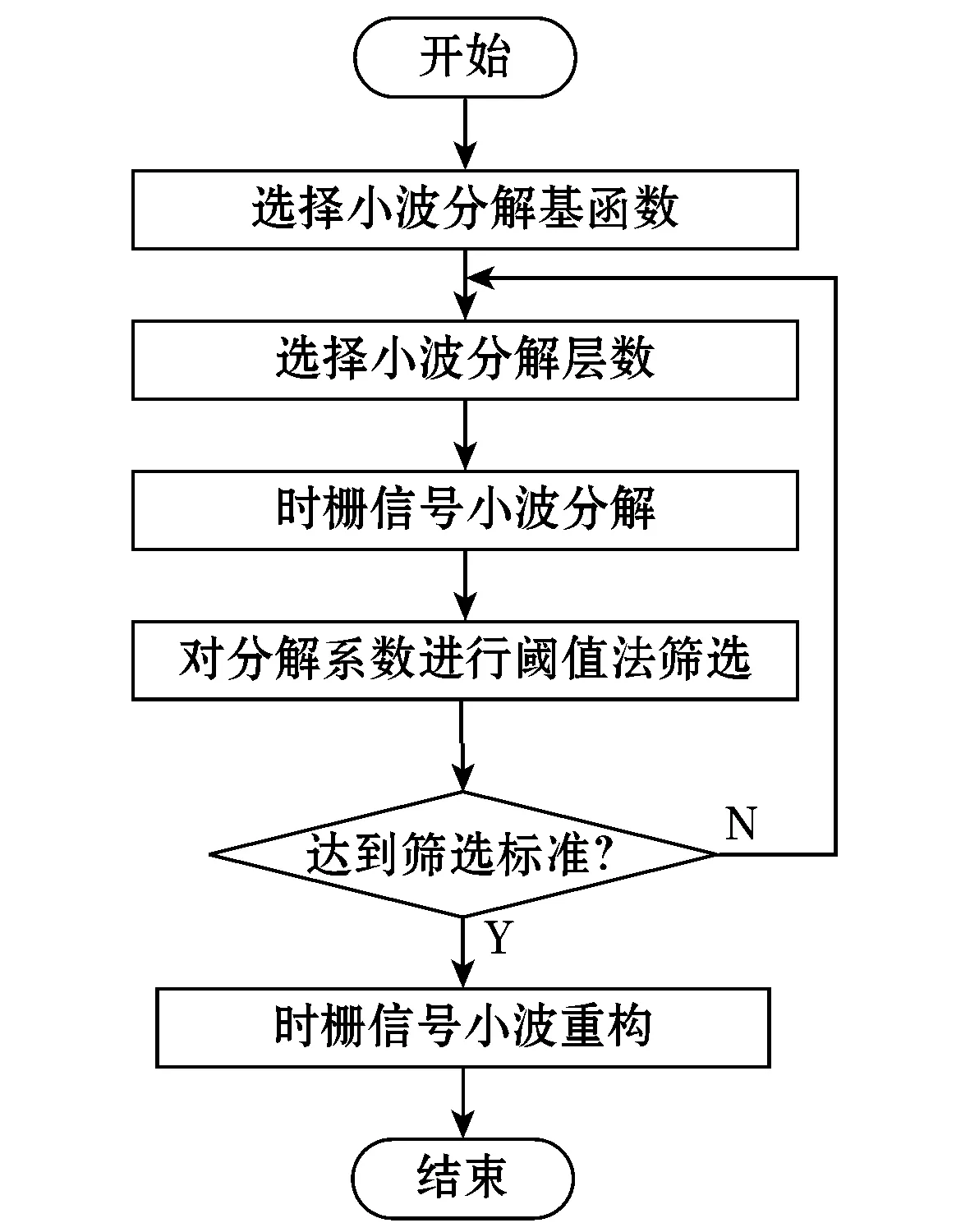
图6 时栅信号的小波降噪流程

时栅信号的小波降噪算法有4个步骤：

(1)选择小波分解的基函数，常用的小波函数有Haar小波、双正交小波、Morlet小波和db3小波等。由于db3小波函数适合正弦信号分解，其分解效果最佳，故本系统选择db3小波函数。

(2)选择小波分解的分解层数，分解层数的选取主要参考信号的信噪比和系统的响应时间，若信噪比越低，则理论上需要选择更高的小波分解层数，才能达到一定的去噪效果，但较高的分解层数又会影响系统的运作时间，在较高转速下，系统相应时间条件不满足高层小波分解的条件。综上，结合时栅信号的信噪比较高，同时又处于运动状态，需要保证一定的时效性，选择进行三层小波分解，在转速条件允许下，足以达到去噪效果。

(3)进行小波分解后，需要对分解的高频和低频系数进行阈值处理，阈值的选择方法有以下两种：

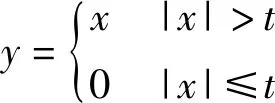
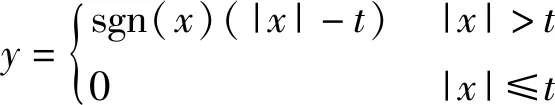
式中：y为阈值处理后的信号；x为原始采样信号；t为阈值。

硬阈值法类似于滤波器，设定一个值t，将原始采样信号中数据的绝对值与t比较，将绝对值小于等于t的数据全部设置为0，并保留大于t的数据，将比较后的数据作为阈值处理后的信号，这种方法较绝对，不适用于周期变化的正弦信号。时栅信号中大部分为有用信号，即g(n)>e(n)，而软阈值法将设定的阈值进行定向收缩，即按照某一固定量向零收缩这个系数，时栅信号的频率为400 Hz，可据此设定阈值，将信号向400 Hz周围频次收缩，将误差信号剔除。

(4)根据第3层的低频系数和从第1层到第3层的高频系数，对处理后的高频和低频信号进行重组，得到降噪后的时栅行波信号。

3.3 数据显示与保存模块

为了能更直观显示时栅传感器产生的行波信号，设计了数据显示模块，本模块将绘制时栅信号图形和保存时栅数据功能集成在一个绘图子VI中，由于PXI-5922采集卡采集到的时栅行波数据为数组形式，其包含多个参数，其中计算行波值需要的参数有，二进制数据、增益因子和偏移因子，需要先经过解捆绑操作，将采样时间和行波电压提取为单一向量，再通过自适应计算，设二进制数据为b，增益因子为g，偏移因子为o，行波电压值解算公式为

本章中分析的数据均为年度数据，为了消除数据量纲和异方差性，在实证中需要对部分数据取对数形式。对于数据选取过程中以百分比形式出现的变量(X2、X5、X6、X7、X8、X9)，不再取对数，其它变量均取对数后再放入模型。根据以上分析，建立以下线性回归模型：

V=b×g+o

(9)

式中V为行波电压值，V。

将解算出的结果输出至PC机显示器中，在程序前面板中设置面板工具，在不借助示波器等其他外接仪器的情况下，方便进行查看、放大、保存图形数据等操作。

4 实验测试

为测试所设计的时栅位移传感器信号处理系统，建立了图7所示的时栅位移传感器实验台，包含大理石实验基台，RON886圆光栅(精度为±1″)，72对极磁场式圆时栅，PXI-5922高速采集卡，信号调制模块及显示器。将直驱电机转轴和时栅位移传感器及光栅的转子部分连接，使时栅位移传感器和光栅传感器同步采集，用RON886圆光栅数据作为基准，通过控制电机以8 r/ min旋转，得到不同的角度值，系统实时采集时栅位移传感器信息，上传至PC机中显示保存。图8为HMI界面。

图7 时栅位移传感器实验台

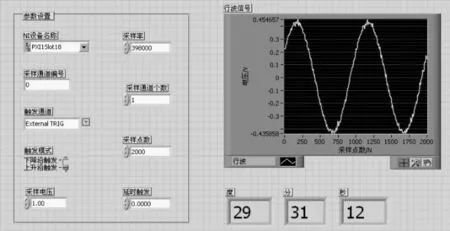
图8 时栅位移传感器信号的系统前面板

为验证小波降噪的效果，先对未经小波降噪的原始信号进行采集，图9为采集的数据。由图9可知，在未做小波变换前，信号的主要误差为随机型误差，产生此误差的主要原因为温度、湿度等环境变化导致的时栅激励信号不稳定，又由于行波信号幅值电压不到0.5 V，易受干扰，从而导致采样信号存在电气随机误差，这些误差将影响行波信号的零位位置，导致硬件电路的过零相位比较点不准确，从而影响最终时栅角度值。本系统使用的硬件电压比较器为LM211系列，其偏置电压在日常使用的环境下为0.7 mV，即信号的电压在0至0.7 mV以内，将不会触发比较，只有当信号电压值超过0.7 mV时，才判断为过零点，而原始信号由于存在噪声，在零位附近内多次超过过零阈值，这导致过零比较点的提前或延后，在进行相位比较计算时，将引入误差。

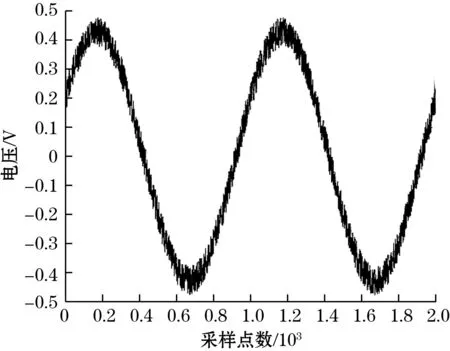
图9 原始信号

为此，对原始时栅信号进行小波降噪，选用db3小波基函数，三层小波分解层数，分解后得到的近似系数和细节系数见图10。由图10可知，三层近似信号中已去除大部分随机误差，可以得到较平滑的行波信号。随着层数的增加，细节系数的幅值逐渐减少，且频率逐渐递减，三层细节系数中其幅值范围已降至±0.05以内，证明原始信号中的误差已基本被滤除。

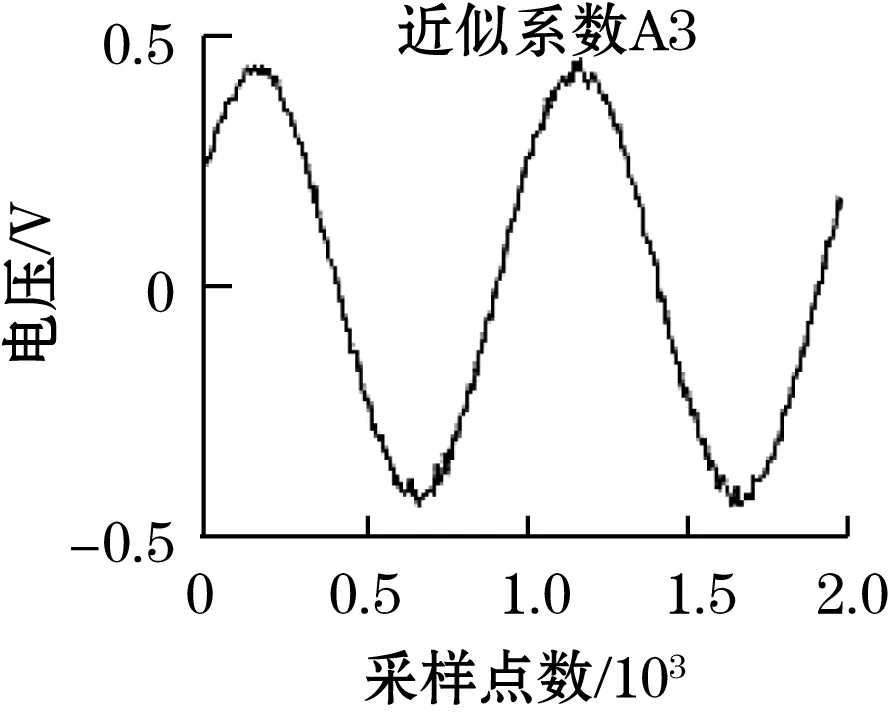
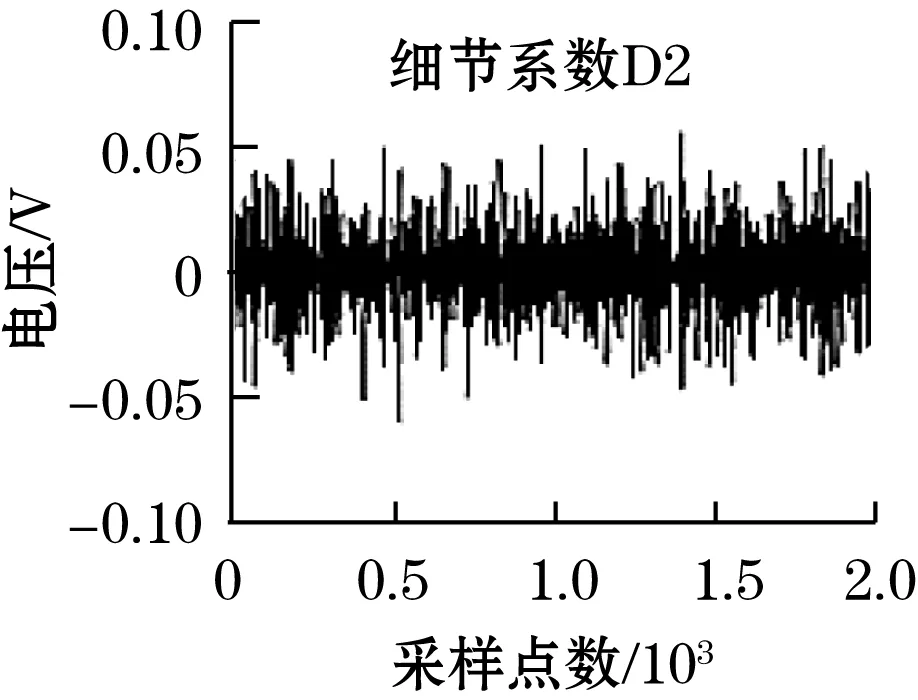
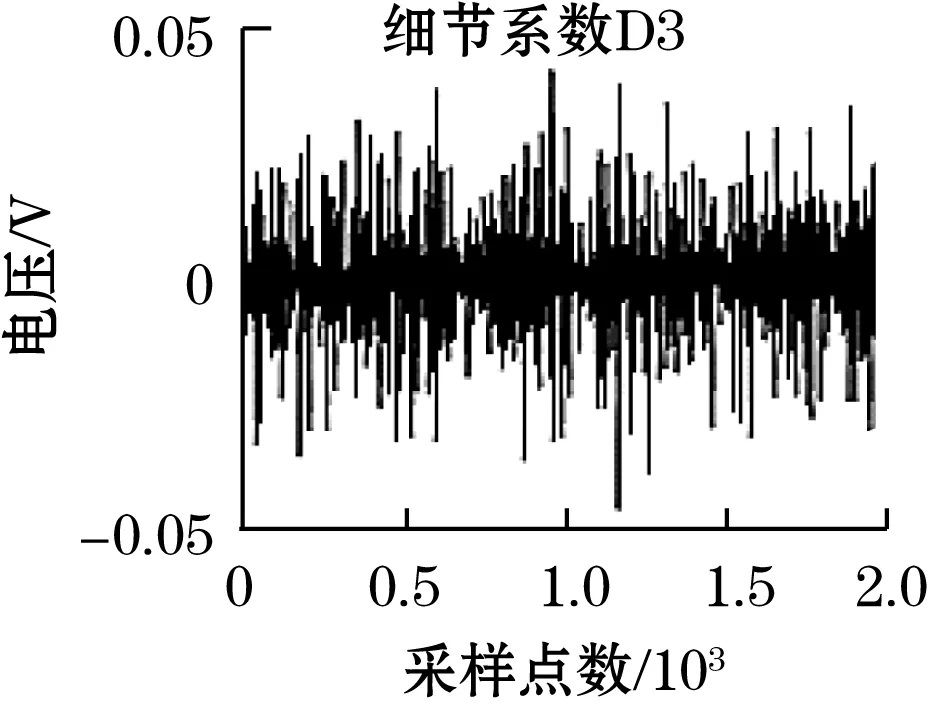
图10 小波分解得到的近似系数和细节系数

图11为降噪前和降噪后的信号对比，经过小波降噪后，信号质量有了明显的提升。

将图11中圆圈标注的位置，即原始信号和降噪后信号的同一过零位进行放大后，得到降噪前后过零位置的对比放大图(图12)，从图中可明显看出，小波降噪后的过零位已经不存在多次过零，即零点偏移的情况。

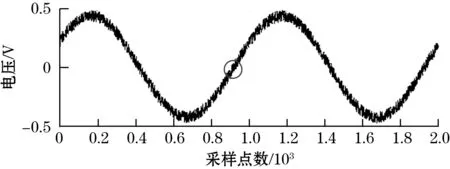
(a)原始信号

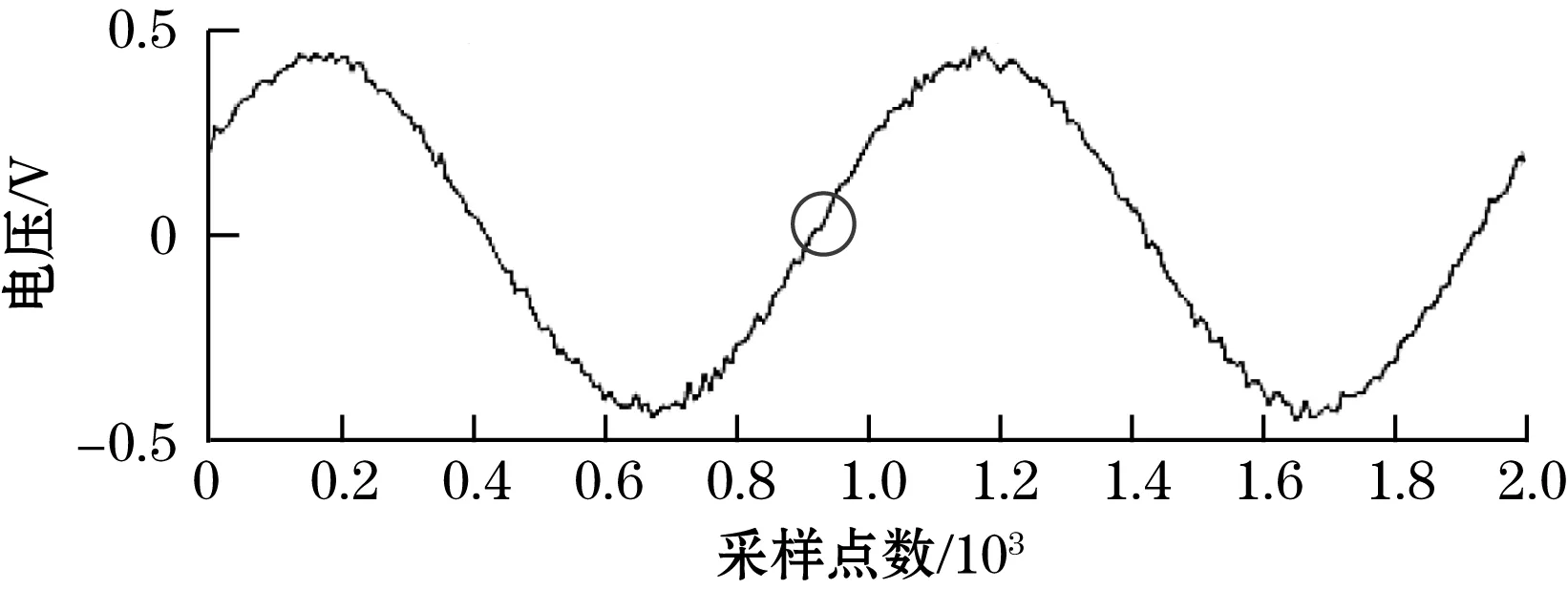
(b)降噪后信号图11 原始信号与降噪后信号对比

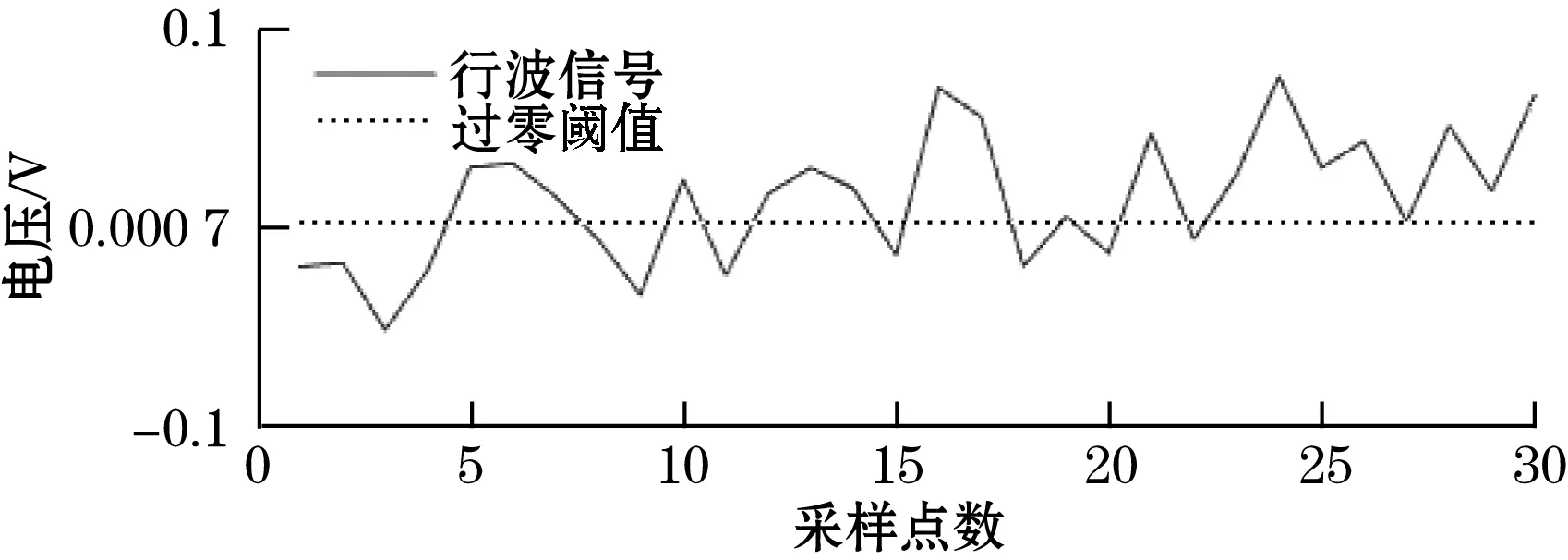
(a)小波降噪前行波过零位附近放大图

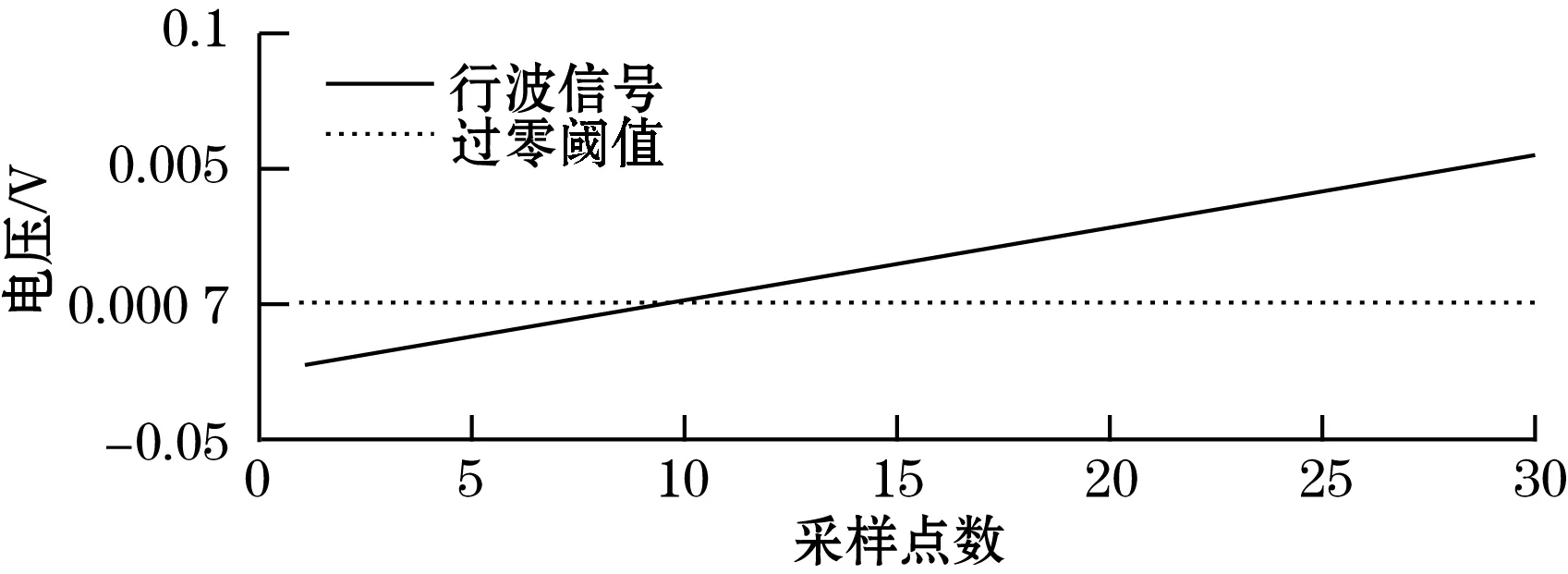
(b)小波降噪后行波过零位附近放大图图12 降噪前后行波过零点放大图

将降噪前后的过零点位附近的30个数据点进行提取，并将部分具有代表性的数据列为表1。由表1可知，降噪前在N=5、8、10、12处皆为过零点，而降噪后零位确认为唯一定点，即N=10处，按照角度误差计算公式(10)计算，可直接减少90″的相位误差。

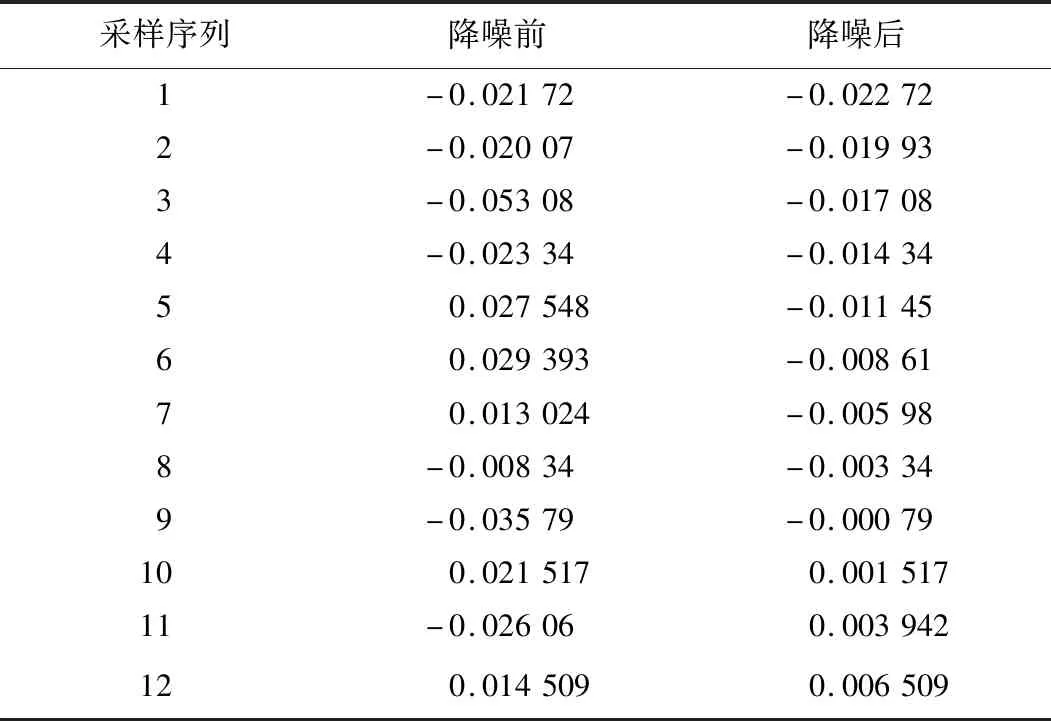
表1 小波降噪前后部分数据点对比表 V

(10)

式中：n为过零降噪前后首个过零点数差；N为一个周期的采样点数的总和。

最后，计算消除零点误差后的误差曲线，由磁场式时栅位移传感器误差特性可知，在每个对极内，检测值误差具有循环性。因此，只需对0°～5°范围内检测误差，即可获得传感器整周误差。在一个对极内随机检测100个点，以光栅值为基准，绘制时栅值的误差曲线，如图13所示。图13中，最大误差值和最小误差值分别为+1.62″和-1.81″，故磁场式时栅传感器的整周误差峰峰值为3.43″。

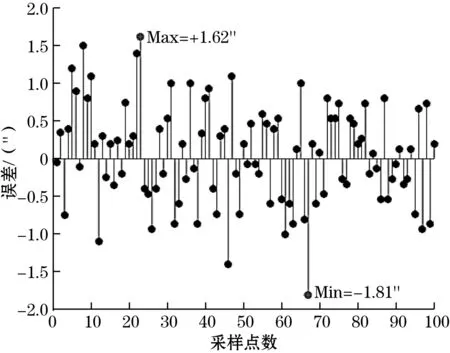
图13 小波降噪后的误差曲线图

5 结论

本文设计了一套基于LabVIEW的时栅传感器信号采集分析系统。系统具有数据处理能力强，通用性强，开发周期短等特点，结合数字信号处理方法，利用小波变换对时栅信号降噪，解决了由于零点偏移造成的时栅测角值偏差的问题，改进了传统方法中过零比较不稳定的缺点，使原始误差由90″降至3.43″。本系统可用于中低速时栅传感器信号处理，也可用于其他类似原理传感器测量系统，具有较强的数据处理能力和稳定性。