电动汽车充放电的优化管理

● 刘 洋

一、问题重述

（一）引言

为应对交通领域的石油资源消耗多、温室气体排放多的问题，世界各国政府都在积极推广电动汽车的发展。电动汽车的大规模发展离不开电力系统的支撑，但电动汽车无序充电行为随机性强、同时率高的特性给配电网带来负荷峰谷差增大、电压下降、损耗增加等挑战。同时，电动汽车作为移动式储能，在削峰填谷、提供电力系统辅助服务、协同消纳新能源等方面有广阔的应用前景。电动汽车与电网互动（Vehicle to Grid，V2G）作为一种对电动汽车充放电行为优化管理的方式应运而生。

（二） 问题提出

根据题目及提供的相关数据，解决如下问题：

第一，根据某城市100辆电动汽车一周的充电记录，分析电动汽车充电行为特征量的分布规律，为电动汽车充电行为建模，并计算规模化电动汽车的年用电量。

第二，根据一万辆车的充电电功率的分布以及问题一所得充电行为规律模型，计算24小时1万辆车的充电负荷曲线。并分析，在何种充电功率的分布下，既能满足用户需求，也能减少设备投资，并可降低电动汽车无序充电负荷的峰谷差。

第三，根据充电需求的记录和光伏发电功率的分布对充电站进行优化管理，在光伏全额利用和允许弃光的条件下计算24小时内充电站的最大利润。

第四，根据电网各个物理属性的限制以及根据不同时段用户充放电电价，使得电网有功网损最小值并且电动车车主总花费最小。

第五，综合以上各题对电动汽车、新能源充电站、电网互动之间的关系进行综合分析，对电动汽车与电网互动的综合规划进行分析预测。

二、问题分析

问题一：要求根据大量充电行为记录，建立充电行为模型，并求规模化电动汽车的年用电量。首先七天100辆车的样本数据进行预处理。因100辆车各天的充电行为没有必然的联系，所以将七天100辆车的样本数据简单合并为一天700辆车的样本数据。假设一辆车三种行为特征量（充电开始时刻、连接时长、充电电量）两两相互独立，互不影响，用MATLAB分别作出三个行为特征量的经验分布函数图像，并与泊松分布的分布函数图像对比。猜测它们均服从泊松分布，再利用K-S检验法验证猜测的正确性，并得到参数。分别写出三个行为特征量的分布律，再相乘即可得到电动汽车充电行为的规律。该模型可做时间和规模上的推广，最终只需根据充电电量的分布律，得到规模化电动汽车的年用电量。

问题二：要求计算24小时的充电负荷曲线，并计算不同充电功率等级的比例，使得用户需求得到满足，减少设备投资，并降低电动汽车充电负荷的峰谷差。首先，在本题中影响充电负荷曲线的因素有充电功率、充电开始时刻、连接时长，因此根据这三个因素的分布，采用蒙特卡洛模拟的方式，使用MATLAB软件绘制充电负荷曲线。进而求较优的不同充电功率等级的比例，这是一个目标规划问题，根据题意只需求出一个满足要求的比例即可。减少设备投资作为目标函数，即让投资最小；满足用户需求和降低峰谷差作为约束条件；最后检验是否满足题目条件。

问题三：要求计算在不同情况下24小时内最大利润。首先，对数据进行预处理，根据充电时刻计算在每15分钟内的需求量。得出结果后就能判断在此时间段之内是否需要购电或售电。将所有时间段内的利润进行加和，即得到24小时光伏全额利用可获得的利润。此问题为优化问题，以此利润做目标函数，是否需要购电或售电做约束条件，即可得到最大利润。对于允许弃光，就是可以将多余的光能弃用，只需在第一问目标函数中去掉向电网售电部分即可得到最大利润。

问题四：要求对配电网中电动汽车充放电行为优化。首先求电网有功网损最小值，采用动态规划的方法，对电网进行优化，进而采用分层序列法，将求得的电网有功网损的最小值作为约束，采用线性规划和蒙特卡洛仿真的方法，最终得到电动车车主总花费最小的充放电行为方案。

问题五：综合前四问的分析结果和方法，对电动汽车和电网之间信息的相互交流进行分析、综合评价，在深刻了解电动汽车发展意义的前提下，根据切实的问题结果和分析过程，综合评价未来电动汽车的发展。

三、基本假设

第一，EV用户在进行电能交换时无需等待；

第二，电动汽车各天的充电行为没有必然的联系；

第三，每一辆电动汽车的充电开始时刻、连接时长、充电电量三个行为特征量两两相互独立，互不影响；

第四，每一辆车在固定时间段内充电功率不变

第五，所有电桩都能正常进行充电

第六，电动汽车电池容量充满后立刻断电

四、符号说明

ζ1：充电开始时刻

ζ2：连接时长

ζ3：充电电量

t：（t-1）～ t时刻，i=1，2…

q：（q-1）～ q kWh，m=1，2...

h：（h-1）～h小时，j=1.2.3…

L：24小时充电负荷（kW）

N：车辆总数

Pr：第r级充电功率的平均功率，r=1,2,3

Q1：充电量之和

ai：第i个时间段内的售电电价

ti：第i个时间段内的光伏发电功率

Si：第i个时间段内的需求电量

li：第i个时间段内的购电电价

wi：0-1 变量

五、模型的建立与求解

（一）问题一的建模与解答

要求根据大量充电行为记录，建立充电行为模型，并求规模化电动汽车的年用电量。

第一，电动汽车充电行为模型的建立

首先将七天100辆车的样本数据进行预处理。因100辆车各天的充电行为没有必然的联系，所以将该样本数据简单合并为一天700辆车的样本数据，并将充电开始时刻的取值转化为数值型。这就相当于进行了700次试验，得到的结果记为样本X。

记充电开始时刻为ζ1、记连接时长为ζ2、记充电电量为ζ3，则（ζ1,ζ2,ζ3）是样本X上的一个3维随机变量。为了建立电动汽车充电行为的模型，则需要求出（ζ1,ζ2,ζ3）的联合分布列［1］。根据独立性假设，ζ1、ζ2、ζ3两两相互独立，则分别求出ζ1、ζ2、ζ3的边际分布，相乘后得到联合分布，进而求得充电行为模型。

对于充电开始时刻ζ1，设k为观察值，求得ζ1的经验分布函数其中k不大于样本X的样本容量n。根据Glivenko定理可知，用经验分布来近似理论分别是可行的。利用MATLAB的作图功能做出的经验分布函数的图像，如图1。

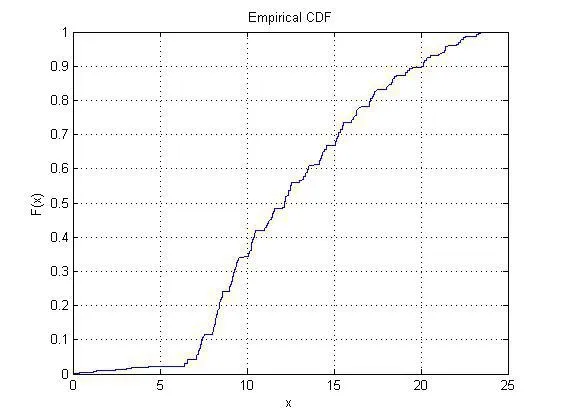
图 1 ζ1的经验分布函数图像

通过图1观测出ζ1的经验分布函数图像符合泊松分布函数分布图像的各种特点，推断ζ1服从泊松分布。进而利用SPSS软件对猜测进行检验，采用K-S检验法，检验出ζ1服从参数=12.73的泊松分布，检验结果如图4。其中ζ1的分布为

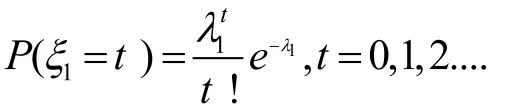
同理，分别对ζ2和ζ3进行以上操作，得出ζ2和ζ3的经验分布函数图像，如下图2和图3。

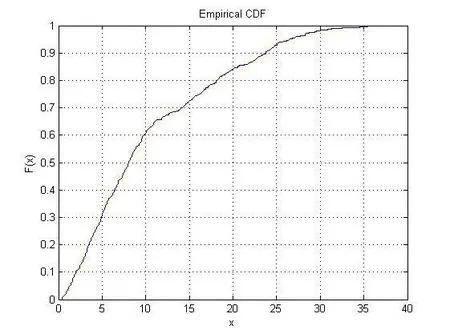
图 2 ζ2的经验分布函数图像

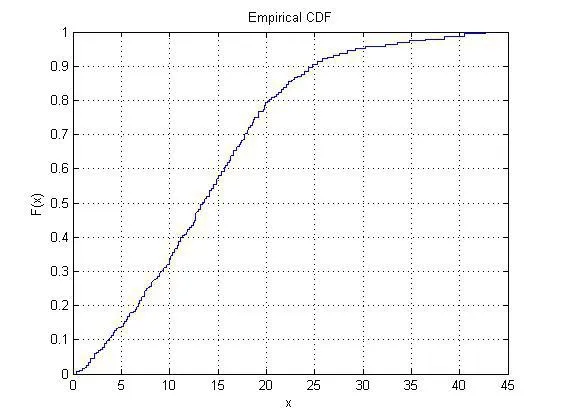
图 3 ζ3的经验分布函数图像

图 4 K-S检验结果图

得到ζ2和ζ3分别服从λ2=10.60和λ3=14.22的泊松分布，分布分别为

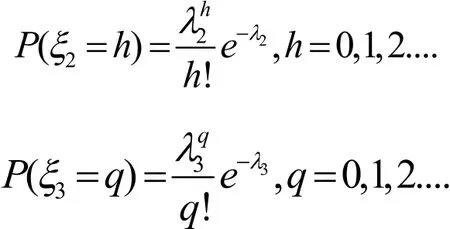
得到电动汽车充电的行为规律为

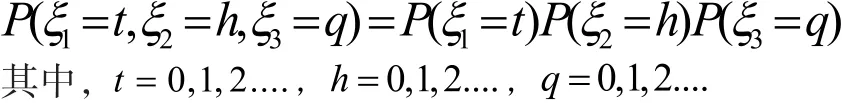
第二，规模化电动汽车的年用电量

求规模化电动汽车年用电量只与1）中充电电量ζ3的分布有关，记N为车辆总数，Q为年用电量

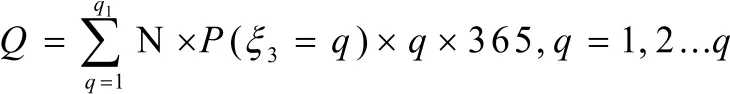
q1为从样本X观测出的充电电量的最大值，q1=40。通过MATLAB计算，填写附表1，如下

附表 1 规模化电动汽车的用电量

通过计算可以发现大约在上午十点大多数车辆开始充电，凌晨零点到六点开始充电最少，主要是因为多数人此时在睡觉。连接时长主要分布在0到10小时之间，这段时间是一般人的休息时间，超过这个时间之后就需继续工作。充电电量和连接时长的频率分布类似，主要是因为电动车的充电功率恒定，充电电量也就和充电时长正相关。

（二） 问题二的建模与求解

要求计算24小时的充电负荷曲线，并计算不同充电功率等级的比例，使得用户需求得到满足，减少设备投资，并降低电动汽车充电负荷的峰谷差。

第一，计算24小时充电负荷曲线。

充电负荷曲线是指电能用户的用电设备在某一时刻向电力系统取用的电功率的总和，将24小时平均分为96个时间段，每个时间段的时长为15min。记Lri为在第i时刻以第r级充电功率Nr辆车的充电功率和为车辆数，充电功率等级表如下表1

表 1 电动汽车充电功率等级

第r级充电功率下充电负荷曲线公式［2］为

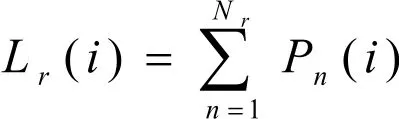
已知采取三个级别的充电功率的汽车比例，记为ωr，其中最终总充电负荷曲线的公式为

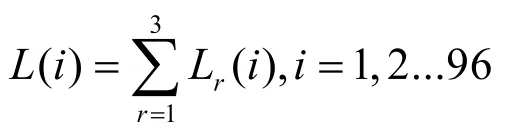
在本题中影响充电负荷曲线的因素有充电功率、充电开始时刻、连接时长，我们已按照充电功率分成三类来计算，因此因素只剩下充电开始时刻T和连接时长Tc。T和Tc对充电负荷的影响为

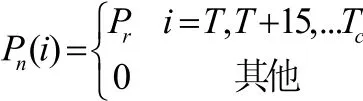
进而使用蒙特卡洛模拟仿真［3］的方法，根据充电开始时刻和连接时长的分布规律，来选取充电开始时刻和连接时长，进而算出充电负荷曲线。

第二，确定较优充电功率等级的比例。

本题为一个目标规划问题，题意中包含三个要求：满足用户需求、减少设备投资、降低充电负荷峰谷差。可将减少设备投资作为目标函数，即

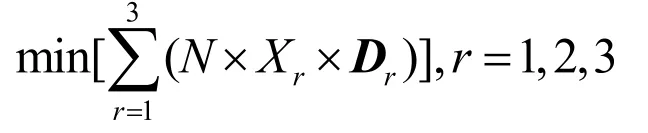
记N为车辆总数1万辆，Xr为新第r级充电功率等级的比例，Dr为第r级充电功率对应设备的成本。满足用户需求作为一个约束，可将该约束简化为1万辆车的总需求大于每辆车的平均充电量与1万辆的乘积，即

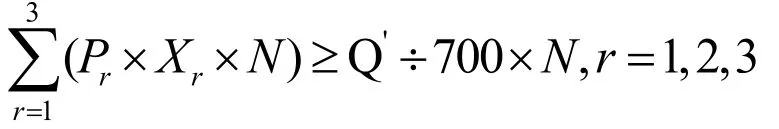
其中Pr为第r级充电功率的平均功率，Q'为充电量之和。

降低峰谷差，我们简化为降低峰值，根据1万辆电动汽车的充电负荷曲线，观测到峰值所在时刻为一天的第900分钟，即为15点钟，根据问题一所求充电开始时刻的分布规律，求得时开始充电的车辆数的概率［4］

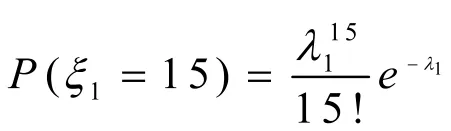
使得在t=15时的充电负荷小于第900分钟，也就是第i=60个时间段的充电负荷，求得约束

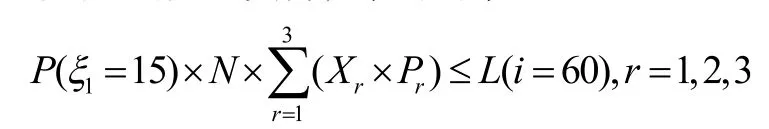
另外有

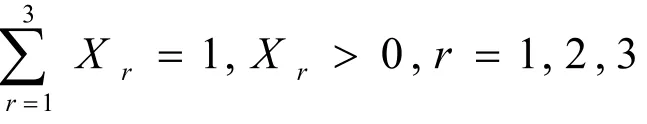
使用lingo求得

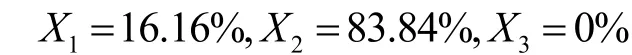
用MATLAB做出在该比例下充电负荷曲线，如下图6

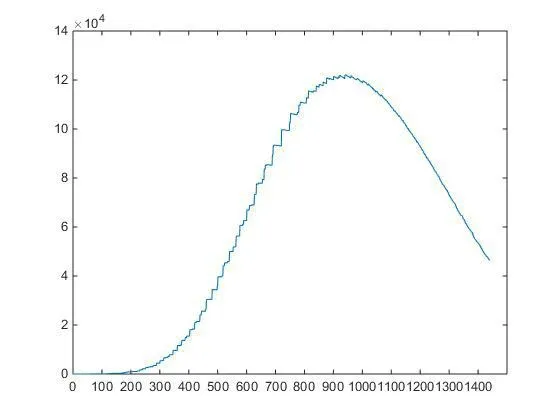
图 6 改进充电功率比例后的充电负荷曲线

（三）问题三的模型与求解

根据数据列出目标函数和约束条件，用lingo进行求解。

1．数据预处理。要求最大利润需先知道需求量和光伏发电量的关系，而每15分钟内的光伏发电量是已知的，就需要求出在此时间段内的需求量即充电电量。

首先在excel中对充电开始时刻进行排序，若该时刻在某一时间段内，则将其对应的电量累加到这一时间段内，直到所有时刻都进行完毕，共得到96组数据。

已知8台电桩最大功率为50KW，则在15分钟内的最大充电量为100KWh。若所得结果超过此数值，将其超出部分加到下一时间段内继续充电。

2．计算光伏全额利用时的最大利润。由于本题要确定是否需要购电和售电，就要根据发电量和需求量的关系建立一个0-1变量，来确定利润的组成。

目标函数：

最大利润=售电电价*剩余电量-购电电价*缺少电量+充电电价*需求电量

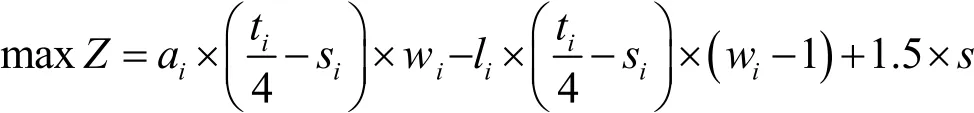
约束条件：

当光伏电量大于需求电量时，0-1变量值为1；当光伏电量小于需求电量时，0-1变量值为0

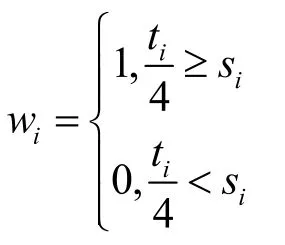
求解结果：最大利润为1367.527

3．计算允许弃光时的最大利润。本题与第一问相比只需去掉售出电量所得利润。

目标函数：

最大利润= -购电电价*缺少电量+充电电价*需求电量

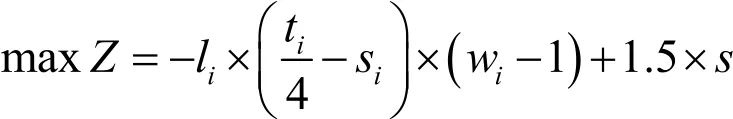
约束条件：

当光伏电量大于需求电量时，0-1变量值为1；当光伏电量小于需求电量时，0-1变量值为0

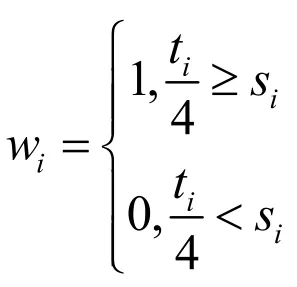
求解结果：最大利润为1255.355

（四）问题五分析

通过上述分析，使用蒙特卡洛模拟仿真的方法，根据充电开始时刻和连接时长的分布规律，来选取充电开始时刻和连接时长，进而算出充电负荷曲线。进一步调整比例，以降低电动汽车无序充电负荷的峰谷差。利用新能源充电站，通过对不同充电时段划分进行优化，实现了电动汽车的优化充电；讨论光伏的全额利用和允许弃光两种情况，优化出了24小时充电站的最大利润。

第三问主要展现了电网与新能源发电站的双向信息交流，使得充电站根据用户的需求、不同阶段的电价水平、光伏的利用情况与电网进行电量的双向交流，在合理利用的情况下，使得新能源充电站的利润达到最高。

由此可见，电动汽车可为电网提供多种改善服务，这些服务主要包括参与系统削峰填谷与新能源发电联合运行等。

随着科技的发展，汽车尾气污染的日益严重，电动汽车的将成为一种趋势，未来将有大量的电动汽车充电站，大量的电动汽车无序接入电网进行充电，将对电网的运行和规划方面产生较大的影响和改变，根据充电行为对充电负荷曲线进行研究，优化降低峰谷差，对电网的运行状态有重要意义。新能源充电站在与电网进行联合规划时达到尽量大的盈利性，将成为未来新能源发展的极为重要的一部分。

六、模型的评价

模型优点：

第一，利用MATLAB对数据进行处理，并画出相应图像，简单、直接、快捷。

第二，利用蒙特卡洛模拟仿真的方法，对电动汽车的行为进行分析。综合了各个特征量的分布规律，分析更具客观性。

第三，对不同时段充电进行优化，根据不同用户的需求、不同时段的电价水平，实现了新能源充电站电动汽车的优化充电。

模型缺点：

第一，问题一中忽略了连接时长、充电电量之间的相互关系，偏离实际情况。

第二，问题三中约束条件太过于简化，未能充分反应新能源充电站和电网之间的相互信息传递。

七、模型的推广

仔细分析各题所建模型，对未来电动汽车的发展有良好的辅助作用。联系电动汽车对电网进行规划可有助于未来新能源充电站的建立和合理利用。通过减少峰谷差减少电动汽车无序充电对电网的损害，利用优化模型优化出不同条件下的充电站最大利润，对未来新能源充电站的发展是一大机遇。未来将有大量电动汽车面向社会，根据我国的具体交通数据，通过所建立的无序充电模型，构建出适合我国的无序充电模型，及充电站和电网的交互。