考虑刷丝变形的后夹板结构对刷式密封泄漏和传热特性影响的研究

2019-09-10马登骞张元桥李军晏鑫

西安交通大学学报 2019年9期

马登骞,张元桥,李军,晏鑫

(西安交通大学叶轮机械研究所,710049,西安)

刷式密封作为一种先进动密封技术在透平机械中得到了广泛应用[1]。刷式密封主要由前夹板、刷丝束以及后夹板3部分组成,典型刷式密封的结构示意图如图1所示,刷丝束由前夹板进行固定,由后夹板对其产生支撑作用。在刷式密封运行过程中,刷丝束受到泄漏流、转子以及后夹板的共同作用会产生变形和磨损,发生刷丝悬挂、刚化效应和摩擦热效应等。在泄漏流体的压力作用下,刷丝束与后夹板间的作用力使刷丝束不能及时跟随,出现刷丝悬挂,进而产生刚化效应,降低封严性能[2]。而且,刷式密封的摩擦热效应会进一步加剧刷丝的磨损,同时在转子表面及刷丝顶部产生局部高温区,不利于转子及刷式密封的稳定运行。

科研人员采用实验测量和数值模拟方法,研究了刷式密封的泄漏特性、力学特性以及传热特性,旨在掌握刷式密封泄漏特性变化规律和刷丝束刚化、摩擦热效应的作用机制。Turner等通过实验测量了单级刷式密封径向间隙分别是0.27、0.75 mm时的泄漏量以及后夹板径向、转轴的轴向压力分布,实验研究表明刷丝束产生的闭合效应提高了密封性能[3]。孙晓萍等指出,在进行刷式密封设计时刷丝束与转轴间应采用小的间隙或小的过盈配合[4]。Deville等通过实验获得了过盈配合下刷丝束及转子表面的温度分布,发现高温分布区主要集中于刷丝束顶部[5]。

Bayley等提出了线性Darcian多孔介质模型,用于预测实验研究的刷式密封泄漏量[6]。Li等发展了计算刷丝对流体的黏性力及惯性力的理论模型,将刷丝束处理为具有各向异性阻力系数的非线性多孔介质模型,数值研究了实验测量的刷式密封泄漏特性,验证了理论模型的有效性[7-8]。Dogu等基于多孔介质模型,数值研究了刷丝束以及前后夹板等结构参数对泄漏特性的影响,发现相较于其他结构参数,密封间隙对泄漏量的影响占据了支配地位[9]。Hendricks等建立了刷丝束接触力分析模型,考虑了刷丝干涉量、气动力对刷丝顶部接触力的影响,但该模型忽略了刷丝之间的摩擦作用[10]。Li等基于悬臂梁理论对刷丝的力学特性开展了研究,但该理论忽略了刷丝之间的相互作用[11]。孙丹等基于流固耦合模型,研究了刷丝变形特性和力学行为对刷式密封泄漏特性的影响[12]。

虽然很多学者对刷丝束力学特性进行了研究,但未充分考虑刷丝与前后夹板之间以及刷丝之间的相互作用,关于流动与刷丝变形以及传热特性的耦合数值研究鲜见报道。因此,本文采用基于非线性Darcian多孔介质模型的RANS方程,耦合有限元分析(FEA)的非线性接触模型,建立预测刷丝变形以及摩擦生热的数值模型与计算方法,考虑了流体气动力、刷丝间摩擦力和刷丝与前后夹板间的相互作用,探究了不同后夹板结构对刷式密封泄漏特性、刚化效应和摩擦热效应的影响规律。

图1 刷式密封结构示意图

1 数值方法和验证

1.1 计算流体力学及FEA耦合计算流程

刷式密封泄漏特性、力学特性以及传热特性耦合计算流程如图2所示。采用计算流体力学(CFD)及FEA耦合计算研究泄漏气流对刷丝束变形、泄漏流场与传热特性的影响。根据刷式密封的实际结构参数建立相应的刷式密封泄漏流动的CFD模型和刷丝变形的FEA模型并生成初始网格,采用商用软件Ansys CFX进行数值计算,获得刷丝变形前气流对刷丝的气动力,利用Ansys APDL将气动力载荷输入到FEA模型中,进而求解刷丝变形量及刷丝与转子表面的摩擦力;采用UG NX参数化建模功能对CFD计算中的刷丝束多孔介质域重新进行几何建模,划分新网格,网格数量以及节点分布规律均与初始计算时的网格保持一致;进行刷丝变形后的CFD计算,求解新的气动力、刷丝变形量和摩擦力,进行迭代计算,当刷丝变形量及刷丝与转子面的摩擦力变化小于0.5%时,则认为整个计算过程收敛。

图2 CFD与FEA耦合计算流程图

1.2 非线性Darcian多孔介质模型

刷丝束的内部流动可简化为多孔介质内部流动。多孔介质模型是基于求解引入气流与刷丝之间阻力的三维RANS方程,即通过在RANS方程中引入阻力源项,包括黏性阻力项及惯性阻力项

(1)

(2)

式中:Ai、Bi分别为黏性阻力系数矩阵、惯性阻力系数矩阵。式(2)右端第1项为黏性阻力项,第2项为惯性阻力项,由于刷丝束结构的各向异性,采用非线性Darcian多孔介质模型定义阻力源项。黏性阻力系数及惯性阻力系数由转轴轴向X、与刷丝平行方向s、垂直刷丝方向n进行定义,3个方向的黏性阻力系数为aX、as、an,3个方向的惯性阻力系数为bX、bs、bn。

刷丝束的黏性阻力系数及惯性阻力系数受孔隙率及刷丝束结构的影响。孔隙率可表示为[13]

(3)

(4)

式中:Vb为刷丝体积;Vt为总体积;d为刷丝直径;N为刷丝束密度;D为转子直径;w为刷丝束厚度;r为刷丝径向位置;Φ为倾角;Dout为根部直径。

采用Ergun方程得到刷丝束内流动阻力系数[13]

(5)

式中:α、β为Ergun经验常数;μ为动力黏性系数;Dp为填充床内固体颗粒的平均直径,对于圆柱刷丝结构Dp=1.5d。根据式(2)～(5),可得3个方向的黏性阻力系数和惯性阻力系数[13]

(6)

(7)

as=0.4εan;bs=0

(8)

孔隙率和阻力系数可通过刷丝直径、刷丝倾角等刷式密封结构参数计算获得,刷式密封特有的结构决定了其在运行过程中,刷丝束厚度会随刷丝束上下游压差增大而减小,因此在数值计算过程中须对刷丝束孔隙率及阻力系数进行校核。在进行第一次CFD计算时,刷丝束初始厚度w0为2.17 mm。在气动力作用下刷丝会发生变形,沿径向方向刷丝束厚度会发生变化,进行FEA计算来提取刷丝束变形数据,之后采用Matlab CFTOOLS拟合刷丝束厚度w与径向位置r的函数,即

w=f(r)

(9)

阻力系数是孔隙率的函数,孔隙率发生变化时,相应的阻力系数也会发生改变。

1.3 计算模型和数值方法验证

单级刷式密封能承受的最大上下游压差为0.3～0.35 MPa,超过此压差时,需设计多级密封刷环。在多级密封刷环运行过程中,由于受到出口气流的冲击,下游刷丝束会发生较快磨损,之后磨损转移到上一级刷丝束,最终导致刷式密封的整体密封性能严重下降[14],因此需要设计耐高压、低刚化效应的先进刷式密封。本文采用数值方法研究3种后夹板结构的刷式密封在不同转速和压比下的泄漏量及刷丝束压力分布特性,如图3所示。图3中结构1是典型后夹板结构的刷式密封,结构2是在结构1基础上设计径向高度为8 mm的环形槽,结构3是在结构1的基础上设计径向高度为4 mm的环形槽。刷式密封各表面示意图和3种后夹板结构刷式密封的相同几何参数如图4、表1所示。

对于在结构上具有周向轴对称性的刷式密封,为了提高计算效率、合理利用计算资源,数值计算时沿转子周向方向选取1°部分作为计算域。计算域包括刷丝束上下游流体域、刷丝束多孔介质域、转子及夹板等固体域,采用Ansys ICEM对计算域进行结构化网格划分,计算域网格如图5所示。

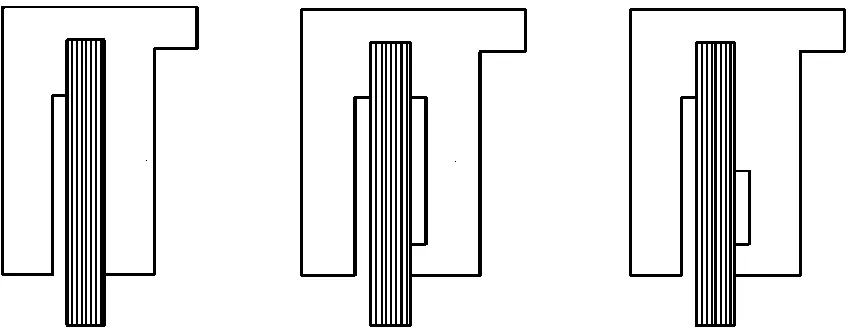
(a)结构1 (b)结构2 (c)结构3 图3 刷式密封结构示意图

图4 刷式密封各表面示意图

几何参数数值D/mm400d/mm0.15w0/mm2.17刷丝顶部倾角Φ0/(°)45刷丝束自由高度L/mm12.25刷丝束围栏高度H/mm2.55刷丝束干涉量Δ/mm0.2前夹板内径D1/mm405.1后夹板内径D2/mm405.1

图5 刷式密封计算网格

采用Ansys CFX进行数值计算,刷丝束计算域采用层流模型,刷丝束以外的流体域采用SSTk-ω湍流模型。边界条件与实验相同,进口给定总温、总压,出口给定静压,转子表面定义为旋转表面,给定转速,固体边界为无滑移边界,刷式密封计算边界条件如表2所示。

采用网格数分别为90万、110万、130万、150万的网格进行刷式密封泄漏特性数值计算的网格无

表2 刷式密封计算域边界条件

关性验证,通过刷丝束下游面沿转子径向方向的量纲一压力系数进行网格无关性验证。定义量纲一压力系数

(10)

式中:pd为刷丝束下游压力;pu为上游压力。量纲一径向位置r*=(r-D/2)/L,其中r为径向位置;量纲一轴向位置x*=x/w,其中x为轴向位置。

后夹板环形槽结构使刷丝束下游面压力发生一定波动,选用后夹板环形槽结构的刷式密封进行网格无关性验证,能更准确地反映压力波动变化。对于结构3刷式密封,Rp=2.3、n=3 000 r/min时,4种网格数量下压力系数随径向位置的变化曲线如图6所示,可知网格数达到110万时,沿径向的压力系数不再发生变化。由于网格数量相对较少、计算速度较快,为保证计算精度,3种后夹板结构的刷式密封均选用网格数为150万的网格进行计算。

图6 不同网格数量下刷丝束下游面沿径向的压力系数(结构3,Rp=2.3,n=3 000 r/min)

考虑、不考虑刷丝变形时,结构1刷式密封在转速为0、3 000 r/min工况下,数值计算泄漏量与实验泄漏量随压比的变化曲线如图7所示,实验数据由文献[13]获得。压比为1.0～1.5时,考虑、不考虑刷丝变形时的泄漏量基本相近。这是由于在压比较低时,刷丝变形量较小,对泄漏量的影响作用较弱。压比为1.5～2.0时,考虑、不考虑刷丝变形时的泄漏量均吻合较好。压比为2.0～3.1时,考虑刷丝变形的数值计算泄漏量与实验泄漏量吻合较好,而不考虑刷丝变形时的泄漏量则与实验泄漏量存在较大的偏差,最大相对误差为18.2%。实际运行工况中,刷式密封上游与下游间较大的压差会使刷丝束沿轴向方向被压紧,增大了流动阻力,考虑刷丝变形对泄漏量的影响符合实际物理现象。

图7 考虑、不考虑刷丝变形时数值计算泄漏量与实验泄漏量的对比

1.4 刷式密封有限元接触模型

(a)非线性接触模型单元划分

结构1 结构2 结构3(b)不同后夹板结构非线性接触模型图8 刷式密封非线性接触模型

采用Ansys APDL命令流建立刷式密封非线性接触模型,有限元模型如图8所示。刷丝均按照相同倾角呈交叉轴向排列,沿转子轴向方向的刷丝数量根据刷丝束厚度确定;考虑刷丝沿周向方向具有轴对称性,因此沿周向方向选取3排刷丝。刷丝之间的接触关系视为梁与梁平行接触,刷丝与转子表面之间的接触关系视为点与面接触,末排刷丝与后夹板表面之间的接触关系视为梁与平面接触。刷丝之间的摩擦因子μbb为0.2,刷丝与转子表面之间的摩擦因子μbr为0.24,末排刷丝与后夹板之间的摩擦因子μbp为0.28[15-16]。摩擦热的计算公式为

Qf=NtFfUR

(11)

式中:Nt为计算域刷丝数;Ff为单根刷丝所受摩擦力Ff的模;UR为转子表面线速度。

以文献[17]中刷丝束接触力实验中的刷式密封作为数值验证对象,验证本文所用有限元模型对计算刷丝与转子表面接触力的有效性,单根刷丝所受的接触力为

Fc=Ff+Fn

(12)

式中:Fn为单根刷丝所受法向接触力。计算域刷丝所受接触力数值之和可表示为

Fc-t=Nt|Fc|

(13)

刷丝束所受接触力计算值与实验值的对比如图9所示。当干涉量小于0.6 mm时,数值结果与实验测量值吻合较好;当干涉量大于0.6 mm时,数值结果略小于实验值。数值预测结果与实验数据吻合良好,验证了所建刷式密封接触模型的有效性。

图9 刷丝束所受接触力计算值与实验值对比

根据文献[18]中刷式密封摩擦热效应实验数值,对刷式密封传热特性研究方法进行验证,刷式密封几何结构与文献[18]一致。在不同刷丝束上下游压差下,刷丝束顶部平均温度数值结果与实验结果对比如图10所示。在不同刷丝束上下游压差下,数值计算温度变化趋势与实验数据吻合良好,数值计算温度与实验数据最大相差约15 K,验证了摩擦因子取值的可靠性以及基于有限元模型传热特性研究方法的有效性。

图10 不同刷丝束上下游压差下刷丝束顶部平均温度的数值结果与实验结果对比(Δ=0.1 mm,n=30 000 r/min)

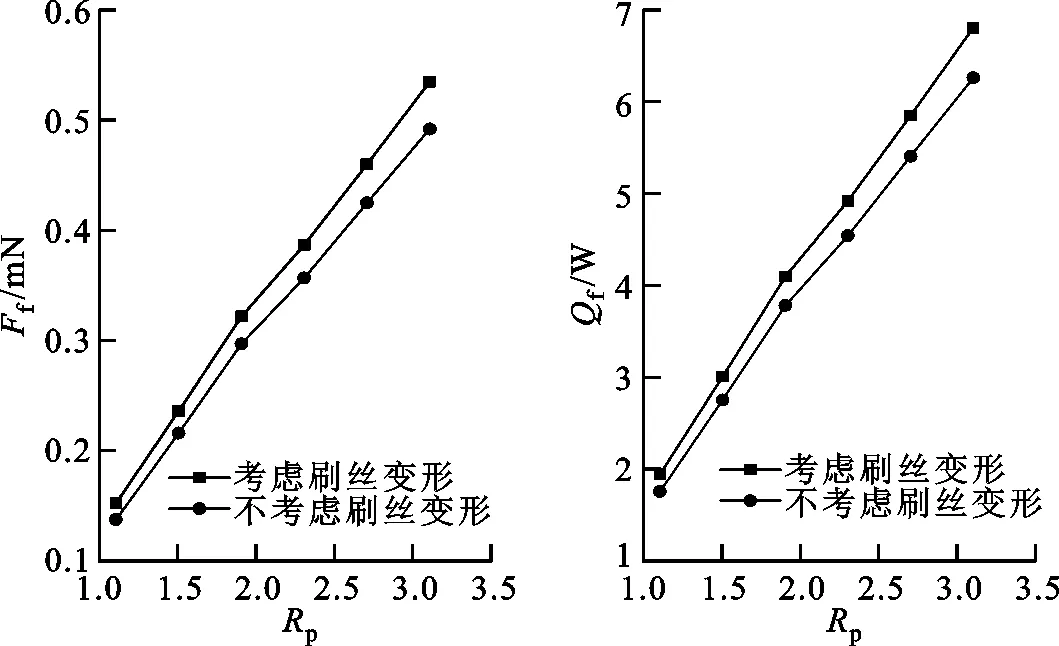
(a)单根刷丝所受摩擦力 (b)计算域刷丝摩擦热图11 考虑、不考虑刷丝变形时刷丝所受摩擦力及摩擦热对比(结构1,n=3 000 r/min)

考虑、不考虑刷丝变形时刷丝所受摩擦力对比与摩擦热的对比如图11所示,可知未考虑刷丝变形的摩擦力要小于考虑刷丝变形时的。实际运行工况下,刷丝束沿轴向方向被压紧,刷丝束刚度增加,刷丝与转子之间的摩擦力增大。本文采用的非线性接触模型考虑了由于刷丝束被压紧造成的摩擦力增大,与实际运行工况更为符合。随着压比的增大,两种情况下摩擦力的差异增大,这是由于:在低压比条件下,刷丝变形量小,摩擦力差异小;在高压比条件下,刷丝束被轴向压紧且变形量大,使得摩擦力的差异显著增大。考虑、不考虑刷丝变形的摩擦力最大差异为8.2%。摩擦热是摩擦力的函数,其变化规律与摩擦力的变化规律相近。

图12 考虑、不考虑刷丝变形时刷丝束下游面沿径向温度分布(结构1,Rp=2.7,n=3 000 r/min)

Rp=2.7、n=3 000 r/min,考虑、不考虑刷丝变形时,结构1刷丝束下游面径向温度分布如图12所示。由图12可知:在刷丝束顶部温度最高,之后呈指数减小,刷丝束顶部附近具有很高的温度梯度;考虑、不考虑刷丝变形时的温度差异主要集中于刷丝束顶部区域,两种情况下的最高温差约为10 K;在围栏高度以外的区域,两种情况下的温度曲线基本重合。

2 结果与讨论

采用基于非线性Darcian多孔介质模型的三维RANS方程,耦合FEA的非线性接触模型方法,研究了后夹板结构对刷丝束刚化效应的力学行为和传热特性的影响机制。

2.1 刷丝束变形时泄漏特性分析

n=3 000 r/min时,刷式密封泄漏量的变化曲线如图13所示。由图13可知:泄漏量随着压比的增大呈线性增大;结构1、2、3刷式密封的泄漏量随压比的变化基本一致,这是由于对于结构1、2、3刷式密封,气流仅从围栏高度内向下游泄漏;在相同压比下,转速变化对泄漏量影响较小;泄漏量随转速增大基本呈现先增大后减小的趋势。转子在旋转时,转子表面会对气流做功,使气流动能增大;气流内部存在黏性耗散作用,会将气流动能转化为内能。n为1 000～5 000 r/min时,泄漏量随着转速的升高略有升高,这是由于转子对气流做功的作用要强于气流内部中的黏性耗散;n为5 000～7 000 r/min时,泄漏量随着转速的升高略有降低,气流的黏性耗散作用要强于转子对气流做功。

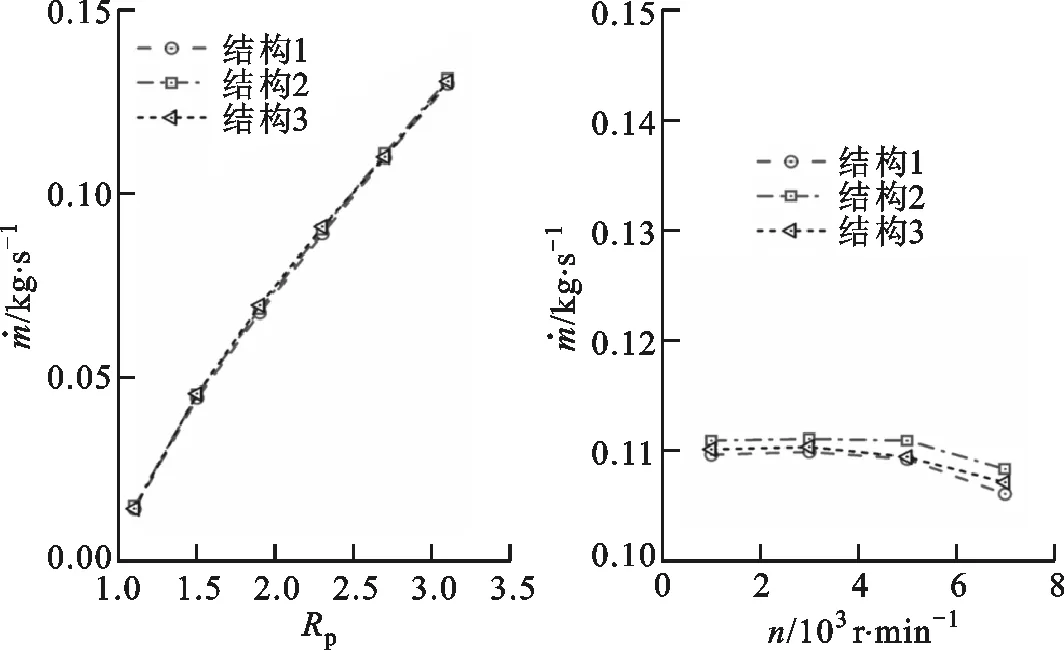
(a)泄漏量随压比变化 (b)泄漏量随转速变化图13 刷式密封泄漏量的变化曲线

2.2 泄漏流场

由于n=3 000 r/min为燃气轮机实际运行转速[19],为了获得在较大上下游压差条件下刷式密封的泄漏特性及刷丝束的压力分布特性,分析在较大压差条件下采用的3种后夹板结构对刷丝悬挂、刚化效应、刷丝变形以及传热特性的影响,本文选取Rp=2.7、n=3 000 r/min的工况进行研究。

(a)结构1

(b)结构2

(c)结构3图14 刷式密封静压及流线分布(Rp=2.7,n=3 000 r/min)

刷式密封压力场及流线分布如图14所示。由图14可知:对于结构1刷式密封,气流一部分沿轴向直接进入刷丝束,另一部分沿径向进入前夹板通槽后再进入刷丝束,气流在刷丝束中呈抛物线流动;在刷丝束上游附近,气流的离心运动较弱,气流很快发生转折并做向心流动;在刷丝束下游附近,气流向心流动明显,尤其是在后夹板底部区域,向心流动极其剧烈,气流明显的向心流动将刷丝束吹向转子表面,形成良好的闭合效应,密封能力增强;在后夹板底部区域,存在明显低压区,低压区卷吸下游气流,形成旋涡;对于结构2、3刷式密封,流动与结构1刷式密封相似,不同之处在于气流会沿径向进入后夹板环形槽,之后再沿径向进入刷丝束,在环形槽的角区,形成旋涡。刷丝变形对刷丝束内部的流场分布有一定影响,刷丝变形后末排刷丝与后夹板之间形成一个微小间隙,一部分泄漏气流流入末排刷丝与后夹板之间的间隙并沿着后夹板向转子径向流动,最终在围栏高度以下区域沿转子轴向偏转并流向下游区域。

压力在刷丝束上游区域及下游区域分布均匀。对于结构1刷式密封,压力在刷丝束中呈现环状分布:靠近刷丝束上游面附近压力变化不大;在刷丝束下游面的保护高度附近,压力急剧降低,具有很高的压力梯度,使得后排刷丝紧贴后夹板,发生悬挂,导致刷丝束易发生刚化效应。结构2、3刷式密封压力分布与结构1刷式密封类似,不同之处在于结构2、3刷式密封后夹板环形槽内压力分布与刷丝束上游分布相近,能平衡气流对刷丝的轴向作用力。

2.3 刷丝束静压分布

(a)刷丝束上游面及下游面沿径向压力系数

(b)刷丝束根部及顶部沿轴向压力系数图15 刷丝束表面压力系数分布(Rp=2.7,n=3 000 r/min)

3种后夹板结构的刷式密封刷丝束表面压力系数分布如图15所示。对于结构1、2、3刷式密封,刷丝束上游面压力分布与刷丝束上游区域压力基本相同。在结构1刷式密封中的下游面,自由高度以上区域压力与上游面基本相同,但从自由高度处沿径向指向转子方向,压力系数迅速减小,至围栏高度处压力系数为负值,结构1刷丝束上下游形成的巨大压差迫使刷丝束紧贴后夹板,刷丝在后夹板悬挂,易发生刚化效应。结构2、3刷式密封在后夹板设计了环形槽,环形槽内压力与刷丝束上游压力接近,在下游面,结构2环形槽内高压分布区约为结构3环形槽内高压分布区的2倍,且环形槽外径越大,环形槽内压力越接近刷丝束上游压力,在环形槽内径位置,压力发生骤降,结构2、3刷式密封能够有效防止刷丝悬挂,减弱刚化效应。

结构1、2、3刷丝束根部及顶部区域压力分布相近,刷丝束根部区域沿轴向方向压力基本不变,与上游压力相近,顶部区域压力沿轴向方向骤降。尤其是下游面,产生较大的径向压差,迫使刷丝改变倾角,与转子表面发生紧密贴合,增强密封作用。

2.4 刷丝束湍动能分布

实际工作中泄漏流的不规则运动会使刷丝发生扰动,尤其对于前排、后排刷丝,受到泄漏流扰动时发生变形的概率更大,湍动能是衡量泄漏流不规则运动的重要指标。

刷丝束上游面、中间面以及下游面沿径向湍动能分布如图16所示。由图16可知:上游面结构1刷式密封的湍动能在围栏高度以上发生剧烈波动,这是由于结构1刷丝束上游面以及下游面形成较大的压差,使泄漏流从上游面进入刷丝束的流动更为剧烈,增强了前排刷丝的扰动;结构2、3刷式密封湍动能约为0,中间面3种结构刷式密封湍动能为0,下游面结构2、结构3刷式密封湍动能在环形槽底部出现一个峰值,结构1刷式密封下游湍动能为0,结构2、3刷式密封能有效改善刷丝束中的泄漏流湍动能以降低不规则气流的扰动。泄漏流的不规则运动主要会使前排刷丝发生扰动,后夹板环形槽结构可减弱不规则泄漏流对刷丝的扰动,提高刷式密封运行的可靠性。

(a)上游面湍动能

(b)中间面湍动能

(c)下游面湍动能图16 刷丝束表面湍动能沿径向分布(Rp=2.7,n=3 000 r/min)

2.5 刷式密封刷丝束力学行为和传热特性

考虑刷丝变形时,计算域单根刷丝所受轴向、径向以及周向气动力随压比的变化规律如图17所示。由图17a可知,随着压比的增大,刷丝所受轴向气动力基本呈线性增大,压比大于2时,结构2、3轴向气动力略低于结构1。由图17b可知,结构1、2、3刷丝束所受的径向气动力沿径向方向向内,随着压比的增大,径向气动力增大,但增大趋势变缓,在高压比条件下,刷丝在径向气动力的作用下,会改变自身倾角并与转子表面发生贴合,形成良好的闭合效应。由图17c可知,周向气动力随着压比的增大,先减小,在到达某一压比后,周向气动力方向发生改变,并随着压比的增大而线性增大。

(a)轴向气动力 (b)径向气动力 (c)周向气动力图17 刷丝束所受气动力随压比的变化(n=3 000 r/min)

(a)首排刷丝 (b)中间排刷丝 (c)末排刷丝图18 刷丝轴向变形(Rp=2.7,n=3 000 r/min)

Rp=2.7、n=3 000 r/min时,在泄漏流气动力、刷丝束与转子面干涉量和前后夹板支撑力的共同作用下刷丝变形如图18所示。由于自由高度以上刷丝束由前、后夹板固定,轴向变形量很小。刷丝变形主要集中于围栏高度以下,因受到泄漏流气动力的作用,刷丝顶部向下游弯曲,最大变形量在0.03 mm左右,其中结构1的轴向变形量最大,结构2的轴向变形量最小。后夹板环形槽结构有利于减弱刷丝轴向变形,可以降低刷丝悬挂和发生刚化效应的可能性。

(a)单根刷丝所受摩擦力 (b)计算域刷丝束摩擦热图19 刷丝所受摩擦力及摩擦热(n=3 000 r/min)

n=3 000 r/min时单根刷丝所受摩擦力以及计算域刷丝束摩擦热如图19所示,刷丝所受摩擦力是轴向、径向以及周向3个方向气动力综合作用的结果。由图19a可知,对于结构1、2、3,单根刷丝所受摩擦力随压比的增大呈线性增大。这是由于:当压比增大时,泄漏流体作用在刷丝上的沿转子径向的气动力增大,导致刷丝与转子面间的接触增强,接触力增大;当压比增大时,作用在刷丝上的沿转子轴向的气动力增大,刷丝束发生轴向弯曲的同时排列更加紧密,刷丝与刷丝之间、刷丝与后夹板之间的接触增强,导致刷丝束的径向刚度增大,摩擦力增大。在较高压比条件下,结构2、3刷丝所受摩擦力略低于结构1刷式密封的,刷丝束计算域摩擦热与刷丝所受摩擦力成正比。

(a)结构1温度及流线分布

(b)结构2温度及流线分布

(c)结构3温度及流线分布图20 考虑刷丝变形时刷式密封温度分布(Rp=2.7,n=3 000 r/min)

Rp=2.7、n=3 000 r/min时刷式密封温度分布云图如图20所示。刷丝与转子摩擦热效应使刷丝顶部和转子表面附近区域的温度显著升高,摩擦热量沿径向以导热的方式向刷丝束的低温区域传递。由于泄漏气流在围栏高度以下区域进行膨胀加速并与刷丝发生强烈的对流换热,使得围栏高度以下区域的刷丝温度沿径向向外呈指数迅速下降,刷丝与转子干涉区域的温度更高,但是刷丝束围栏高度以上区域以及前后夹板的温升并不明显。这说明刷丝与转子交界面处摩擦热对围栏高度内刷丝束温度分布起主导作用,而围栏高度以上区域温度分布主要受到气流的对流换热的影响。在转子内部,摩擦热通过热传导向周围扩散,温度分布近似呈环形。

相比于结构1刷式密封,结构2、3刷式密封可以有效改善刷丝束以及转子内部的温度分布,减小高温分布区,减弱摩擦热效应对刷式密封运行产生的不利影响。