三维超声阵列风速风向测量方法

2019-09-10李新波朱阁彦李厚禹贾云龙

西安交通大学学报 2019年9期

李新波,朱阁彦,李厚禹,贾云龙

(吉林大学通信工程学院,130022,长春)

风是一种由许多在时空上随机变化的小尺度脉动叠加而成的自然现象,也是在大尺度规则气流上的一种三维矢量,主要包括风速、风向角和俯仰角这3个参数。作为一种很常见的自然现象,风的准确测量在工业、气象和航运等领域中,正发挥着越来越重要的作用[1-3]。近年来,基于超声检测的风参数测量技术越来越成熟,且与基于机械式、热敏式和激光多普勒式等的测风技术相比,具有无磨损、测量范围大和维护成本低等优势,因此被广泛关注[4-8]。在测风技术中,最常用的测风方法是时差法[9-11],即通过测量在顺风和逆风情况下,超声波信号在传感器发射端和接收端之间传播的不同时间来进行风参数的测量,因此基于时差法的测风仪器的测量精度完全取决于超声波传播时间的测量精度,但由于环境噪声的影响,想要通过仪器精准测量超声波传播时间并不容易。相对于平面风参数测量,国内外对空间三维风参数测量的研究较少。邓云逸等利用正四面体的超声波传感器阵列结构,并依据时差法的测量原理,分别测出水平面和垂直面的风速风向,然后通过矢量合成得到了空间三维风参数[12];Frank等通过联合安装在水平面和垂直面上的测风仪的测量结果,利用空间三维矢量合成计算出了三维风参数[13];Lopes等讨论分析了超声测风仪结构对测风精度的影响,并提出了一种几何结构非正交的超声测风仪,显著提高了基于时差法进行风参数测量的准确性[14]。但是,这些研究还是在基于时差法进行平面风参数测量的基础上,通过空间矢量的分解与合成计算出三维风参数,并没有克服基于时差法进行风参数测量的弊端。Li等在2015年提出利用阵列信号处理算法中的多重信号分类(multiple signal classification,MUSIC)的思想来计算风参数,该方法通过提取特征子空间和扫描功率谱来估计平面风参数,结果表明,所提方法相对于传统的时差法在抑制噪声和提高测量精度方面都有很大的优越性[15],但MUSIC算法需要对阵列接收信号进行奇异值分解[16],较大的计算量在一定程度上限制了实际应用中对系统实时性的要求。

本文将阵列信号处理中典型的波束形成算法应用到三维风参数测量领域,在计算量相对较小的情况下,实现了三维风参数的测量。首先,设计了一种空间超声波传感器阵列结构,并基于该结构分析了利用波束形成算法进行三维风参数测量的原理。然后,在Matlab软件中进行了所提测风方法的可行性实验及测量性能实验。最后,搭建了三维超声测风实验平台,对三维空间风进行了实物测量实验。

1 超声阵列结构设计及测风原理

1.1 超声阵列结构设计

三维超声测风装置结构如图1所示,主要包括超声波发射单元、超声波接收单元以及支撑单元。超声波发射单元包括1个超声波发射传感器,也称发射阵元,能在激励信号的作用下产生振动,发射出特定频率的超声波信号。超声波接收单元由8个超声波接收传感器(a1～a4,b1～b4)组成,每4个组成一组,分别安装在相互垂直的弧形支撑架上,用来接收发射阵元所发射的超声波信号,超声波接收传感器也称接收阵元,发射阵元和接收阵元是型号相同、且都具有收发一体化功能的超声波传感器。支撑单元是支撑架,用来连接、支撑和固定各个超声波传感器之间的相对位置。

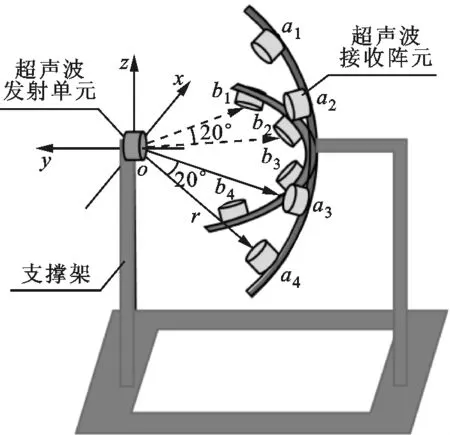
图1 三维超声测风装置结构图

由图1可知:处于垂直面yoz上的4个接收阵元a1、a2、a3、a4组成子阵列Aa,处于水平面xoy上的4个接收阵元b1、b2、b3、b4组成子阵列Ab,子阵列Aa和子阵列Ab共同组成该测风装置的传感器阵列A;在同一子阵列中,任意两个相邻的接收阵元与发射阵元之间连线的夹角为20°;发射阵元到各接收阵元之间的距离相等,即8个接收阵元在同一个以发射阵元o为圆心、r为半径的球面上。根据该测风装置的各阵元之间的相对结构可知:当无风时,从发射阵元发射的超声波信号同时传播到8个接收阵元;当有风时,超声波信号受风的影响,传播速度发生变化,从而到达各接收阵元的时间不一致。

1.2 基于波束形成算法的测风原理

超声波在空气中传播时,风速会在其声速上叠加,使超声波传播速度变快或变慢。因此,利用超声波传播速度和超声波声速之间的关系,便能测量出风参数[17]。

由于超声波声速c会受到传播介质的温度、湿度等因素的影响,因此有必要其进行修正来提高测风装置的测量精度[18]。目前,关于超声波声速与温度之间关系的研究较为成熟,工程上常用的表述温度T与超声波声速c之间的经验公式[10]为

(1)

本文用式(1)来修正超声波声速,下文中所使用的c即为修正之后的超声波声速。

空间风的来向可用图2表示,图中:V为风速;θ为风向角;φ为俯仰角,0°≤φ≤180°;α为在同一子阵列中的任意两个相邻的接收阵元与发射阵元之间连线的夹角,α=20°;Va为空间来风在垂直面yoz上的风速分量;Vb为空间来风在水平面xoy上的风速分量。根据空间几何分解的相关知识可知,Vb在水平面xoy上的分量如图3所示,Vb1～Vb4分别表示4个接收阵元方向的风速分量。

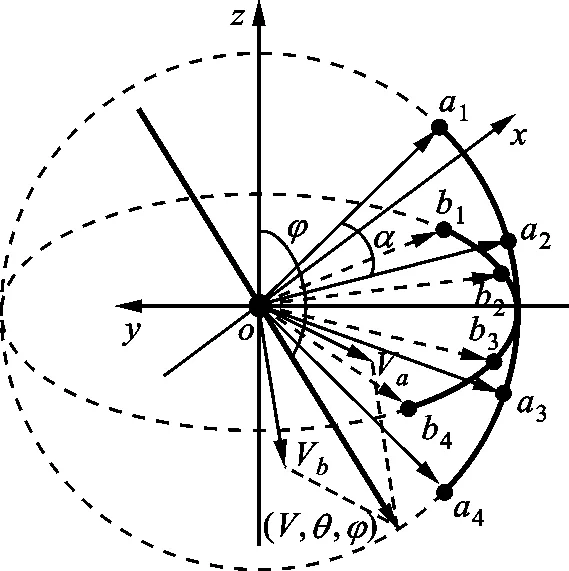
图2 空间风来向图

图3 Vb在水平面xoy上的分量示意图

空间风在xoy平面上各接收阵元方向上的风速分量可表示为

(2)

由于发射阵元所发射的超声波信号s(t)为单频窄带信号,因此可表示为

s(t)=u(t)ej[ω t+φ(t)]

(3)

式中:t为时间;u(t)为信号的幅度;φ(t)为信号的相位;角频率ω=2πf,f=40 kHz为信号的频率。

经过时间延迟τ之后,超声波信号可表示为

s(t-τ)=s(t)e-jωτ

(4)

子阵列Ab所接收的阵列信号xb(t)可表示为

(5)

式中:xbi为子阵列Ab中阵元bi所接收的超声波信号;nbi(t)为子阵列Ab中阵元bi上的空域采样噪声,且各阵元接收的噪声彼此独立;τi为超声波信号传播到阵元bi相对于传播到参考阵元的时间延迟,简称时延。

将式(5)以矢量形式表示,可以得到

xb(t)=s(t)Db+nb(t)

(6)

(7)

(8)

式中:Db为子阵列Ab的阵列流型矢量;nb(t)为子阵列Ab所接收的采样噪声的矢量形式。

超声波信号从发射阵元传播到子阵列Ab中的接收阵元bi(i=1,2,3,4)所需的时间ti可表示为

(9)

若将子阵列Ab中的接收阵元b4作为参考阵元,则时延可表示为

(10)

(11)

(12)

τ4=t4-t4=0

(13)

由以上分析可知,子阵列Ab的阵列流型矢量Db仅与时延τi有关,而τi是由空间风在平面xoy上的风矢量分量信息风速Vb和风向θ确定的,所以在超声波传感器阵列结构确定的前提下,子阵列Ab的阵列流型矢量Db直接由风速Vb和风向θ确定,即Db=Db(Vb,θ)。反过来说,确定了子阵列Ab的阵列流型矢量Db,也就确定了空间风在平面xoy上的风矢量分量信息风速Vb和风向θ。

根据波束形成算法中加权系数的常规确定方法可知,在空间阵列方向辨识应用中,若空间中只有一个来自方向为θk的信号s(t),其方向矢量为a(θk),则当加权矢量W取作a(θk)时,阵列输出为X(t)=WHs(t)=aH(θk)s(t),对其进行功率求解后得到的功率最大[19-20]。类比这种思想,可认为Db是风速风向矢量,当取加权矢量W=Db时,阵列输出为y(t)=WHxb(t),此时进行功率求解后功率最大。

根据常规波束形成算法,结合待估计参数为xoy平面上具有2参数的风速风向可知,子阵列Ab中各接收阵元所接收信号的加权输出为

(14)

将式(14)以矢量表示,可以得到

(15)

此时,子阵列Ab的阵列输出功率为

P(θ,Vb)=E[y2(t)]=WHRW=

(16)

式中矩阵R为子阵列Ab的阵列接收信号xb(t)的协方差矩阵,即

(17)

根据式(16),在Vb、θ分别处于0～60 m/s和0～359°的范围内,以确定步长遍历风速和风向,即可得到子阵列Ab的阵列接收信号的输出功率,其中最大功率所对应的风速和风向即为空间风在水平面xoy上的风矢量分量Vb和θ。

同理,对子阵列Aa接收的阵列信号做同样的处理,便能确定出空间风在垂直面yoz上的风矢量分量信息风速Va和风向φyoz,本节不再赘述。

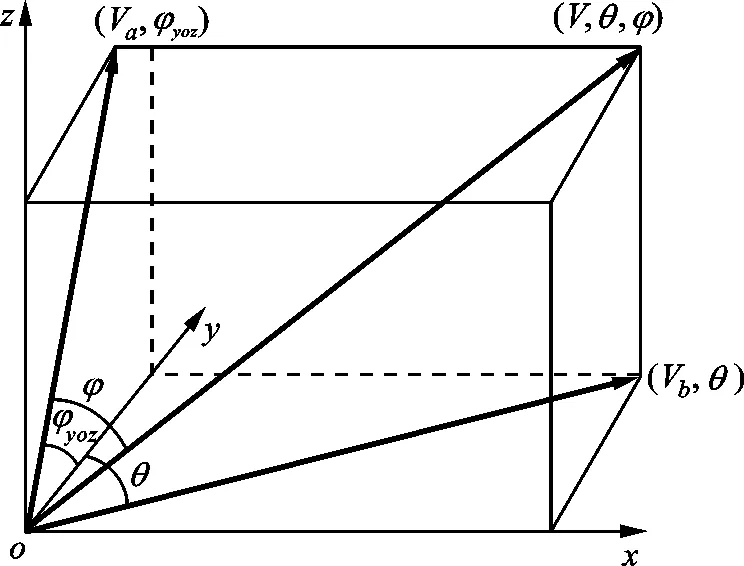
图4 空间三维风矢量的分解与合成示意图

图4是空间三维风矢量的分解与合成示意图,可以看出,在风参数矢量信息(Vb,θ)和(Va,φyoz)已知的情况下,球坐标系下的空间矢量(V,θ,φ)的终点在直角坐标系下x、y、z轴上的投影坐标可分别表示为

Vx=Vbsinθ

(18)

Vy=Vbcosθ=Vacosφyoz

(19)

Vz=Vasinφyoz

(20)

所以,球坐标系下的空间矢量(V,θ,φ)也可以在空间直角坐标系中表示为(Vbsinθ,Vacosφyoz,Vasinφyoz),该矢量的模为

(21)

空间风矢量的来向与z轴正方向之间所成夹角φ的余弦值可表示为

(22)

夹角φ可表示为

(23)

通过上述分析可知,在已知空间三维风矢量在水平面xoy和垂直面yoz上的风矢量分量信息(Vb,θ)和(Va,φyoz)时,便能确定出空间中的三维风参数,即风速、风向角和俯仰角。

2 仿真实验结果及分析

2.1 可行性实验

为了验证本文测风方法的可行性,在Matlab软件上进行了可行性仿真验证。首先,随机给出确定的空间风矢量在水平面xoy和垂直面yoz上的风矢量分量信息(Vb,θ)和(Va,φyoz),并计算出三维风参数(V,θ,φ)作为真实空间中三维风参数。然后,将子阵列Ab和Aa的阵列接收信号分别进行波束形成算法处理,得到2个相互垂直平面上的风矢量分量信息,并利用这2个风矢量分量信息计算出空间三维风参数,以此作为仿真结果。最后,将仿真结果与真实结果(V,θ,φ)进行比较,以此验证本文测风方法的可行性。

实验条件如下:模拟发射的超声波信号频率为40 kHz;发射阵元到各接收阵元之间的距离为r=10 cm;各接收阵元上的噪声为加性高斯白噪声;速度的扫描范围为0～60 m/s,步长为0.1 m/s;角度的扫描范围为0～359°,步长为1°。当快拍数为5 000、信噪比rsn=5 dB时,仿真结果如表1所示。

表1 三维风参数的真实值和仿真值

由仿真结果可知,当信噪比rsn=5 dB时,空间风的风速、风向角和俯仰角都能无差地估计出来。因此,可认为本文提出的方法是可行的。

2.2 成功率实验

由于存在环境噪声,估计结果相对于真实结果会有一定的偏差,为了验证本文方法的估计性能,设计了在不同信噪比下三维风矢量估计结果成功率的实验。由于速度扫描步长为0.1 m/s、角度扫描步长为1°,所以在该实验中,当速度估计的误差小于0.1 m/s、角度估计误差小于1°时,都认为估计成功。

实验条件如下:信噪比rsn的取值范围为-6～20 dB,步长为1 dB。在每个信噪比下做400次蒙特卡罗实验,分别估计可行性实验中的3组随机参数,结果如图5～7所示。

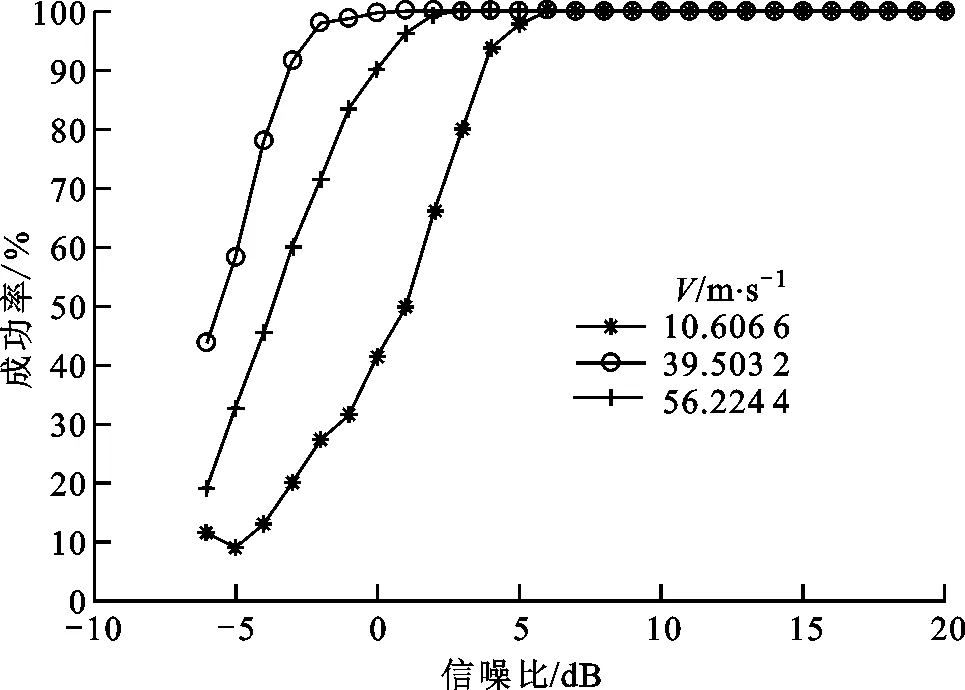
图5 风速估计成功率

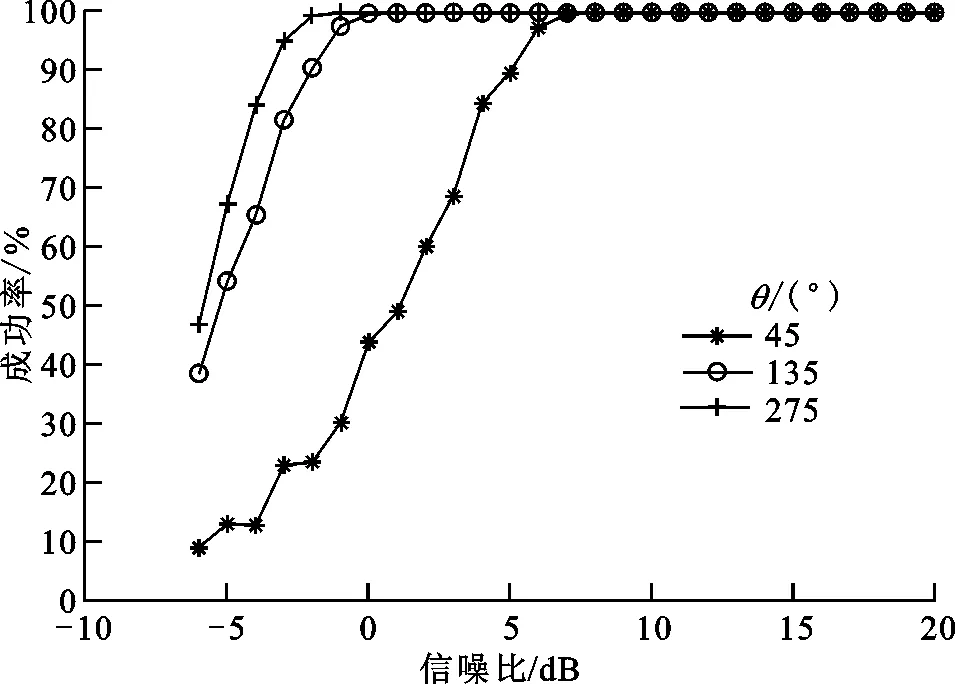
图6 风向角估计成功率

图7 俯仰角估计成功率

由仿真结果可知,在可接受误差存在的前提下,三维风参数的估计成功率随着信噪比的增加而增加,且在信噪比rsn≥5 dB时,成功率几乎达到100%。

2.3 均方根误差实验

为了讨论估计结果与真实结果的偏差度,设计了在不同信噪比的条件下,三维风矢量信息估计结果均方根误差RMSE的仿真实验,实验条件与2.2小节相同。均方根误差的公式

(24)

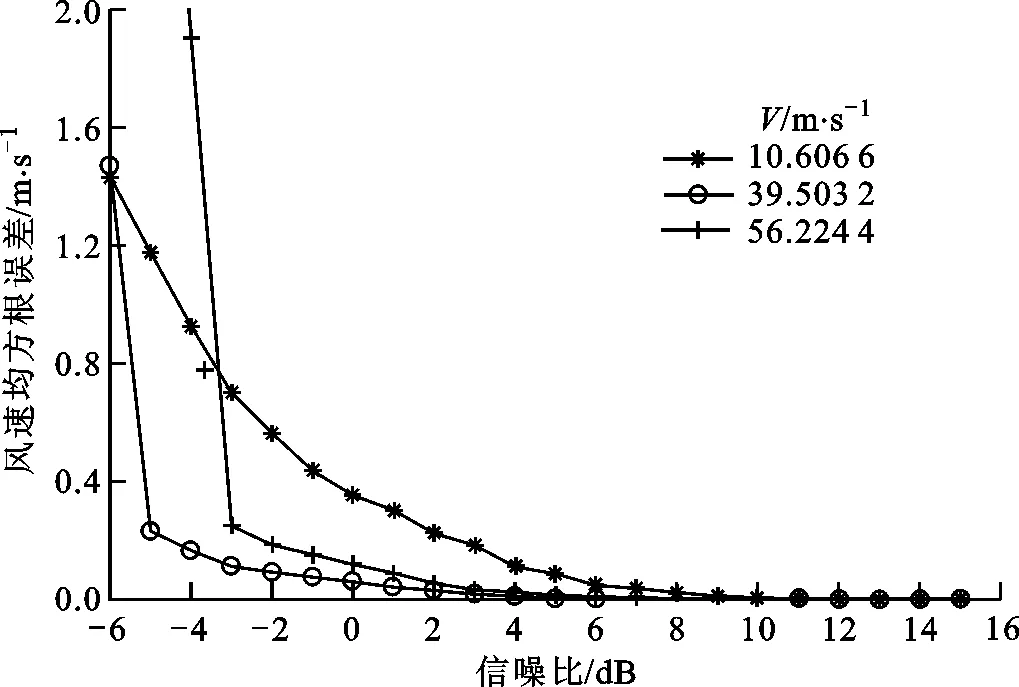
图8 风速均方根误差

图9 风向角均方根误差

图10 俯仰角均方根误差

由仿真结果可知:在低信噪比条件下,速度的估计效果好于角度的估计效果;随着信噪比的增加,三维风参数的估计结果越来越趋向于真值,在信噪比大于5 dB时,速度的均方根误差小于0.1 m/s,角度的均方根误差值小于1°。

通过以上3个仿真实验及仿真结果可知,本文所提的测风方法在理论上具有较好的三维风参数测量效果。

3 实验与结果

3.1 实验平台

为了验证本文提出的方法是否具有工程可实现性,搭建了基于超声波传感器阵列的三维风参数测量实验平台,如图11所示。直流可调稳压电源(HY3005ET)为风机提供稳定的电压,可调稳压电源(HSPY-200-02)作为控制单元(ATMEGA328P)的电源,使控制单元发送频率为40 kHz的脉宽调制,并通过驱动电路驱动发射阵元发射频率为40 kHz的超声波信号。风洞的整体框架由透明的亚克力板制作而成,如图12所示。当测风装置置于风洞中时,发射阵元发射的超声波信号在空气中传播会受风的影响,从而传播速度发生变化,所以超声波信号在发射阵元和接收阵元之间的传播时间就会发生变化,具体表现为接收信号之间相位差的变化。本实验采用4通道同步采样的示波器(MSO7054B),同步采样频率为20 MHz,每路信号最多可同时采集1 000个离散的数据点,保存成.csv格式的文件。

图11 三维风参数测量实验平台

图12 实验风洞

3.2 风洞中的风参数测量实验

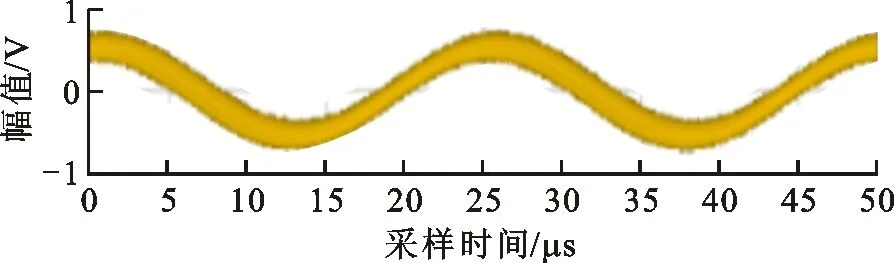
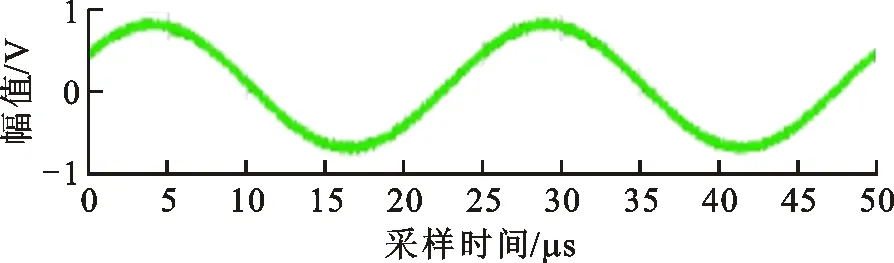
在采集信号之前,需要先将测风装置校准,使同一平面上4路通道所接收的信号在无风时保持同相。但是,由于没有精确的安装技术,在人为固定各超声波传感器的过程中,会存在较大的安装误差。经过一系列的结构调整和校准,无风时水平面4路接收信号在示波器上显示的波形如图13所示,可以看出,最终只能达到接收阵元b2、b3所接收的信号保持同相的水平。同时,在垂直面上只能保证接收阵元a2、a3所接收的信号保持同相。此时,接收阵元b2、b3、a2、a3接收的信号如图14所示。因此,在后续的实验过程中,只利用接收阵元b2、b3、a2、a3所接收的数据进行运算。

(a)阵元b1

(b)阵元b2

(c)阵元b3

(d)阵元b4图13 无风时水平面4路阵元接收信号的波形

(a)阵元b1

(b)阵元b2

(c)阵元a2

(d)阵元a3图14 无风时接收阵元b2、b3、a2、a3接收信号的波形

(a)阵元b1

(b)阵元b2

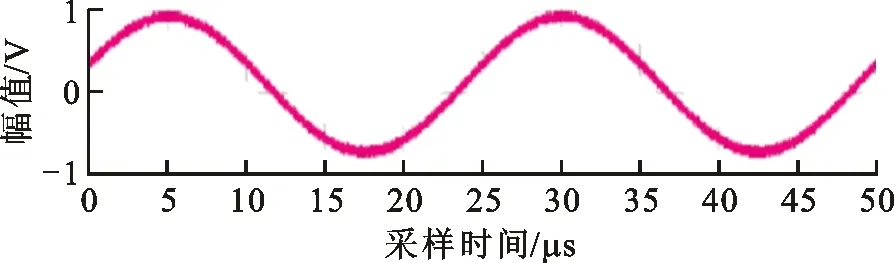
(c)阵元a2

(d)阵元a3图15 有风时接收阵元b2、b3、a2、a3接收信号的波形

有风时接收阵元b2、b3、a2、a3接收的信号如图15所示,可以看出,阵元b2、b3接收的信号和阵元a2、a3接收的信号之间出现明显的相位差。利用Matlab软件调用有风时的采样数据.csv文件,便能计算出风洞中的三维风参数。测量环境的温度为14.9 ℃,根据式(1)可得此时的超声波声速c=340.323 6 m/s,利用该修正后的超声波声速及采样数据,计算可得测量的风洞中的三维风参数,结果如表2所示。考虑到超声测风装置的安装误差以及实物实验测量中使用的接收阵元数量减半等因素的影响,超声测风装置测量的三维风参数相对于真值会不可避免地存在误差。由于风洞中风场的不稳定性和时变性,很难获得某一时刻风参数的真值,因此可通过借助市场上的测风仪来测量风洞中风速的最大值,进行本文方法可行性的验证。由于采用机械式测风仪(SMART SENSOR AS8556)测量的风洞中最大风速为6.443 m/s,所以当本文实验平台测量的风速小于6.443 m/s且在其附近时,便认为是合理的。本文实验平台所测风速为6.363 7 m/s,与机械式测风仪测量结果仅相差0.079 3 m/s,因此本文所提测风方法是具有工程实现性的。风向角和俯仰角会因测风装置所处的位置和风洞中气流的变化而变化,所以本节不讨论。本节仅说明本文方法具有工程实现性,更精确的测量需要更专业的仪器在更高规格的实验室或机构中进行。