一种采用2级反向传播神经网络的输电线路故障测距方法

焦在滨,宋新尧,李炳绪,吴润东

(1.西安交通大学电气工程学院,710049,西安;2.西安交通大学陕西省智能电网重点实验室,710049,西安;3.国网安徽省电力有限公司经济技术研究院,230022,合肥)

长距离输电线路故障的快速准确定位对于减轻巡线负担、快速恢复故障、保障电力系统的安全运行具有重大意义[1]。目前的故障测距方法按照原理不同可分为故障分析法和行波法这2类。故障分析法包括阻抗法、解复数方程法和电压法:阻抗法根据测量得到的电压和电流计算阻抗从而得出故障距离,受过渡电阻的影响较大[2-3];解复数方程法建立电压和电流的复数方程,通过迭代求解方程得出故障距离,计算量较大且容易出现伪根[4];电压法根据电压沿线路的分布规律求出故障距离[5]。行波法根据测量观测点和故障点之间的行波传播时间来计算故障距离[6],虽然具有较高的测距精度,但需要额外投资专门的一次传感器,且应用于高阻故障时可靠性问题较为突出。根据使用到的电气量来源,故障测距又分为单端测距法和双端测距法:单端测距法仅使用单端电气量,存在原理性误差[7-8];双端测距法可以消除原理性误差,但对同步性的要求较高[9-10]。过渡电阻是影响故障测距的关键因素,在高阻接地故障下,如阻抗法等的传统测距方法已经失效,解复数方程法、双端测距法等方法虽能够消除过渡电阻的影响,但具有运算较复杂、有伪根、对同步性要求高等不足。

提升测距算法的鲁棒性是故障测距研究的关键问题。鲁棒性是自动控制领域里的一个常用术语,表达在有外界扰动的条件下,系统保持稳定性和其他性能的能力[11]。国内外学者对各个外界因素的变化对测距方法的影响均展开了深入的研究,例如:线路参数发生变化[12]、两端数据不同步[13]、系统运行方式发生改变[14]等。但是,现有文献均未考虑到电气量数据测量误差对测距结果的影响。在实际电力系统中,测量误差是随机的、客观存在的,无法用统一的表达式进行表示,传统的以解析法为基础的测距算法无法从原理上将其避免。

神经网络经过充分训练后可以逼近任何期望的数学模型,作为一种新兴智能算法在故障测距领域已有一定的研究。文献[15-16]基于多层次反向传播(BP)神经网络,对单端多维电气量进行数据融合、计算故障位置,但由于未对电气量的变化特性进行充分研究,存在着输入电气量维度大、网络训练复杂、只适用于小电阻故障的不足之处。文献[17]对神经网络的结构进行了研究,提出了适用于故障定位问题的最优网络结构,但文中的训练样本集没有覆盖完整的故障模式空间,仅考虑了小过渡电阻接地的情况,因此训练得到的故障测距模型不能适用于各种故障模式。充分利用神经网络在模式识别及非线性拟合等方面的优势,可以解决现有故障测距方法的诸多不足,提出一种适用于各种故障模式的故障测距神经网络模型具有重要意义。

本文提出了一种基于2级BP神经网络的输电线路故障测距方法。首先,分析了双端电气量随过渡电阻的变化情况;然后,据此将故障场景分为低阻区和高阻区2类,构建了基于过渡电阻分类的2级测距神经网络;最后,对训练方法进行改进,将无误差和考虑误差样本组成的重复样本对作为BP神经网络的训练输入样本,使得训练后的测距网络对随机误差具备一定的适应能力。电磁暂态仿真结果表明:本文方法能够很好地解决高过渡电阻对故障测距准确性的影响,对随机误差的适应能力明显优于已有测距方法。

1 基于重复样本对训练的2级测距BP神经网络

1.1 双端电气量随过渡电阻的变化情况

过渡电阻是故障场景的一个关键属性,也是影响测距精度的重要因素。对于同一条输电线路,故障位置相同但过渡电阻不同时,双端电气量也会不同。

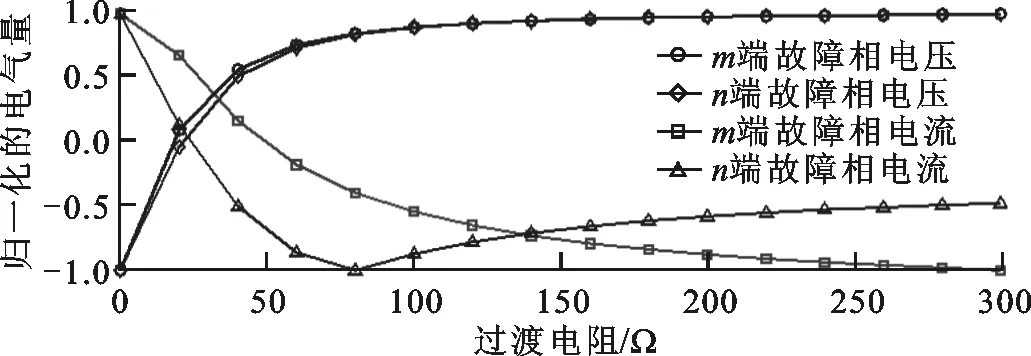
基于文献[18]中的500 kV典型京津唐输电线路模型及参数,对线路首端5 km处发生各种类型故障时双端故障相电气量随过渡电阻的变化情况进行电磁暂态仿真,结果如图1所示。

(a)单相接地故障

(b)两相短路故障

(c)两相接地故障

(d)三相接地故障图1 各故障类型电气量随过渡电阻的变化情况

由图1可见,输电线路双端电气量的变化规律与过渡电阻直接相关,以单相接地故障为例,可以分析得出以下结论。

(1)在过渡电阻较小(0～50 Ω,以下简称为低阻区)时,随着过渡电阻的变化,电气量变化迅速;在过渡电阻较大(50～300 Ω,以下简称为高阻区)时,随着过渡电阻的变化,电气量变化较缓慢。

(2)n端故障相电流在低阻区随过渡电阻的增大而减小,在高阻区随过渡电阻的增大而增大,呈现出完全相反的变化规律。

由此可以看出,输电线路双端电气量的变化规律与过渡电阻密切相关,呈现出显著不同的区域性特征。

由图1可知,虽然对于不同故障类型,区分其低阻区和高阻区的阈值不尽相同,但针对所有故障类型,输电线路双端电气量的变化规律均与过渡电阻相关,呈现出明显的区域性特性。为解决过渡电阻对于故障测距精度的影响,本文以过渡电阻为依据构建2级BP神经网络结构,从而实现输电线路的精确测距。

1.2 2级测距BP神经网络的基本原理

对于神经网络,在训练样本的规律过于复杂、训练样本的数目又十分有限的情况下,训练出的神经网络是难以精确反映训练样本的变化规律的。相反,训练样本数据的变化越有规律可循、变化的规律越单一、越简单,则训练网络对样本量的要求越低,训练效果越好。显然,对于一个具有不同变化规律的数据集,如果能够按照其变化规律将该数据集分成若干子类,则对各个子类分别进行网络训练的效果要远远好于对整个数据集进行网络训练的效果。所以,有必要将电气量数据分为高阻区和低阻区2个子类,对各个子类分别进行网络训练,以得到更好的训练效果。

本文构建的两级测距BP神经网络的基本原理如下:将归一化的量测电气量数据输入第1级分区网络进行阻抗分区,根据过渡电阻所在区域选择第2级测距网络,而第2级网络的训练集则分别考虑低阻区及高阻区的故障定位差异,其输出结果即为故障测距的最终结果。

(1)第1级BP神经网络:用于过渡电阻阻抗分区。原始双端电气量(m端电压和电流um、im,n端电压和电流un、in)经预处理后得到归一化的双端电气量,为第1级BP神经网络的输入,输出量Qsort表征输入数据位于高阻区或低阻区的概率(若Qsort≤0.5,则输入数据位于低阻区;若Qsort>0.5,则输入数据位于高阻区)。第1级神经网络要实现的映射关系为

(1)

(2)第2级BP神经网络:用于故障测距。第2级神经网络的输入同第1级神经网络,输出为故障位置d0。第2级神经网络要实现的函数映射关系为

(2)

图2为本文提出的2级BP神经网络的总体结构。在电气量数据输入到神经网络进行计算之前,需要进行线性归一化处理,去除数据的单位限制,将其转化为区间[-1,1]内的数值,便于不同单位或量级的指标能够进行比较和加权。线性归一化的转化函数为

(3)

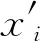
图2 2级BP神经网络的总体结构

1.3 重复样本对训练的基本原理

互感器的测量误差是影响电力系统故障测距精度的重要因素。电力系统电压和电流互感器的测量误差与诸多因素相关,具有随机性、不确定性、难以用统一的解析表达式描述等特征,目前的故障测距方法均无法从原理上避免互感器的传变误差对测距结果的影响。

与传统的基于解析法求解的测距算法相比,基于神经网络的测距方法的最大优势在于可以任意调整预期的数学模型,并根据模型选择相应的样本,然后对网络进行训练,使网络精确地逼近预期的数学模型。基于这一点,可以对训练样本做出如下改进:同时输入无误差样本集A和考虑误差的样本集B。样本集A中的数据即为仿真得到的电气量数据真值,样本集B中的数据是在样本集A的数据中重复性地加入随机噪声(测量误差)后得到的。利用样本集A和B的数据对神经网络进行训练,使得训练后的神经网络能够自动降低噪声干扰,在无误差和考虑误差的故障场景下均能精确计算故障位置。

对于同一个故障场景,将无误差样本集A和考虑误差样本集B中的训练样本组成的训练样本集定义为“样本对”。对于某一故障场景,样本对的定义为

(4)

由于测量误差是随机分布的,对于某一故障场景,仅用1组样本对训练显然是不够的。为了让网络能够充分识别各种测量误差,对于单个故障场景,本文选取的训练样本对的数量为100,重复训练100次,训练的样本对集合为

(5)

2 训练集的生成与BP神经网络调参

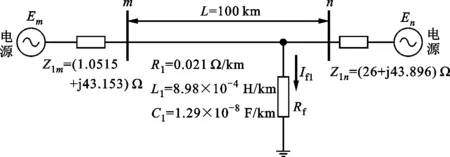
图3 输电线路正序等效电路图

图4 输电线路零序等效电路图

采用PSCAD/EMTDC电磁暂态仿真软件对输电线路模型进行仿真,获得训练的原始数据样本。采用Matlab软件进行数据处理,采样频率为2 kHz,利用全周傅式算法提取工频相量,计算得到双端电压和电流的幅值和相角。

2.1 故障场景的选择

训练样本应涵盖各种故障特征,需要选取合适的、具有代表性的故障场景作为研究对象。生成训练样本时,应考虑以下因素:

(1)500 kV线路上发生故障后,最大的过渡电阻可达300 Ω,所以取过渡电阻的区间为[0,300] Ω;

(2)故障位置采用归一化后的值,即实际故障位置和线路总长的比值,取值范围为[0,1];

(3)线路两端电势夹角分别取为15°、25°、30°、35°、45°;

(4)设对端系统阻抗的额定值为ZN,对端系统阻抗取为0.8ZN、ZN、1.2ZN。

考虑到低阻区电气量变化较快,故减小过渡电阻的变化步长,增加故障场景的数量。由于高阻区电气量变化较慢,较少的故障场景即可代表整个高阻区的变化特征。结合上述准则,确定故障场景集合如下。

低阻区:过渡电阻为{0,5,10,…,45,50}Ω,故障位置为{0,0.2,0.4,…,0.8,1},两端电势夹角为{15°,25°,30°,35°,45°},对端系统阻抗为{0.8ZN,ZN,1.2ZN}。

高阻区:过渡电阻为{60,80,…,300}Ω,故障位置为{0,0.2,0.4,…,0.8,1},两端电势夹角为{15°,25°,30°,35°,45°},对端系统阻抗为{0.8ZN,ZN,1.2ZN}。

对于第1级的高阻/低阻区域BP神经网络,准确分类对确保故障测距模型的精确测距尤为重要。该级神经网络的故障场景集合包含低阻区故障场景集和高阻区故障场景集,期望在低阻区输出量Qsort=0,在高阻区输出量Qsort=1。

利用选取的样本集训练BP神经网络,仿真结果表明训练后的神经网络能够达到以下精度:当过渡电阻R≤40 Ω时,输出量Qsort=0;R≥60 Ω时,输出量Qsort=1。但是,若过渡电阻在40～60 Ω的范围内,也就是处于高阻区和低阻区之间的过渡区域时,神经网络计算的Qsort在0～1之间。这种无法准确确定所属区域的过渡电阻范围(40～60 Ω)称为模糊区,即处于该范围内的过渡电阻可能被分入低阻区,也有可能被分入高阻区。

对于模糊区的处理原则如下:无论第2级网络是低阻故障测距网络还是高阻故障测距网络,所选取训练样本的故障场景都应完全覆盖模糊区,即对于处在模糊区内的输入数据,低阻区和高阻区的测距网络都可以给出准确的测距结果。所以,低阻区故障场景的过渡电阻调整为{0,5,…,55,60}Ω,高阻区故障场景的过渡电阻调整为{40,60,…,280,300}Ω。

经过组合,低阻区故障场景数为1 170个,高阻区故障场景数为1 260个。

2.2 测量误差的模拟

电压互感器和电流互感器的测量误差与其自身的设计参数和系统的运行工况等因素密切相关,目前尚无对互感器误差分布的研究数据,本节仅以互感器测量系统的随机误差为研究对象,说明神经网络训练集的生成原则和方法。

由于测量系统中随机误差的特点是小误差比大误差出现的概率大、正负误差出现的概率相等、误差的期望值为0、不同测量误差之间不相关,所以可以认为测量的随机误差为均值为0的高斯白噪声[19]。本文利用Matlab软件产生相应的高斯白噪声信号来添加到原始的工频电气量中,将处理后的工频电气量作为考虑测量误差的样本。

为研究加入不同强度白噪声后测量结果误差的分布情况,对某一电气量模拟测量700次,每100次测量为1组并加入相同强度的白噪声,研究该电气量在7种不同信噪比下的测量结果误差分布,结果如表1所示。

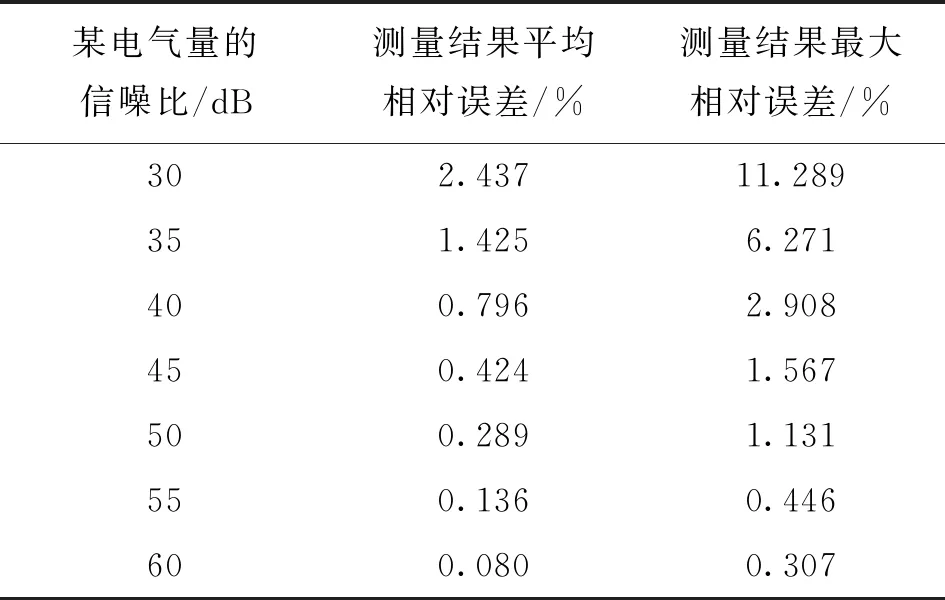
表1 某电气量在不同信噪比下的误差

由于电力系统中保护用电力互感器在系统短路工况下的测量误差一般不超过5%,根据表1,本文在该电气量训练样本中加入白噪声后,该电气量的信噪比范围应为40～50 dB。

2.3 2级BP神经网络的训练

训练前首先需要确定BP神经网络的结构参数。BP神经网络应用最广泛的激活函数有线性激活函数purelin函数、对数激活函数logsig函数、正切激活函数tansig函数。根据文献[17]的研究,用于故障测距的BP神经网络的最优结构应具备以下属性:

(1)输出层采用线性函数;

(2)其他层采用非线性函数;

(3)隐含层单元数一般是输入层单元数的2倍左右。

本文构建的2级BP神经网络共包含3个BP神经网络,根据网络的输入和输出数据的维度,确定BP神经网络的基本结构参数为:输入层节点个数为6,输出层节点个数为1,隐含层节点个数为16,输入层激活函数为tansig函数,输出层激活函数为purelin函数。

在生成的无误差训练样本集上加入白噪声,得到信噪比为50 dB的考虑测量误差的训练样本集,2级神经网络中的各个网络的训练情况如表2、表3及表4所示,表4中的绝对误差为实际故障距离与测量故障距离的差,相对误差为绝对误差与输电线路全长的商。

表2 第1级BP神经网络的训练参数

表3 第2级BP神经网络的训练参数

表4 第2级BP神经网络的训练性能指标

对于全部训练样本集,第1级BP神经网络能够准确地进行分类,误判样本数为0。误判样本指的是区域神经网络分类结果错误的样本,即本属于低阻区的样本被分类到高阻区,或本属于高阻区的样本被分类到低阻区。对于无误差训练样本集,第2级BP神经网络故障定位结果的最大相对误差小于1%;对于含有最大5%测量误差的训练样本集,第2级BP神经网络故障定位结果的最大相对误差为2.5%。由此可知,经过训练后的BP神经网络能够准确地逼近训练样本集对应的映射关系,网络的训练效果较好。

3 仿真验证

本文提出的2级测距BP神经网络应实现以下2个目标。

目标1:测距的准确性。输入电气量数据,神经网络经过运算后能够输出准确的测距结果。同时,训练后的神经网络需要对故障场景的变化(如两端系统阻抗的变化、两端电势夹角的变化等)具备一定的适应能力。此时关注的是神经网络测距的准确性,所以不考虑输入电气量数据有误差的情形,即输入的测试样本数据不含测量误差。

目标2:测距的鲁棒性。当输入电气量数据中存在一定的测量误差时,测距神经网络仍然能够给出较准确的测距结果。此时输入的测试样本数据应适当的加入测量误差。

本节针对以上2个目标,给出具体的仿真验证结果。

3.1 2级BP神经网络测距准确性的验证

本小节是对目标1的验证。所选取的测试样本一方面要覆盖各种故障特征,另一方面要与训练样本有差异以便验证神经网络的泛化能力。选取2组测试样本如下。

样本1:过渡电阻为{8,28,55,70,150,210,270}Ω,故障位置为{0.1,0.5,0.7,0.9},两端电势夹角为30°,对端系统阻抗为1.1ZN。

样本2:过渡电阻为{8,28,55,70,150,210,270}Ω,故障位置为{0.1,0.5,0.7,0.9},两端电势夹角为20°,对端系统阻抗为ZN。

样本1和样本2的测试结果如表5和表6所示。

表5 样本1的测试结果

根据表5可知,在对端系统阻抗发生变化的情况下,基于2级BP神经网络的测距方法不受故障位置和过渡电阻的影响,依然可以进行准确地故障测距,故障测距结果最大误差不超过1%。

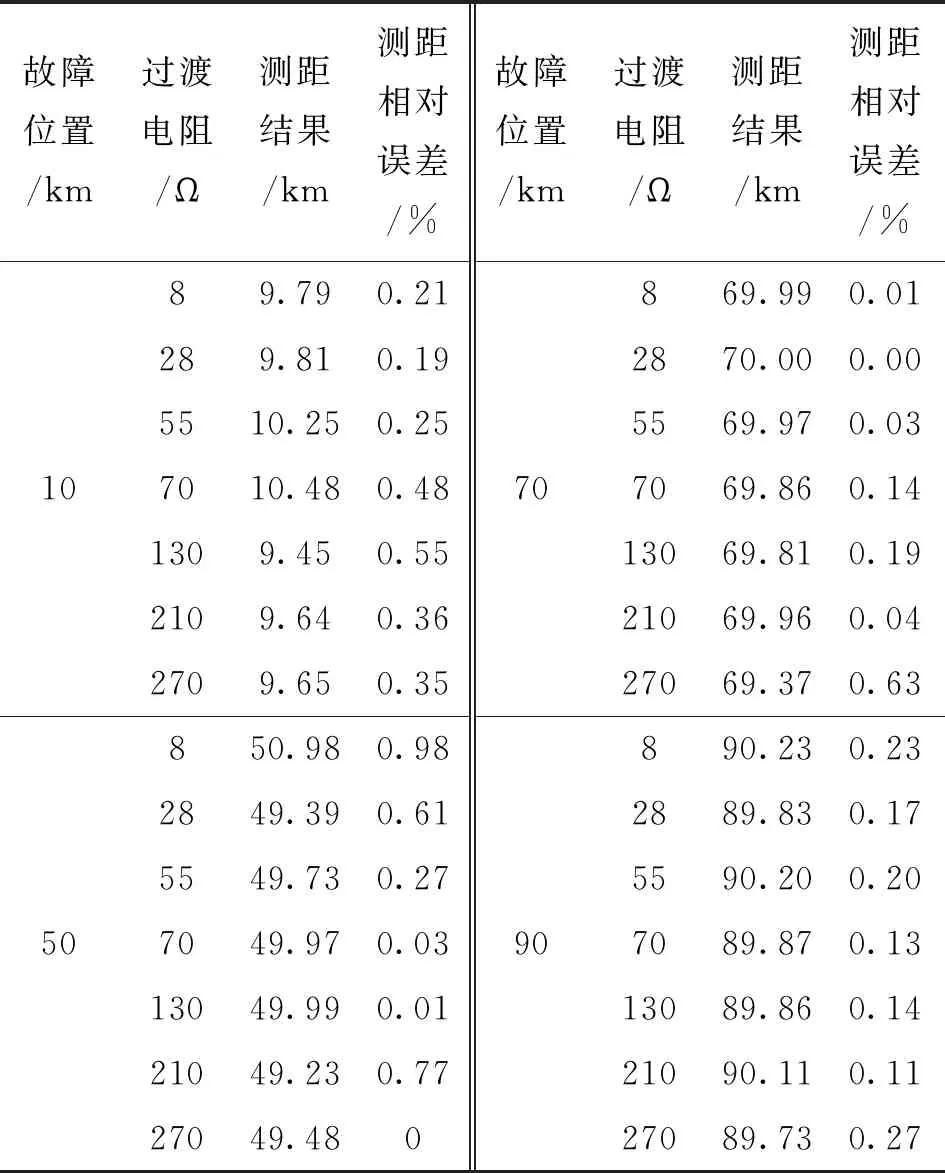
表6 样本2的测试结果

根据表6可知,当两端电势夹角发生改变时,基于2级BP神经网络的测距方法不受故障位置和过渡电阻的影响,依然可以进行准确的故障测距,故障测距结果最大误差不超过1%。即使对于高过渡电阻的故障场景,该方法仍然可以保证极高的测距准确度。

3.2 2级BP神经网络测距方法与解析法的鲁棒性比较

选取文献[20]提出的解析法与本文提出的测距方法进行鲁棒性比较。

文献[20]提出了基于解析法求解的数据融合故障测距方法。该方法利用线路两端距离继电器的测距结果和故障录波装置中的电气量数据,采用加权系数的数据融合方法,通过解析求解,对两端距离继电器的测距结果进行数据融合来获得精确的定位结果,仿真结果显示定位结果误差小于1%。

基于加权系数的数据融合方法建立的数据融合模型为

xfusion=αx1+βx2

(6)

式中:xfusion为融合结果;x1和x2为距离继电器的双端测距结果;α和β为融合系数。通过解析推导,用电流表示的融合系数的表达式为

(7)

采用全线搜索法来确定真实的故障位置,真实的故障位置是融合误差的唯一极小值点,融合误差E(x)的表达式为

E(x)=|xfusion-x|

(8)

式中x为故障位置到线路m端的距离。

用于对比的故障场景参数如下:过渡电阻为150 Ω,故障位置为0.45,共测量100次,每次引入不同的随机白噪声作为测量误差,测量电气量信噪比为50 dB。在该故障场景下对比解析法与本文方法的测距相对误差,结果如图5所示。

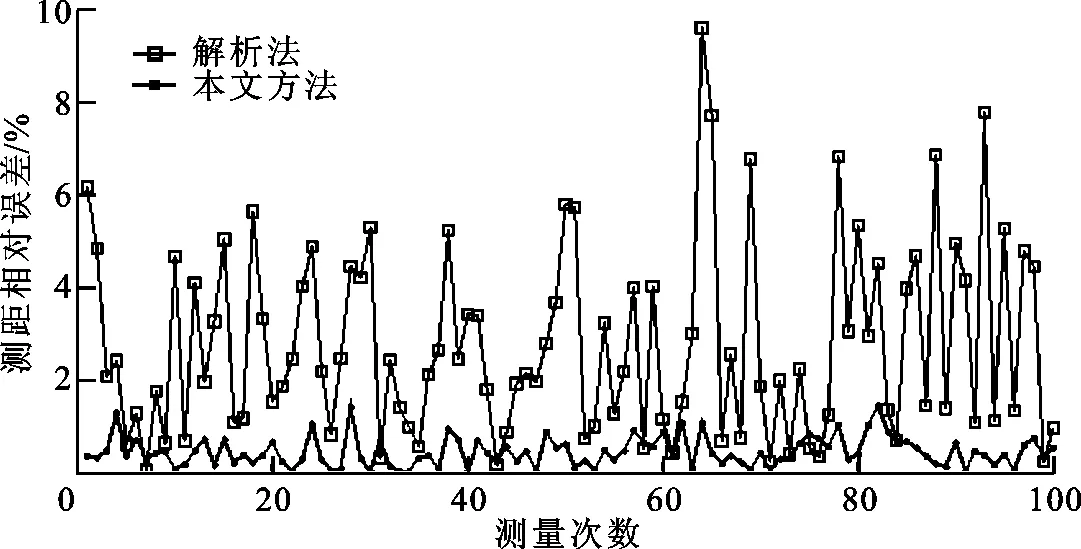
图5 解析法和本文方法的测距相对误差

由图5可知:在存在一定测量误差的情况下,利用解析法进行故障测距的误差较大,最大接近10%;本文方法的测距结果相对误差都在2%以内,鲁棒性明显优于对比方法。

根据仿真验证结果可知,本文提出的基于重复样本对训练的2级BP神经网络的测距方法不受过渡电阻的影响,可以实现高精度的故障定位。另外,基于重复样本对的训练方法显著提升了测距神经网络的鲁棒性,即使输入的电气量数据存在一定的测量误差,仍然能够给出精确的测距结果。

4 结 论

本文提出了基于重复样本对训练的2级BP神经网络故障测距新方法。在保证测距精度的同时较大地提升了测距算法的鲁棒性,理论分析和仿真实验表明,本文提出的测距方法具备以下优点。

(1)将故障场景根据电气量变化规律分为高阻区和低阻区两大类,分别进行神经网络的训练,在减少训练复杂度的同时提升了测距的精度,在过渡电阻很高的场景下仍然能够实现精确测距。根据过渡电阻大小进行分类的思想为今后输电线路故障测距的研究提供了新途径。

(2)由于测量误差的随机性,以解析法为基础的测距方法无法从原理上将其避免。然而,神经网络经过充分训练后可以逼近任何期望的数学模型,利用这一优势,本文对训练方法作出了改进:将无误差和有误差样本组成的重复样本对作为BP神经网络的训练输入样本,使得训练后的BP神经网络能够在输入的电气量存在一定的测量误差时,仍然能给出较为精确的测距结果。利用含误差的样本在训练中提升神经网络对随机误差的适应能力,也是一种提升故障测距精度的新思路。