柱棒式超磁致伸缩振动能量收集装置建模与实验

2019-09-10何忠波郑佳伟周景涛刘国平

农业机械学报 2019年8期

何忠波柏果郑佳伟周景涛刘国平

(1.陆军工程大学车辆与电气工程系，石家庄 050003； 2.32184部队，北京 100072)

0 引言

超磁致伸缩材料(Giant magnetostrictive material， GMM)是一种新型磁功能智能材料，可实现机械能-磁场能-电能之间的高效能量转换，与其他智能材料相比，其具有输出力大、应变大、滞环小、响应速度快、能量密度高等优点[1-3]。目前GMM在致动器、换能器和传感器等领域已经得到了广泛应用，为超磁致伸缩能量收集相关研究奠定了一定的理论基础[4-6]。振动能量收集是指利用特定能量的技术，对于缓解能源压力以及提升能源的利用率具有一定意义[7-9]。超磁致伸缩式能量收集装置(Giant magnetostrictive energy harvesting device，GMEHD)基于GMM的维拉里效应，将外界的机械振动能转换为可储存使用的电能，具有输出功率高、工作稳定性强、应用适应性广等优势，可为微机电系统甚至是常用的中小型功率器件供电，具有较好的发展潜力[10-13]。从20世纪80年代开始，国外研究机构尝试采集振动能量，并且论证了振动能量回收应用于微功耗器件驱动的可行性。

目前，针对超磁致伸缩致动器的研究很全面，体系也已经很成熟，但对能量收集方面研究并不多。国内外学者致力于研究实用性更强的应用型新结构，然而对材料非线性、机电耦合特性等考虑较少，现有模型的研究大多集中于GMM棒磁化模型，并未遵循能量收集的相关工作过程；对GMEHD的有限元仿真分析也十分有限，部分仿真的假设过于简单，与材料本征不够吻合，仿真结论不可靠。本文根据机械振动通常具有周期性往复的实际特点，设计一种柱棒式GMEHD，理论上棒式GMEHD进行能量回收可采集任意频率下的振动能，而且其对体积要求低，可做成闭合磁路、避免磁泄漏，有效提高材料的机电转换效率；并且，棒式能量回收结构与磁致伸缩棒式致动器结构几乎一样，材料的磁机耦合特性也完全相同，由于致动器研究的成熟，该类型结构具有较好的研究基础[14]。为准确计算能量收集产生的电动势，结合其实际工作过程，建立系统的输入输出模型，并通过有限元仿真分析以及实验研究对模型准确性进行验证及对比分析，以期为GMEHD结构优化和实际应用奠定基础。

1 基本结构与原理

1.1 基本结构

设计了图1所示的柱棒式GMEHD，核心元件为GMM棒；永磁体作为偏置磁铁为GMM棒提供偏置磁场，能够使GMEHD工作于机电耦合系数较高的线性区间[15-16]，同时将偏置磁铁上下对置，相对周向放置减小了一定体积；由于GMM棒抗拉强度低，脆性较大，同时为了便于GMEHD接受外界激励，在实际应用中需要设计承力杆[17]；预紧弹簧为GMM棒提供预压力，通过调整盖帽和套筒之间的螺纹可调整预紧力；盖帽、套筒和支座均采用高导磁材料，整个装置构成闭合磁路，实现输出效率最大化。

图1 能量收集装置结构图Fig.1 Structure diagram of energy harvesting device1.承力杆 2.预紧弹簧 3.偏置磁铁 4.采集线圈 5.力传感器预留位置 6.底部引线槽 7.固定螺栓孔 8.支座 9.超磁致伸缩棒 10.侧方引线槽 11.套筒 12.盖帽

1.2 工作原理

在机械应力作用下材料产生应变，会引起GMM棒内部磁化状态发生变化，这种现象称为磁致伸缩逆效应，又称维拉里效应。

根据维拉里效应，如图2所示，GMM棒一端固定，一端受力，外界压力通过承力杆和预紧弹簧作用到GMM棒上。GMM棒形状发生变化，其纵向长度减小使其内部磁畴会发生偏转，从而使GMM棒的内部磁场分布发生改变，其磁通量发生了变化。由法拉第电磁感应定律，如果GMM棒外部绕有感应线圈，就会产生感应电动势并可通过线圈进行收集[18-19]。

图2 GMEHD工作原理图Fig.2 Working principles of GMEHD

2 系统建模

能量收集是将机械能转换为磁场能最终转换为电势能的过程，故模型需建立输入力和输出电动势之间的关系。相较于大多数现有模型不同，本模型充分考虑了能量收集工作整个过程，从GMEHD受到外界激励到GMM棒产生形变，再到GMM棒内部产生变化的磁场，最后通过线圈产生感应电动势，模型更贴近装置的实际工作过程。建模过程如图3所示。

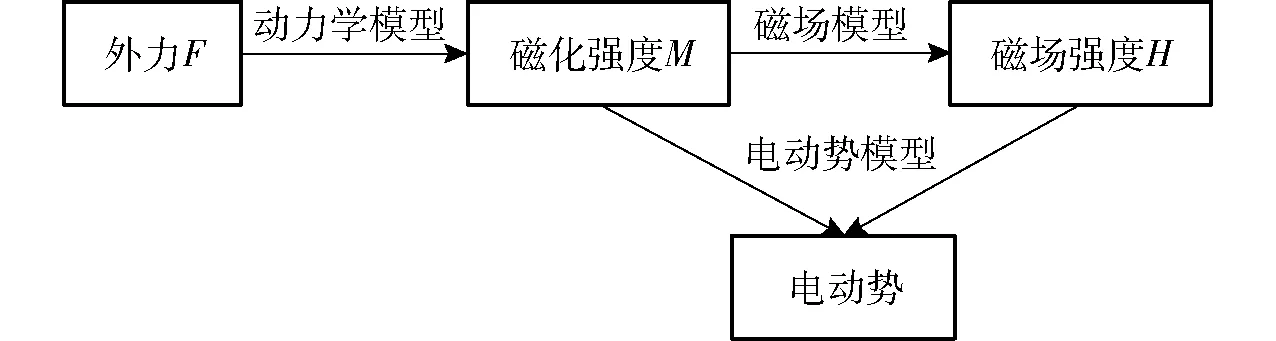
图3 GMEHD建模流程图Fig.3 Flow chart of GMEHD modeling

GMM棒在偏置磁场作用下的振动过程和磁化情况比较复杂，所以对装置进行建模时作如下假设：①GMM棒的横截面在振动时始终保持为平面作整体运动，并略去其纵向伸缩引起的横向变形。②GMM棒受到的应力σ、产生的压应变ε、偏置磁场强度H0和产生的磁场强度H均匀分布。③将GMM棒等效为质量-弹簧-阻尼模型，并假设其等效阻尼系数c和弹性模量E不随外界力的变化而改变。④忽略预紧弹簧对系统输入力的影响，GMM棒能够完全得到外界力的输入。

2.1 动力学模型

基于上述假设，将GMEHD简化为单自由度振动系统，如图4所示。

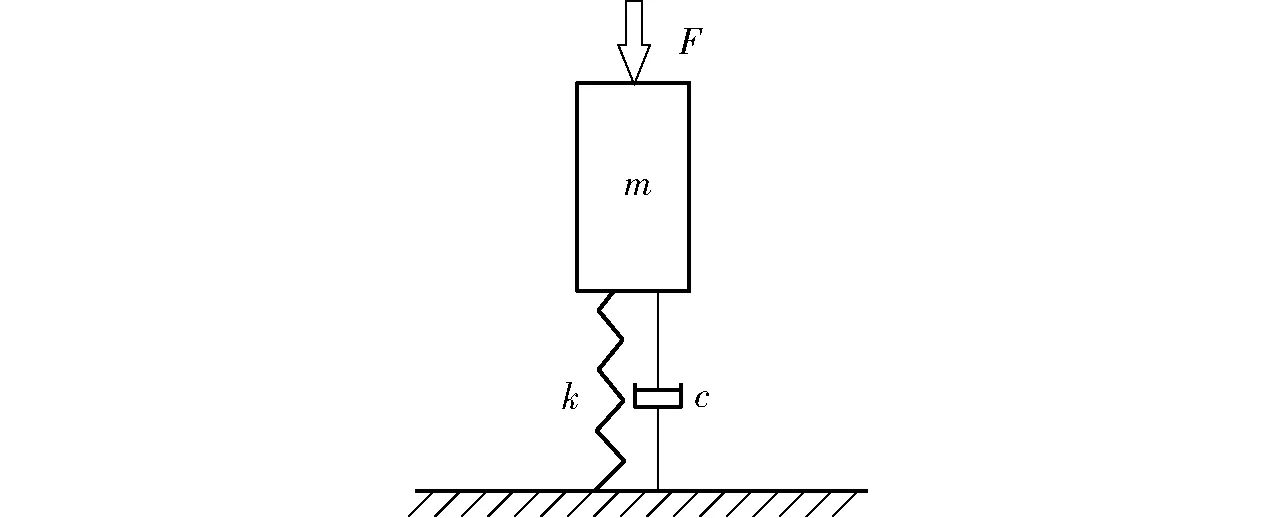
图4 GMEHD等效模型Fig.4 GMEHD equivalent model

取GMM棒中心平衡点为坐标原点，x轴正方向竖直向下，由图4的二阶线性有阻尼质量-弹簧系统，得到系统的动力学微分方程

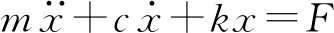
(1)

式中m——GMM棒等效质量

k——GMM棒等效刚度

x——GMM棒位移

由GMM棒的位移可得到其应变为

(2)

式中l——GMM棒长度

当对GMM棒施加压应力时，其磁畴将主要沿垂直轴线的易磁化方向分布。此时，GMM棒的应变λ与磁化强度M的关系近似为基于能量基础的二次畴转模型

(3)

式中λs——GMM棒的饱和磁致伸缩应变

Ms——GMM棒的饱和磁化强度

2.2 磁场模型

在外力作用下，GMM产生伸缩应变，进而导致其内部有效磁场发生变化。由热动力学基本定理可得棒内的Helmholtz自由能密度为

(4)

式中μ0——真空磁导率

H0——偏置磁场强度

α——畴壁相互作用系数

σ——GMM棒在外力作用下的应力

T——内部温度S——熵

Helmholtz自由能密度J关于磁化强度M的微分即为有效磁场，式(4)对M微分，得

(5)

式(3)两边对M微分，得

(6)

将式(6)代入式(5)中，得

(7)

(8)

式中A——横截面积

2.3 电动势模型

考虑GMM固有的磁滞非线性，由电磁学原理可得棒内磁感应强度为

B=μ0(M+H)

(9)

在得到GMM棒内磁感应强度B后，由法拉第电磁感应定律可计算产生的感应电动势为

(10)

式中Φ——GMM棒内部的磁通量

n——线圈匝数

将式(9)代入式(10)，可得

(11)

将式(3)、(8)代入式(11)，得

(12)

将式(2)代入式(12)，得

(13)

联立式(1)、(13)即可得到在一定输入力作用下GMEHD所产生的电动势。

2.4 模型求解

在外界环境中，振动往往具有周期性或阶段周期性，通过傅里叶变换，可将非正弦的周期性外力分解为一系列周期性正弦力的线性组合，因此以正弦力为输入，借助式(1)、(13)，计算系统的输出电动势。

为了确保正弦力在不同时刻均能够完全作用到GMEHD上，即为了使正弦力始终为正，预应力应大于或等于正弦力的幅值。在预应力和正弦力的共同作用下，令外力F=F0+F1sin(ωt)，则式(1)为

(14)

式中F0——预应力

F1——正弦力幅值

ω——正弦力频率

由振动理论可知，单自由度强迫振动微分方程的全部解包括稳态振动与瞬态振动。稳态振动是外界激励下的强迫振动，在正弦激励下为持续等幅振动，瞬态振动在阻尼情况下为衰减振动，只在振动开始后的一段时间才有意义，一般情况下可以不考虑。分开讨论稳态振动预应力和正弦力。

预应力F0为施加在GMM棒上的静力，其产生的位移x1为静位移，不会有速度和加速度的产生，所以x1为

(15)

正弦力F1sin(ωt)为施加在GMM棒上的简谐力，由单自由度强迫振动对简谐激励的响应结果可以得到动位移x2为

x2=Xsin(ωt-θ)

(16)

(17)

(18)

故GMM棒的总位移x为

(19)

将式(19)代入式(13)中，得到GMEHD在正弦力下的输出电动势为

(20)

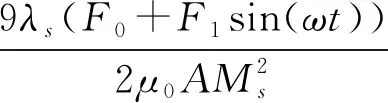
(21)

通过式(21)可以看出，在一定预应力和正弦力共同作用下，GMEHD的输出电动势幅值和输入正弦力的频率呈线性关系；在外力及GMEHD一定的情况下，除了简谐量外均为常数，其中正弦量不影响输出电动势u的相位，其相位与输入正弦力相比，超前π/2。

2.5 线圈优化

2.5.1线圈结构

GMEHD采用多层绕组圆柱形线圈，其结构如图5所示。线圈骨架为空心圆筒，r1为内径，r2为外径，h为骨架高度，铜漆包线由铜芯构成，半径为r，绕组高度为D(即r2-r1)。

图5 多层圆柱形线圈示意图Fig.5 Schematic of multilayered cylindrical coil

结合多层绕组圆柱形线圈的结构以及电阻公式，每一匝线圈的平均长度为π(r1+r2)，则整个线圈的电阻R为

(22)

式中ρ——铜芯电阻率

在线圈骨架结构一定的情况下，线圈匝数N与铜芯半径r会受到结构尺寸的约束，即

(23)

在线圈的实际缠绕过程中，不可避免会在漆包线之间产生间隔，实际的线圈匝数达不到理想计算结果，所以对式(23)添加修正系数η(0<η<1)，即

(24)

消去r，得

(25)

在线圈骨架一定的情况下，r1、r2、D、h均为定值，同时在铜漆包线材质一定的情况下，电阻率ρ也为定值，因此线圈电阻R与匝数平方成正比，令

(26)

则

R=C1n2

(27)

在线圈高h大于绕组高度D时，内含磁心的多层绕组圆柱形线圈的电感L为[20]

(28)

式中μr——GMM棒相对磁导率

W——(r1+r2)/h的函数

V——h/D的函数

在线圈骨架一定的情况下，这三者均可视为常数，因此线圈自感L与匝数平方成正比，令

(29)

则

L=C2n2

(30)

2.5.2电路分析

图6 线圈等效电路Fig.6 Coil equivalent circuit

由于GMEHD产生交流电动势，在分析线圈对输出电动势的影响时，除了考虑线圈的直流阻抗外，还需考虑其感抗对输出电动势的影响。图6是线圈的等效电路。其中，u是GMEHD产生的交流电动势，i为电路中的电流，R2为外接负载电阻，u2为负载电阻上的电压。将线圈等效为电阻R和电感L的串联，u1为线圈上的电压，ur、uL分别是电阻R和电感L上的电压。为简化求解过程，对电路进行分析时采用相量图作为辅助分析工具，根据相量图的几何关系便可对电路进行相关运算。得到图6的相量图如图7所示。

图7 电路相量图Fig.7 Phasor diagram of circuit

以I为参考相量，外接负载电阻R两端电压U2与I同相，线圈上的电压U1含有两个分量：电阻r上的电压Ur也与I同相；电感L上的电压UL较I超前90°。由相量图得(U2，U1，U)和(Ur，UL，U1)2个电压三角形，由相量图应用余弦定理计算

(31)

其中

XL=ωL=2πfL

(32)

式中φ——线圈电路相位角

XL——线圈感抗

由式(27)、(30)～(32)可以解得

(33)

从式(33)可以看出，φ不受线圈匝数n的影响。由式(21)可知，在外界输入力一定以及GMM棒结构参数确定的情况下，GMEHD产生的电动势与匝数n呈线性关系

U=c1n

(34)

式中c1——比例常数

则整个电路的有功功率P为

(35)

在外接负载电阻R2一定时，P只与线圈匝数n相关，将式(35)变形得

(36)

(37)

2.5.3线圈匝数

根据GMEHD以及使用的GMM棒的结构尺寸，确定线圈各参数如表1所示。

表1 线圈各参数Tab.1 Parameter in coil

线圈各项参数确定后，即可确定出W与V取值为5与0.87。由式(37)可知，除了线圈结构参数与外接电阻之外，输入力频率f也会影响线圈匝数。图8是匝数n与输入力频率f的关系曲线。

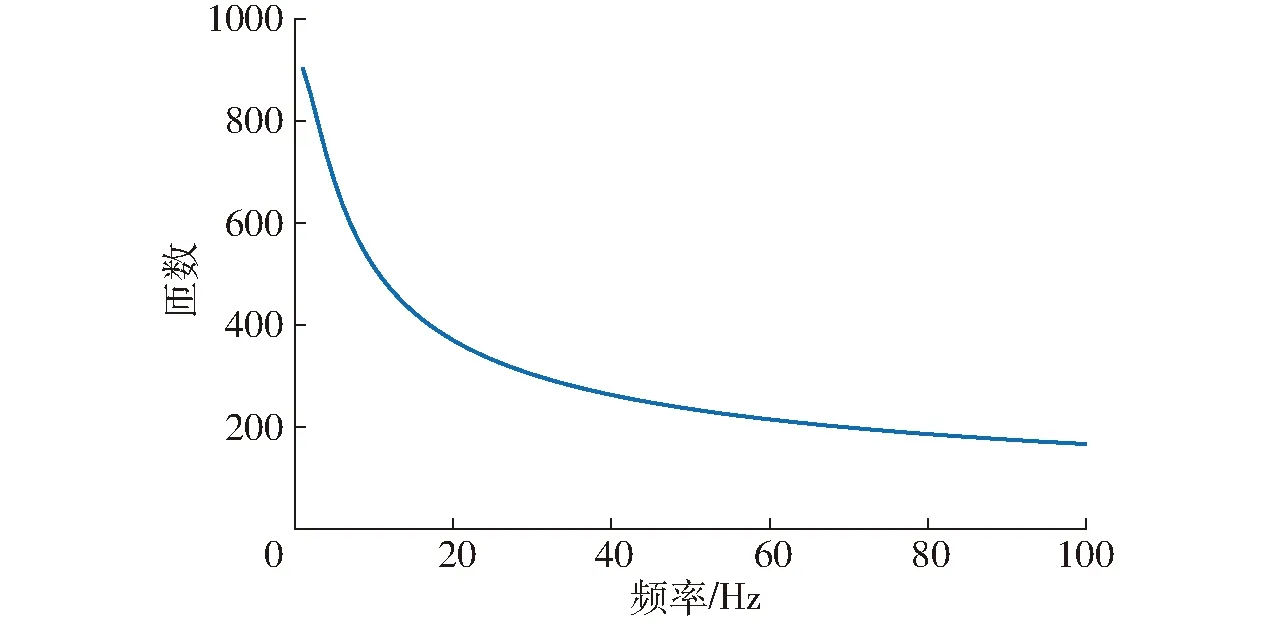
图8 线圈匝数与输入力频率的关系曲线Fig.8 Relationship curve of coil turns and input force frequency

3 仿真

利用有限元软件COMSOL Multiphysics建立有限元模型，设置模型相关组件，对GMEHD进行仿真分析。

3.1 有限元模型

图9 几何模型Fig.9 Geometric model

建立GMEHD几何模型，如图9所示。由于GMEHD为轴对称结构，无需建立GMEHD的实际三维空间结构，仅建立了GMEHD的二维平面模型，在保证不影响计算结果精度的情况下，简化了模型，减小了计算量。

3.2 模型参数设置

对几何模型各部分添加不同的材料，材料参数如表2所示。

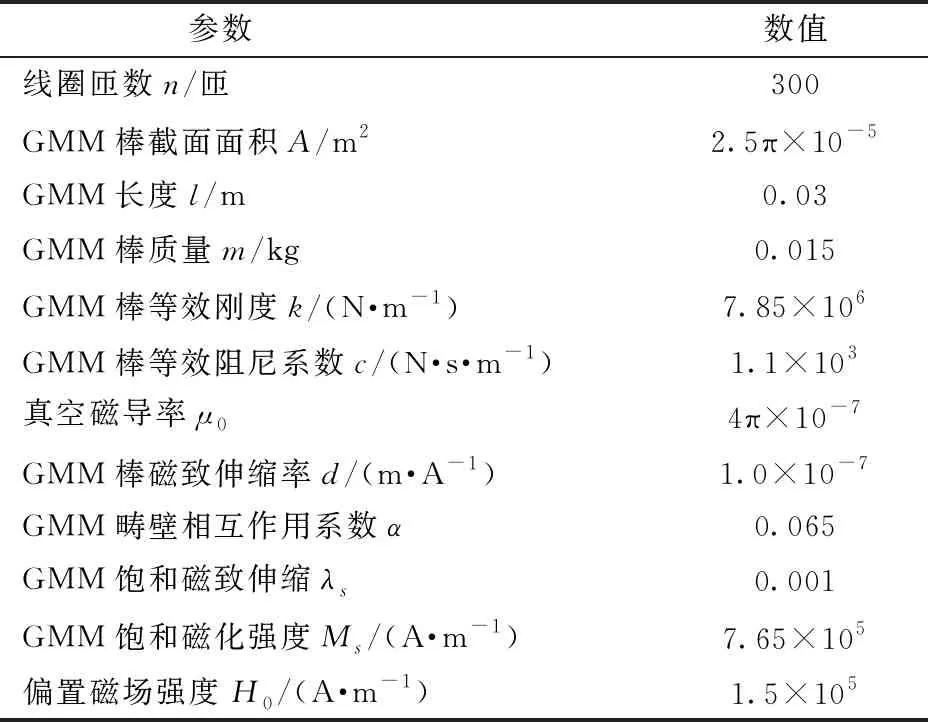
表2 有限元模型各参数Tab.2 Parameter in finite element model

物理场选择包含固体力学场和磁场的耦合场，在GMEHD底端设置固定约束，顶杆上端设置预应力以及相应载荷。网格剖分选择由用户控制网格，对不同区域选择不同网格形状和大小，在保证精度的情况下减小计算量，网格剖分结果如图10所示。在完成相关设置后进行计算，即可得到仿真分析的结果。

3.3 仿真结果

将1 N预应力以及幅值1 N、频率1 Hz的正弦力共同作用到承力杆上，可得GMEHD的磁感应强度分布图，图11为一个正弦周期内不同时间节点的磁感应强度分布图。

图10 网格剖分图Fig.10 Mesh split diagram

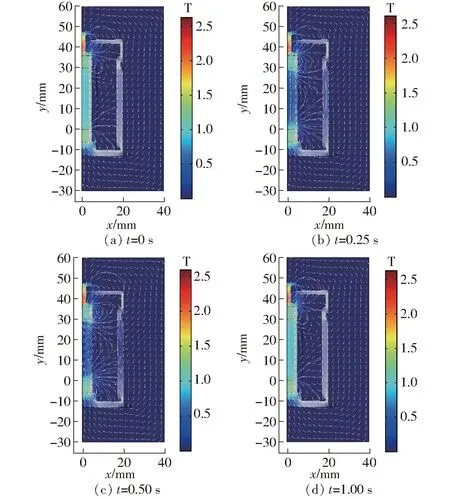
图11 磁感应强度分布图Fig.11 Magnetic induction distribution diagrams

通过图11可以看出，随着时间的变化，在GMEHD中磁感应强度变化率最大的是GMM棒，基于此可通过GMM的逆磁效应得到感生电动势。

4 实验

为验证模型的有效性，制作了GMEHD样机(力传感器在试验时置于GMEHD内部)，GMM棒采用定向凝固法制备，输出杆、端盖、外壳和底座均采用高磁导率的15号低碳钢，各结构参数均与有限元仿真设定值一致，样机实物如图12所示。

图12 GMEHD和力传感器Fig.12 GMEHD and force sensor

4.1 实验系统

图13 实验系统Fig.13 Experiment system1.函数信号发生器 2.模态激振器 3.固定支架 4.电荷放大器 5.数据采集器 6.功率放大器 7.计算机

用于测试GMEHD输出电动势实验系统如图13所示。实验过程为：DC1022U型函数信号发生器产生输入信号，信号经PA020型功率放大器放大后输入到JZ020型模态激振器中，模态激振器通过输出顶杆将力传递到GMEHD，GMM棒受到外力后产生电动势；将GMEHD中力传感器测得的输入力信号经PE01AD型电荷放大器后接入到SA1604型数据采集器中的一个通道中，同时将GMEHD产生的电动势接入到数据采集器的另一通道中，再将数据采集器接入到计算机中，计算机端便可通过数据采集器的配套软件进行实验测量与数据记录。

4.2 实验测量

由于GMM材料抗压不抗拉，同时为了使GMM棒在正弦力输入下能够不出现伸长的情况，在实验前通过调整盖帽和套筒之间的螺纹给予GMEHD一定的预压力，保证GMM棒工作在合适的变形范围内，并防止其受到拉应力而发生断裂。在实验中以不同频率单位正弦力为激励，通过置于GMM棒下的力传感器及数据采集器，可以得到输入力-时间曲线，如图14所示。

图14 不同输入力频率的力幅值曲线Fig.14 Time curves of different frequency input force

将线圈得到的电动势信号接入到数据采集器的另一通道中，可得到在不同频率正弦力下的电动势随时间变化的曲线，如图15所示。

图15 不同输入力频率下的输出电动势曲线Fig.15 Output electromotive force curves under different frequency forces

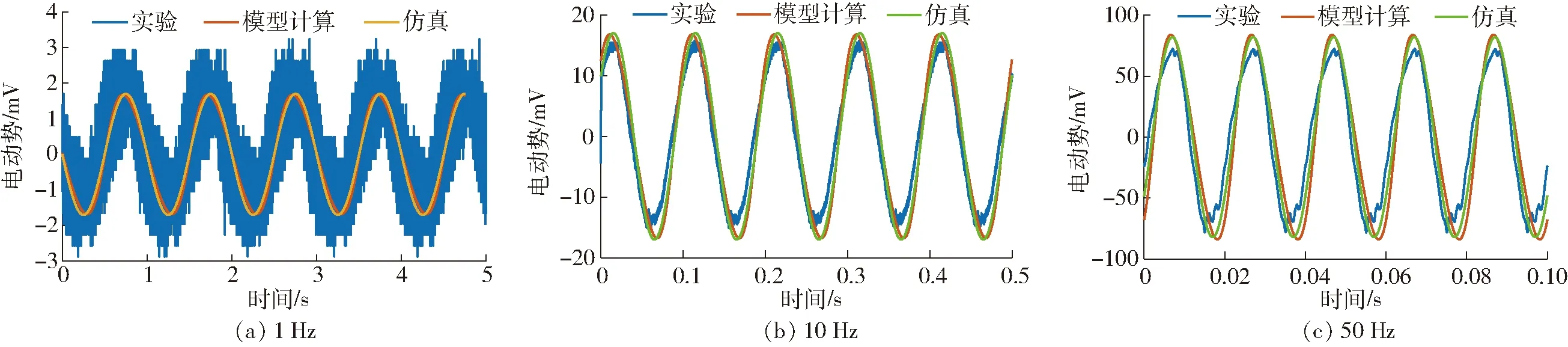
图17 不同输入力频率下的输出电动势曲线对比Fig.17 Comparison of output electromotive force curves under different frequency forces

由图15可知，在输入正弦力频率只有1 Hz时，电动势幅值在2 mV左右，因幅值较小，所以受振动干扰影响较大，输出波形噪声较大，但仍能够看出波形形状；当频率达到10 Hz时，输出波形较为稳定且清晰，电动势幅值在15 mV左右；当频率达到50 Hz时，电动势幅值能够达到75 mV，输出电动势幅值与输入正弦力频率基本呈线性关系；图16是输入力10 Hz时与输出电动势的对比，可以看出输入力频率不影响GMEHD输出电动势的相位，其始终超前于输入力相位π/2，原因是线圈为电感元件，而在电感元件电路中，在相位上电流始终比电压滞后π/2，且电流与磁场强度、输入力的相位一致，会使得输出电动势相位超前输入力π/2。这均与理论分析结果一致。

图16 10 Hz时输入正弦力与输出电动势对比Fig.16 Comparison of input sinusoidal force and output electromotive force at 10 Hz

4.3 对比分析

将实验所得电动势曲线分别与模型计算值和有限元仿真结果进行对比，如图17所示。由图17可以看出，在频率为1 Hz时因受振动噪声影响较大，造成实验结果比模型计算值和仿真结果大，在频率为10、50 Hz时，实验结果比模型计算值和仿真结果略小，因为在模型计算和有限元仿真分析时，没有考虑从GMEHD输入顶杆到GMM棒这一碰撞过程中的输入力能量损耗，而在实验时这一损耗实际存在，从而在一定程度上影响输出电动势的幅值，造成实验结果比模型计算值和有限元仿真结果略小。以输入力频率10 Hz时为例，模型计算与仿真得到的输出电动势幅值为17 mV，实验所得输出电动势幅值为15 mV，相对误差为11.7%，由于碰撞损耗不可避免，误差在合理范围之内，不影响实验对模型准确性的验证。