基于微分几何与EDEM的船型开畦沟装置触土曲面优化

刘晓鹏 张青松 刘立超 魏国粱 肖文立 廖庆喜

(1.武汉轻工大学动物科学与营养工程学院， 武汉 430023; 2.武汉轻工大学湖北省粮油机械工程技术研究中心， 武汉 430023; 3.华中农业大学工学院， 武汉 430070； 4.农业农村部长江中下游农业装备重点实验室， 武汉 430070)

0 引言

油菜是我国重要油料作物，长江中下游地区是我国冬油菜主要种植区域，该地区土壤黏重、板结，且春、秋两季雨水充沛，油菜易遭受渍害[1]，油菜播种作业时需同步在种床厢面两侧开用于排水的畦沟。机械化开畦沟作业多采用被动式犁体或主动式开沟机具[2-3]。相比主动式开沟机具，被动式犁体结构更简单，能适应较高的作业速度，在农田开沟领域得到了广泛应用。

犁体曲面是一种复杂的空间曲面，常用的犁体多采用水平直元线原理形成犁体曲面[4-5]。犁体曲面的结构参数、形状变化是影响其作业效果和牵引阻力的重要因素[6-7]。国内外学者在犁体曲面设计和减阻特性方面开展了诸多研究[8-13]。犁体曲面结构复杂，通过高速数字化土槽或田间试验的手段研究曲面性质难度较大。近些年来，基于离散元和有限元理论的现代设计方法广泛应用于犁体曲面的研究中[14-17]，但这些研究主要针对犁体曲面阻力与宏观结构参数之间关系进行分析，由于犁体曲面形状变化难以量化描述，鲜有针对犁体曲面形状变化对牵引阻力影响的研究，犁体曲面的减阻设计缺乏相关方法和理论依据。

微分几何是运用微积分理论研究空间曲线、曲面形状变化等几何性质的学科，在机械工程领域得到广泛应用[18-21]。华中农业大学工学院研制的驱动圆盘犁对置组合式耕整机采用组合式船型开畦沟装置进行开畦沟，其中，开畦沟前犁、船式开沟犁为开畦沟装置的主要触土部件。本文以开畦沟前犁、船式开沟犁为研究对象，采用微分几何理论结合离散元仿真方法，建立能量化描述犁体曲面形状变化的微分几何表达式，分析犁体曲面形状变化、结构参数对牵引阻力的影响，寻求适用于组合式船型开畦沟装置触土部件低耗、减阻设计的理论依据，以获得具有较优减阻特性的犁体曲面形式。

1 开畦沟装置结构与工作原理

图1 驱动圆盘犁对置组合式耕整机结构示意图Fig.1 Structural sketches of symmetrical driven disc plows combined tillage machine1.碎土辊 2调节装置 3.限深轮 4.船式开沟犁 5.侧边齿轮箱 6.驱动圆盘犁组 7.万向节 8.中央齿轮箱 9.主机架 10.开畦沟前犁 11.三点悬挂装置

驱动圆盘犁对置组合式耕整机主要由主机架、中央齿轮箱、侧边齿轮箱、驱动圆盘犁组、组合式船型开畦沟装置、限深轮、碎土辊等组成，如图1a所示，其结构与工作原理见文献[22-23]。其中，组合式船型开畦沟装置由开畦沟前犁、船式开沟犁组成。

作业时，开畦沟前犁破土形成初步沟型，船式开沟犁分土曲面将前犁开沟后残留土壤分向两侧，犁体整形曲面侧向挤压土壤形成满足油菜播种开畦沟农艺要求的梯形畦沟。其中，开畦沟前犁犁体曲面、船式开沟犁整形曲面为开畦沟装置工作时的主要触土、受载曲面。

2 开畦沟装置主要触土曲面设计与分析

根据开畦沟装置的工作原理可知，开畦沟前犁、船式开沟犁的主要触土曲面分别为结构对称的前犁犁体曲面和整形曲面(如图1b、1c)。二者均采用水平直元线法设计，直元线QQ′沿导曲线AB按元线角(θ或Φ)均匀减小变化形成，如图2所示。

图2 开畦沟装置主要触土曲面Fig.2 Soil contact surfaces of ditching furrow system

2.1 开畦沟装置牵引阻力分析

整机作业时，对置驱动圆盘犁组分别向机组外侧翻耕土壤，在中间未耕区域形成如图3所示的凸起开畦沟区域及犁沟，其中，犁沟沟壁由内侧圆盘犁耕后形成。组合式船型开畦沟装置将开畦沟区域土壤侧向挤压，填埋犁沟并形成完整畦沟。开畦沟装置受到的牵引阻力主要由对称布置的前犁犁体曲面、整形曲面与土壤作用产生，如图3a所示。开畦沟装置所受牵引阻力Fd为

Fd=F1+F2

(1)

式中F1——开畦沟前犁牵引阻力，N

F2——船式开沟犁牵引阻力，N

图3 开畦沟装置主要触土曲面工作原理图Fig.3 Soil contact surfaces of ditching furrow system

触土曲面的结构参数、形状变化是影响犁体牵引阻力的主要因素[6-7]。由图2可知，触土曲面主要结构参数为最大元线角、最小元线角(元线角最大变化量)、高度、宽度、导曲线长度、开度。当结构参数一定时，曲面形状变化则由导曲线类型决定。若设前犁犁体曲面、整形曲面扰动单位体积土壤产生的牵引阻力分别为f1和f2，则

(2)

式中θmax——前犁犁体曲面最大元线角，(°)

θmin——前犁犁体曲面最小元线角，(°)

w——前犁犁体曲面宽度，mm

h——前犁犁体曲面高度，mm

l——前犁犁体导曲线开度，mm

V1——开畦沟前犁扰动土壤体积，mm3

Φmax——整形曲面最大元线角，(°)

Φmin——整形曲面最小元线角，(°)

Lz——整形曲面导曲线长度，mm

Hq——整形曲面高度，mm

V2——船式开沟犁扰动土壤体积，mm3

T——导曲线类型

Ha——开沟深度，mm

Ls——作业距离，mm

Lq——开畦沟区域宽度，mm

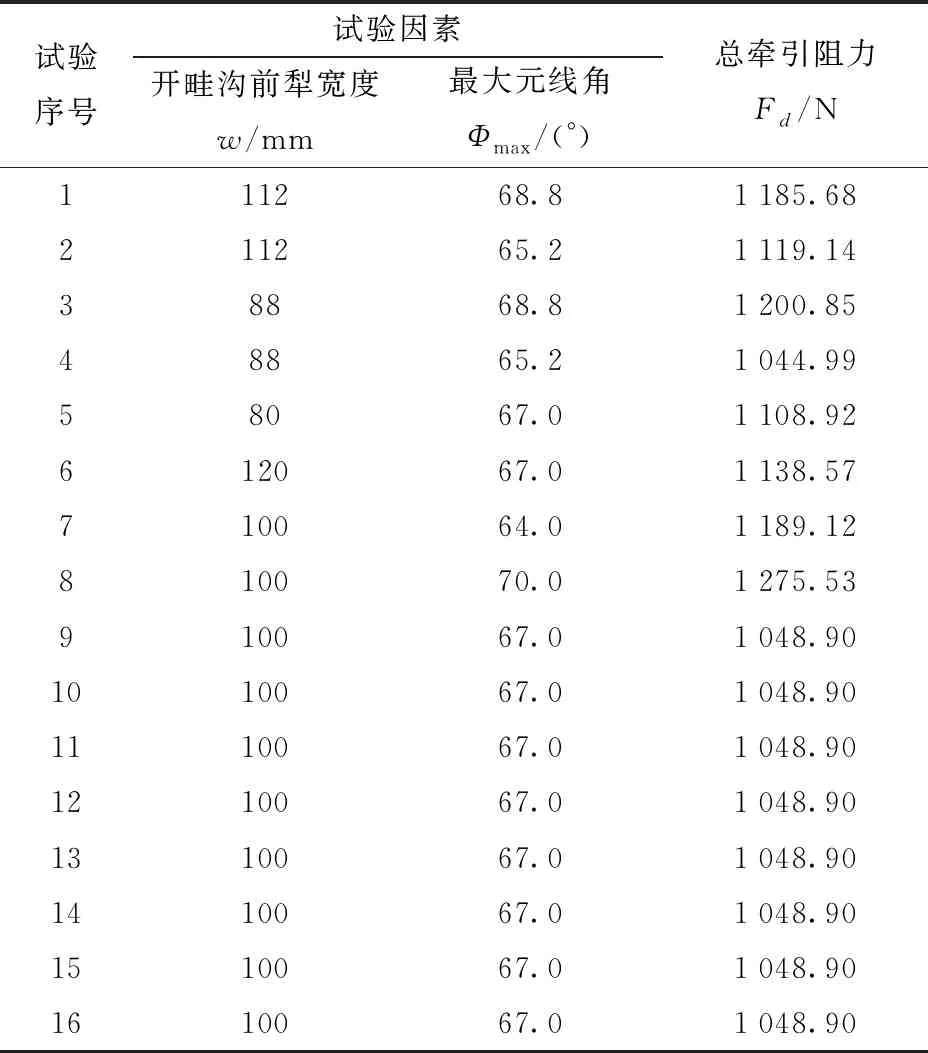
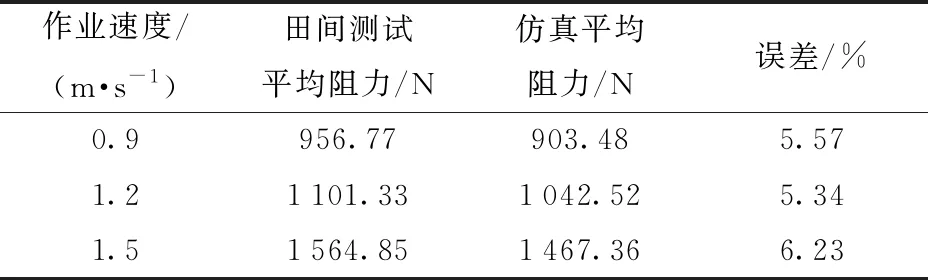
由式(1)、(2)可知，除决定触土曲面形状变化的导曲线类型T外，当开畦沟区域宽度Lq一定时，前犁宽度w直接决定了开畦沟前犁与船式开沟犁作业时的扰动土壤体积V1和V2。由于两种犁体工作原理不同，船式开沟犁挤压土壤体积相对较大，故f1

2.2 开畦沟前犁犁体曲面参数设计与分析

根据油菜播种开畦沟农艺要求，设计开畦沟装置拟开出沟深250～300 mm、沟宽300～400 mm、沟底宽120 mm的梯形畦沟。由于后置的船式开沟犁在前犁开出初步沟型上形成梯形畦沟，故前犁犁体宽度应不大于最终畦沟沟底宽。根据开畦沟装置牵引阻力分析可知，前犁犁体曲面宽度w过大或过小均会影响开畦沟质量，故取w为80～120 mm。开畦沟前犁犁体曲面高度h应略高于实际开沟深度，设计取h=350 mm。参考文献[4]水平直元线犁体设计方法，为保证前犁入土能力，设计犁体最小元线角θmin为40°。元线角最大变化量Δθmax为5°，即θmax为45°。由图2a可知，前犁犁体曲面导曲线长度即为犁体高度h，则

(3)

式中lCC′——犁体外侧开度，mm

λ——开畦沟前犁导曲线高宽比

开畦沟前犁作用主要为破土，由图2a中几何关系可知，其导曲线为切削刃口曲线，导曲线末端B点处切线与水平面夹角δ为入土角，导曲线类型决定了曲面形状变化，故导曲线高宽比λ和导曲线类型为影响犁体破土性能主要因素。当导曲线类型一定时，若导曲线高宽比λ过小，则犁体入土角δ较小而不利于入土；若导曲线高宽比λ过大，则切削刃口(导曲线)过于平滑致使犁体破土能力较差。为保证前犁破土性能，设计取犁体外侧开度lCC′为50 mm。由式(3)可得导曲线开度l为58～62 mm，导曲线高宽比λ≈6。此时犁体切削刃口合理平滑变化，能保证犁体破土性能。

2.3 船式开沟犁整形曲面参数设计与分析

假设开畦沟前犁开沟扰动的土壤均匀堆积于沟壁两侧地表(图3b)，为保证船式开沟犁整形曲面能充分对开畦沟前犁扰动后的土壤作用，应满足

(4)

式中ha——开畦沟前犁扰动土壤两侧堆积高度，mm

S1——开畦沟前犁单侧扰动土壤面积，mm2

船式开沟犁侧向挤压土壤模型见文献[23]，参阅文献[23]设计中间开畦沟区域宽度Lq为350 mm，能有效保证侧向挤压土壤填埋驱动圆盘犁形成的犁沟。由式(4)可得Hq≥380 mm。因此，设计选取船式开沟犁整形曲面高度Hq为380 mm。由船式开沟犁的工作原理(图3b)可知，其犁体梯形截面宽度wq即为最终开出畦沟沟底宽，故取wq为120 mm。整形曲面长度即为导曲线长度Lz，若长度Lz过小，则犁体会因扰土体积小而难以有效侧向挤压土壤填埋犁沟。若长度Lz过大，则犁体触土面积过大而增加犁体磨损。考虑整形曲面触土面积应适中，设计选取整形曲面长度(导曲线长度)Lz为300 mm。

当导曲线类型T、长度Lz一定时，根据文献[22]对船式开沟犁整形曲面挤压过程进行分析，为使整形曲面具有较好侧向挤压能力，应满足

Φmax≤90°-φ

(5)

式中φ——土壤摩擦角，取20°～26°[4]

由式(5)可得Φmax≤70°。整形曲面前端开度Sq和导曲线开度lq由最大元线角Φmax、最小元线角Φmin决定，由图3b几何关系得

(6)

式中Sq——整形曲面前端开度，mm

ΔΦmax——元线角最大变化量，(°)

λq——整形曲面导曲线高宽比

由式(5)、(6)可知，若最大元线角Φmax较小，会增大整形曲面前端开度Sq，使船式开沟犁前端分土曲面承受较大阻力。故最大元线角Φmax不宜取较小值，设计选取Φmax为64°～70°，可满足整形曲面具有较好挤压能力的同时降低阻力。本文设计取元线角最大变化量ΔΦmax为5°，即最小元线角Φmin为59°～65°。此时导曲线开度为98～103 mm，导曲线高宽比λq≈3，处于较合理范围，导曲线能平滑变化并同时保证犁体侧向挤压能力。

2.4 主要触土曲面微分几何性质分析

由前文分析可知，当犁体曲面结构参数一定时，曲面的导曲线类型T不同，会使犁体曲面形状变化出现差异，影响犁体牵引阻力。由于传统解析几何方法难以量化描述犁体曲面的形状变化，本文采用微分几何方法，通过建立曲面参数方程并进行若干次微商，构造适当的代数表达式(内蕴几何量)以量化描述不同导曲线类型的犁体曲面形状变化。

2.4.1参数方程建立

前犁犁体曲面和整形曲面均可看作为直纹面，分别建立如图2所示坐标系，根据曲面解析几何理论[18]，两种犁体曲面均参数方程可表示为

r(κ,τ)=lQQ+τlQQ′

(7)

式中κ——变量参数

τ——常数变量，0≤τ≤1

由图2中几何关系可得，前犁犁体曲面和整形曲面参数方程均可表示为

r(κ,τ)=
(τF(κ)+(1-τ)(l(κ)+lκ),L(κ),(1-τ)Hκ)

(8)

式中lκ——导曲线前端开度，mm

Hκ——导曲线长度，mm

l(κ)——导曲线开度关于变量参数κ的函数

L(κ)——导曲线长度关于变量参数κ的函数

F(κ)——犁体外侧开度lCC′关于变量参数κ的函数

为便于计算和表达前犁犁体曲面、整形曲面的几何特性，分别选取元线角变化量κ=Δθ=θmax-θ或κ=ΔΦ=Φmax-Φ、常数变量τ作为方程的变量参数。对于前犁犁体曲面，lκ、Hκ取值分别为wcotθmax/2和(1-τ)w/2。对于整形曲面，lκ、Hκ取值分别为HqcotΦmax和Hq。当导曲线类型不同时，变量参数Δθ、ΔΦ的变化率出现差异，则参数方程的表达形式会出现较大差异。

2.4.2不同导曲线型触土曲面形状变化分析

微分几何的曲面理论中，空间曲面的形状变化可由如下两个微分方程来表达[18]

(9)

式中Σ1——曲面第1基本形式

Σ2——曲面第2基本形式

E、F、G——第1类内蕴几何量

L、M、N——第2类内蕴几何量

其中，内蕴几何量E、F、G、L、M、N按文献[18]

中方法计算

(10)

由式(9)可知，当变量参数κ、τ确定时，内蕴几何量E、F、G、L、M、N决定了上述微分方程的表达形式。因此，通过计算曲面的内蕴几何量，可以量化描述曲面的形状变化。由于犁体曲面导曲线常设计为直线、抛物线、指数曲线形式[4]，故本文选取上述3种导曲线类型的前犁犁体曲面、整形曲面为研究对象，分别按式(10)计算对应曲面的内蕴几何量，以量化描述不同导曲线类型犁体主要触土曲面的形状变化差异。根据水平直元线形成原理，曲面形状均匀变化可使曲面具有更好力学特性[4-5]。因此，由式(7)可知，曲面变量参数κ随着导曲线开度和犁体底面开度均匀变化，此时函数l(κ)、F(κ)可视为一次线性函数。变量参数κ随导曲线长度变化的函数L(κ)形式应与导曲线形式相同。则3种导曲线类型犁体参数方程中的各函数可设为如表1所示的形式。

表1 参数方程函数表达形式Tab.1 Expressions of functions in parametric equations

将上述函数代入式(7)、(10)中计算结果如表2所示，3种导曲线类型的触土曲面对应的内蕴几何量F、G、N均相同，故内蕴几何量E、L、M是体现本文研究触土曲面形状变化差异的主要因素。由表2中内蕴几何量E、L、M表达式可知，当曲面导曲线类型一定时，随着曲面结构参数的变化，内蕴几何量E、L、M仍具有相同的表达形式，即结构参数变化不会影响内蕴几何量的变化趋势。当曲面结构参数一定时，曲面形状变化(导曲线类型变化)主要体现在内蕴几何量E、L、M变化趋势的不同，影响触土曲面牵引阻力。

表2 不同导曲线类型曲面内蕴几何量Tab.2 Calculated results for intrinsic geometrical quantity of surface with different guide curves

3 EDEM仿真

3.1 模型建立

3.1.1本征参数与接触模型

长江中下游地区常年稻油轮作，该区域为粘质土壤，参阅文献[24-25]及田间实地测量，本文选用半径为8 mm的球形颗粒模拟田间土壤，土壤泊松比为0.38、剪切模量为1×106Pa、密度为1 850 kg/m3。开畦沟部件材料设置为钢材，泊松比为0.3、剪切模量为7.9×1010Pa、密度为7 860 kg/m3。土壤-土壤和土壤-犁体恢复系数均为0.6、土壤-土壤和土壤-犁体静摩擦因数均为0.6、土壤-土壤和土壤-犁体滚动摩擦因数分别为0.4、0.05。由于粘质土壤间存在一定粘结力，EDEM软件的Hertz-Mindlin with Bonding接触模型可较好模拟具有粘结力的土壤颗粒，因此本文选择该模型作为仿真接触模型。对试验用开畦沟前犁、船式开沟犁采用SolidWorks软件按1∶1建立三维模型导入EDEM软件中，位于长×宽×高为1 000 mm×500 mm×350 mm的虚拟土槽一侧，如图4所示。

图4 开畦沟装置EDEM仿真模型Fig.4 EDEM simulation model of ditching system

3.1.2土壤接触参数标定

选用Hertz-Mindlin with Bonding接触模型微观参数为：粘结法向刚度Sn、粘结切向刚度Sτ、粘结法向临界应力σmax、粘结切向临界应力τmax及颗粒粘结半径Rb。其中，粘结半径Rb反映湿颗粒含水率。前4个参数反映颗粒粘性，由于该模型的粘性刚度对颗粒行为不敏感，可取Sn=Sτ=5×107N/m3[15-16]。临界粘结应力不便于通过试验测得，本文采用虚拟标定试验与田间试验相结合方法进行标定。为减少标定参数个数，可取σmax=τmax[17]。

田间试验于华中农业大学现代农业科技试验基地展开，试验选取常年稻油轮作、平坦的地表，土壤含水率为25.47%、坚实度为823.9 MPa。试验机具及设备如图5所示，测试方法与文献[26]相同，调节限深轮高度控制开沟深度为300 mm，机组前进速度为1.2 m/s，通过BK-5型拉压力传感器测得组合式船型开畦沟装置平均牵引阻力为1 076.46 N。通过田间取样土壤测试其单轴压缩法向应力，试验结果表明法向应力为105Pa数量级。因此，虚拟标定试验时，设置犁体开沟深度为300 mm，前进速度为1.2 m/s。根据田间土壤含水率按文献[27]中计算方法确定粘结半径Rb为9.5 mm。在EDEM软件中设定如表3所示一系列梯度的临界应力，分别仿真开畦沟装置的平均牵引阻力，并与田间试验牵引阻力进行比较。由表3测试结果可知，设置σmax=τmax=3.5×105Pa时，误差最小，能较真实反映试验土壤与机具互作的力学特性。

图5 开畦沟装置田间测试装置Fig.5 Field testing device for ditching system1.机架 2.限深轮 3.开畦沟前犁 4.船式开沟犁 5.BK-5型下拉杆传感器 6.BK-5型上拉杆传感器

3.2 阻力特性仿真试验

3.2.1试验方法

分别选取结构参数相同，导曲线分别为直线型、抛物线型和指数曲线型的开畦沟前犁、船式开沟犁为仿真试验对象，探讨犁体曲面形状变化对牵引阻力的影响。3种导曲线类型的开畦沟前犁结构参数为：θmin=40°、Δθmax=5°、w=100 mm、h=350 mm、l=60 mm；船式开沟犁结构参数为：Φmin=67°、ΔΦmax=5°、Lz=300 mm、Hq=380 mm、wq=120 mm、lq=100 mm。上述3种导曲线类型犁体的曲面形状变化主要体现在曲面内蕴几何量E、L、M的变化趋势不同，将犁体结构参数代入表2中表达式计算可得E、L、M的变化规律。其中，由于常数变量τ的大小反映曲面纵向位置上的形状，对犁体曲面受力分析时常将所受合力作用点简化至中心处，故计算时取τ=0.5。设置EDEM中土壤模型为前文标定参数，犁体作业深度为300 mm，前进速度与驱动圆盘犁对置组合式耕整机的常规作业速度相同，为0.9～1.5 m/s[22]，仿真总时间为5 s，Rayleigh时间步长为20%，网格单元尺寸为最小颗粒半径的3倍。其中，0～2.5 s为颗粒生成及稳定阶段，2.5～5 s为犁体运动阶段。

表3 土壤颗粒临界应力校核Tab.3 Critical stress checking of soil particles

图6 牵引阻力及内蕴几何量E、L、M的变化曲线Fig.6 Variation trends of traction resistance and E, L and M

3.2.2试验结果分析

3种导曲线类型的开畦沟前犁、船式开沟犁牵引阻力随速度变化趋势及其内蕴几何量变化规律如图6所示。

由仿真试验结果可知，当犁体曲面结构参数一定时，在仿真速度范围内，开畦沟前犁、船式开沟犁牵引阻力的大小顺序均为：抛物线型、直线型、指数曲线型。抛物线型开畦沟前犁、船式开沟犁所受平均牵引阻力相比直线型分别低15.09%、16.92%，相比指数曲线型分别低32.59%、31.58%；在仿真速度由0.9 m/s增至1.5 m/s过程中，开畦沟前犁、船式开沟犁牵引阻力增长速率由大到小顺序均为：直线型、抛物线型、指数曲线型。直线型犁体近似匀速变化，抛物线型、指数曲线型变化速率越来越大；在整个仿真速度变化过程中，开畦沟前犁、船式开沟犁牵引阻力的波动程度(增长倍数)均为：直线型、抛物线型、指数曲线型，直线型开畦沟前犁、船式开沟犁牵引阻力分别增大了1.67、1.78倍，抛物线型犁体牵引分别增大了1.72、1.85倍，指数曲线型犁体牵引阻力分别增大了1.97、2.02倍，抛物线型与直线型犁体牵引阻力的波动程度相差不大。

由图6b、6f中内蕴几何量E的变化规律可知，直线型犁体的内蕴几何量E均为定值，抛物线型和指数曲线型犁体的E值变化速率越来越大，且指数曲线型犁体的E值变化速率更大，犁体内蕴几何量E的变化速率与其牵引阻力随速度的增长速率的变化规律一致；由图6c、6g中内蕴几何量L的变化规律可知，抛物线型犁体的L单调递减，直线型犁体L为定值，指数曲线型犁体L单调递增，当犁体的L为单调递减变化时，牵引阻力较小；由图6d、6h中内蕴几何量M的变化规律可知，M的波动程度大小(增量)均为：直线型、抛物线型、指数曲线型，与犁体牵引阻力的波动程度(增长倍数)变化规律一致。根据仿真试验及前文曲面微分几何性质分析，当导曲线类型一定时，曲面结构参数变化不会影响内蕴几何量的变化趋势，故内蕴几何量E、L、M可分别反映犁体阻力随速度的增长速率、犁体牵引阻力大小、犁体阻力随速度的波动程度。因此，在设计水平直元线形成的犁体曲面时，如果设计的犁体导曲线形状能使曲面内蕴几何量E的变化率较小、L为单调减函数、M的波动较小，可使犁体具有较好的减阻性能。根据上述分析，本文设计开畦沟前犁、船式开沟犁的导曲线为抛物线时，相比直线型、指数曲线型犁体，其主要触土曲面内蕴几何量E、L、M可处于更优变化范围内，犁体牵引阻力更小。

3.3 参数优化试验

通过阻力特性试验分析可知，在驱动圆盘犁对置组合式耕整机作业速度范围内，抛物线型犁体具有更好减阻特性。由前文主要触土曲面设计与分析可知，在部分结构参数一定时，除导曲线类型外，开畦沟前犁宽度w、船式开沟犁整形曲面最大元线角Φmax为影响开畦沟装置牵引阻力的主要因素。本文以抛物线型犁体为试验对象，选取上述二者为试验因素，开畦沟装置总牵引阻力Fd为评价指标，开展开畦沟装置主要触土曲面参数优化试验，仿真试验时固定犁体作业深度为300 mm、作业速度为1.2 m/s，试验因素编码如表4所示。

表4 试验因素编码Tab.4 Experimental factors and levels

3.3.1试验结果

试验结果与方差分析结果如表5、6所示。

表5 试验方案与结果Tab.5 Design and results of experiments

表6 方差分析结果Tab.6 Results of variance analysis

注：** 和*分别表示方差分析在0.01和0.05水平上显著。

应用Design-Expert软件对试验数据进行分析处理，由方差分析结果知，模型显著性试验F值为72.81，P值小于0.000 1，决定系数R2为0.973 3，表明回归模型显著、拟合程度较好。前犁犁体宽度w、整形曲面最大元线角Φmax均对牵引阻力有显著影响，通过二次多元回归拟合的回归模型为

Fd=83 971.890 6+33.905 88w-2 548.498 67Φmax-

(11)

3.3.2结果优化

以开畦沟装置牵引阻力最小为目标，前犁犁体宽度w、整形曲面最大元线角Φmax为变量，建立参数优化数学模型。目标函数和约束条件为

(12)

利用Design-Expert软件进行求解，得出前犁犁体宽度w为92 mm、整形曲面最大元线角Φmax为66°时，开畦沟装置最小牵引阻力为1 042.52 N。

4 田间试验

为验证仿真试验结果及考察曲面参数优化的组合式船型开畦沟装置作业效果，在华中农业大学现代农业科技试验基地开展田间试验。试验机具为驱动圆盘犁对置组合式耕整机，试验动力为东方红LX954型拖拉机，试验田块常年稻油轮作，平均土壤坚实度为848.4 kPa，平均土壤干基含水率为24.7%。试验仍用前文使用的BK-5型拉压力传感器(图7a)测试开畦沟装置牵引阻力。试验时，通过调节限深轮控制犁体开沟深度为300 mm，调节拖拉机挡位和手油门测试开畦沟装置在机组前进速度为0.9、1.2、1.5 m/s时的牵引阻力，测试方法参照文献[23,26]。

图7 田间试验Fig.7 Field experiments1.动态数据采集器 2.BK-5型上拉杆传感器 3.BK-5型下拉杆传感器

田间试验效果与牵引阻力测试结果如图7和表7所示。试验结果表明，组合式船型开畦沟装置在3种作业速度下测试的平均牵引阻力分别为956.77、1 101.33、1 564.85 N，与仿真试验误差均在7%以内。开畦沟装置均能开出平均沟深为294.8 mm、平均沟宽为384.6 mm的梯形畦沟，并能有效将驱动圆盘犁形成的内侧犁沟填埋，作业效果满足油菜播种开畦沟农艺要求。

表7 田间试验结果与分析Tab.7 Analysis and results of field experiments

5 结论

(1)开展了驱动圆盘犁对置组合式耕整地开畦沟装置主要触土曲面的牵引阻力分析和曲面参数分析，确定了主要触土曲面(前犁犁体曲面、整形曲面)的主要结构参数范围。基于微分几何理论，建立了能量化描述不同导曲线类型(直线、抛物线、指数曲线)犁体曲面形状变化差异的微分几何内蕴量E、L、M表达式。

(2)阻力特性仿真试验表明：犁体曲面内蕴几何量E、L、M可分别反映犁体阻力随速度的增长速率、犁体牵引阻力、犁体阻力随速度的波动程度。当设计犁体的导曲线形状能使曲面内蕴几何量E的变化率较小、L为单调减函数、M的波动较小时，犁体具有较好的减阻性能。在犁体曲面结构参数一定，作业速度v为0.9～1.5 m/s时，导曲线为抛物线型的开畦沟前犁、船式开沟犁具有较好的减阻特性。

(3)参数优化仿真试验表明：在作业速度为1.2 m/s、抛物线型开畦沟前犁宽度为92 mm、船式开沟犁整形曲面最大元线角为66°时，开畦沟装置牵引阻力最小，为1 042.52 N。

(4)田间试验表明，经参数优化的组合式船型开畦沟装置在作业速度为0.9、1.2、1.5 m/s时测试的平均牵引阻力分别为956.77、1 101.33、1 564.85 N，与仿真试验结果误差在7%以内，作业效果满足油菜播种开畦沟的农艺要求。