大角速度条件下星像运动轨迹建模及误差评估

何贻洋，王宏力，冯磊，*，由四海，陈志侃

（1.火箭军工程大学 导弹工程学院，西安710025； 2.中国人民解放军66133部队，北京100144）

星敏感器作为一种姿态测量设备，具有精度高、自主性好以及无误差漂移等优点，因而在航空航天领域具有重要的应用价值［1-2］。星敏感器通常捷联安装于弹道导弹、卫星等载体上，若存在大姿态角机动或者受到外界环境影响时，由于目前星敏感器的动态性能仍然较差，星敏感器拍摄的星图会模糊，这可能严重影响星点提取成功率和精度，进而降低星图识别成功率，甚至可能导致星敏感器无法正常定姿［3-5］。

经典的模糊图像复原方法主要分为以下两大类：盲复原方法和非盲复原方法。由于星图的先验信息可以基于惯导信息等获取，因而在模糊星图复原的研究中，非盲复原方法应用更为广泛［6-10］。模糊核函数是非盲复原方法的基础，而分析星图模糊的机理是获得模糊核函数的第一步。文献［11-13］将星图模糊机理近似为成像平面的匀速直线运动，利用Radon变换、倒频谱分析等方法得到星图模糊的尺度和方向，从而估计模糊星图的点扩散函数。文献［14-15］研究了转动条件下成像平面上的星像运动轨迹，给出星像运动轨迹近似为一段直线的结论，但对于星像运动轨迹形式分析并不全面。李楠和路小波［16］研究了散焦和运动模糊的复合模型，提出了一种基于自相关的参数估计方法，在一定程度上减轻了混叠现象带来的干扰。文献［17］中采用功率谱密度函数的方法分析了载体振动对星敏感器成像的影响，可以较好地模拟星图的振动模糊效果，这也为星图模糊的研究提供了新思路。文献［18］提出了一种基于线段扩散函数的星像能量分布模型，为星图模糊机理的研究开辟了新思路，但仍是基于星像运动轨迹为直线这一前提的。可见不少文献中都将星像运动轨迹当做匀速直线运动来处理，但实际上星像运动轨迹随着载体运动形式的不同而各异。故而吴小娟和王新龙［3］对于绕光轴和非光轴转动时成像平面上的星像运动轨迹进行了建模分析（光轴指星敏感器测量坐标系Osxsyszs的Oszs轴，非光轴指垂直光轴方向的Osxs轴和Osys轴），但对于绕任意方向转动时的星像运动轨迹形式未做进一步分析。目前对星图模糊的研究主要聚焦于模糊核函数估计和模糊复原算法，而星像运动对星点提取精度影响是怎样的？将产生多大影响？这些问题鲜有提及，但实际上这是研究星图模糊对星敏感器性能影响时应该首先回答的问题。

本文针对大角速度条件下星敏感器星像拖尾的问题，对星像运动轨迹的数学模型进行了研究，并定量评估了星像运动对星点提取精度影响的大小，为提高星敏感器在复杂工作环境下的动态性能提供参考。

1 星像运动轨迹建模

根据文献［3］的研究结果，在曝光时间内，当绕非光轴转动时，星像运动轨迹近似为匀速直线运动的一段；当绕光轴转动时，星像运动轨迹为一段圆弧，而实际中星敏感器转动可绕任意方向。故本文对绕星敏感器测量坐标系内任意方向转动时的星像运动轨迹进行分析建模。

绕星敏感器测量坐标系Osxsyszs内任意方向转动时，可将角速度分解到Osxsyszs3个坐标轴上，结合文献［3］的相关成果，可知在曝光时间内，星像在成像平面上的运动为匀速直线运动和定轴匀角速度运动的叠加。为了方便描述星像运动轨迹，将星像在成像平面上匀速直线运动速度分量 记 为v0x＞0，v0y＞0，v0x≈fωy／dCCD［3］，v0y≈fωx／dCCD。f为星敏感器焦距；ωx、ωy和ωz分别为绕Osxs、Osys和Oszs转动角速度；dCCD为星敏感器成像平面像元物理尺寸。不妨设星像在成像平面上的定轴匀角速度运动沿顺时针方向，角速度记为ωz，星像初始位置位于成像平面的Oy轴上，星像运动示意图如图1所示。

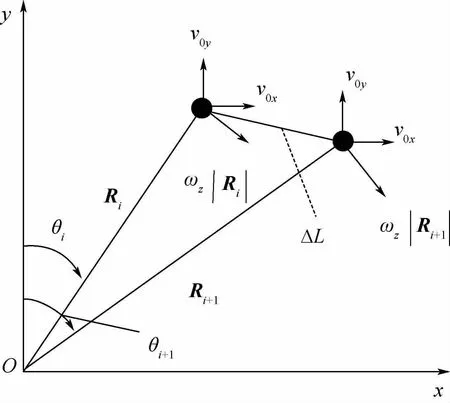
图1 绕任意轴方向转动时的星像运动示意图Fig.1 Schematic diagram of star spotmotion when rotating around any axis

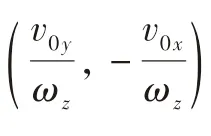
首先给出圆的微分方程，不妨设圆心为（a，b）、半径为R的圆方程为

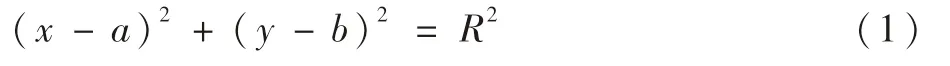
对x求导，整理可得圆的微分方程为

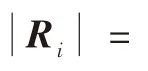
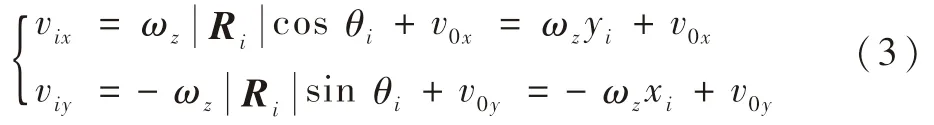
由于Δt非常小，则可近似认为在Δt时间内，星点在成像平面上的运动速度不变，则从第i→i＋1时刻，星点的位移量为

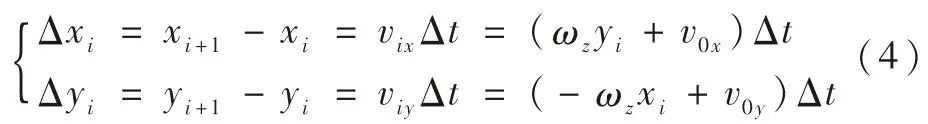
由式（4）可得

式（5）实质上为导数的定义，因此有

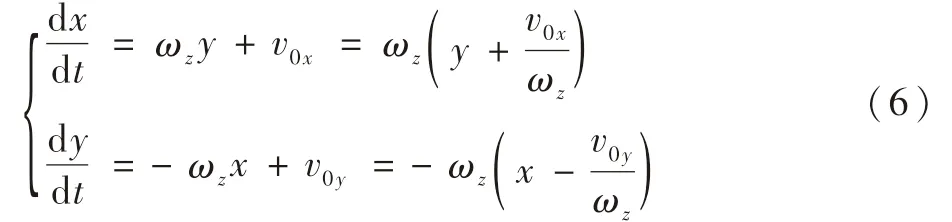
将式（6）中参数t消去，得到运动轨迹的微分方程为

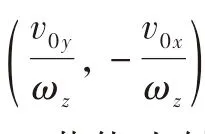
若绕光轴的角速度接近于零，根据式（7），可知星像运动轨迹的圆心位置位于无穷远处，那么此时形成的圆弧即为一段直线，这与文献［3］中绕非光轴转动时的星像运动轨迹为一段直线的结论相一致。所以，无论转动轴指向如何，星像在成像平面上的运动轨迹都可认为是一段圆弧。

2 星像运动对星点提取精度影响评估

2.1 星像运动时的能量分布建模

对于静态条件下的星图，星像在像平面上的能量分布符合二维高斯分布，数学表示为

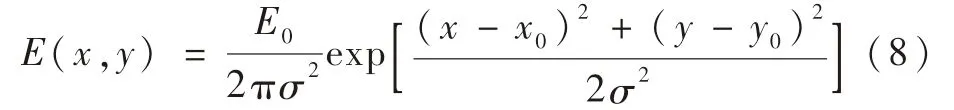
式中：E0为曝光时间内星点的总能量；（x0，y0）为星点位置；（x，y）为星图上的某个像素点；σ为高斯弥散斑半径，代表了能量弥散程度，σ越大，星像能量越分散，根据二维高斯分布的特点以及3σ准则，星像99%以上的能量集中于距离星点的3σ范围以内。

当星敏感器处于动态环境下，星像在像平面上会产生拖尾现象，星像的能量不再符合二维高斯分布。值得注意的是，在星敏感器镜头参数确定的情况下，在一次曝光时间内星像的总能量可认为不变，但在星像运动轨迹上能量将按照某种规律进行分布。下面对星敏感器处于动态情况下，星像的能量分布进行建模分析。

将星敏感器曝光时间Te等分为N个区间［ti，ti＋1］，i＝0，1，…，N－1，Δt＝ti＋1－ti＝Te／N，t0＝0，tN＝Te，Te内星像的总能量为E0，由于每个时间区间［ti，ti＋1］非常小，因而可以认为在［ti，ti＋1］内星像的能量仍服从二维高斯分布，不妨设在［t0，t1］的星像质心坐标为（x0，y0），那么在［ti，ti＋1］内的星像质心点坐标为（xi，yi），i＝0，1，…，N－1。在［ti，ti＋1］时间内，星像能量分布为

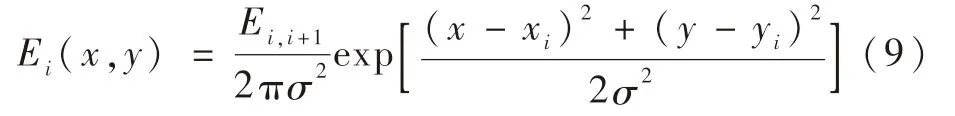
式中：Ei，i＋1＝E0／N。

假设上述高斯分布的弥散斑半径相等，将各个微小曝光时间内的星像能量分布函数进行叠加，得到星像总的能量分布函数为

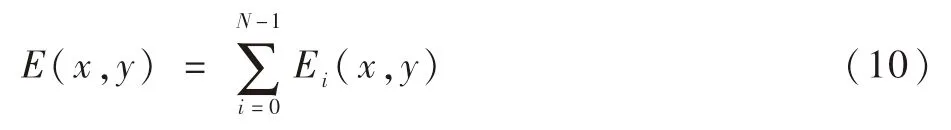
为了更直观展示星图模糊情况下星像的能量分布情况，在绕星敏感器测量坐标系Osxsyszs的坐标轴转动的条件下，假设E0＝1，σ＝0.5，得到绕Osxs、Osys和Oszs轴转动时，模糊星图上星像能量分布的仿真示意图如图2所示。由图2可知，在（a）、（b）条件下，星像运动轨迹为一段直线；在（c）、（d）条件下，星像运动轨迹为一段圆弧。模糊星像不再是符合二维高斯分布的高斯弥散斑，而是呈带状分布。

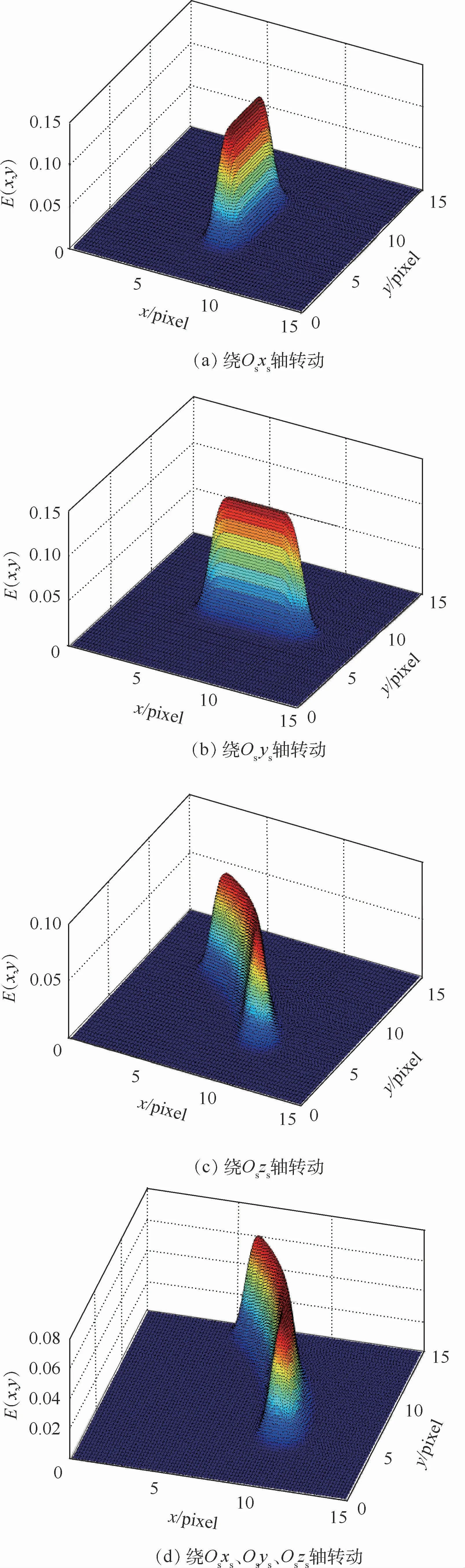
图2 模糊星图上星像能量分布仿真示意图Fig.2 Schematic diagram of star spot energy distribution simulation on blurred star image

2.2 星像运动对星点提取精度影响的评估分析

基于灰度的算法将星点等同于星像灰度分布区域的灰度极值点，利用灰度分布信息求取其质心的精确坐标，是目前常用的星点提取算法，如质心法、高斯曲面拟合法等［5］。

质心法将星像区域内像元的灰度值作为其坐标的权重，然后计算星像区域的一阶矩，得到星点坐标。高斯曲面拟合法要求星像灰度分布区域近似服从二维高斯分布，才能获得较高星点提取精度，高斯曲面拟合方法显然不再适用于星像模糊严重的情形。因此，本文着重研究由转动引起的星图运动模糊现象对质心法提取精度的影响。

质心法的计算窗口取为一矩形区域，这一区域的左上角像元坐标设为（1，1），右下角的像元坐标为（m，n）。不妨设G（x，y）为像元（x，y）处的灰度，与该像元的能量成正比，有G0～E0，Gi～Ei，i＋1；根据2.1节可知，每个微小曝光时间区间对应的星像灰度近似服从二维高斯分布，且星像光斑绝大部分能量集中于距离星点坐标3σ范围以内。那么质心法的计算窗口应能够包含所有的（xi－3σ，xi＋3σ）＆（yi－3σ，yi＋3σ）区域。

结合式（9）、式（10）则有式（11）～式（14）成立：

（xi，yi）为［ti，ti＋1］内的星像质心坐标，利用质心法可以得到（xi，yi）的计算公式如下：

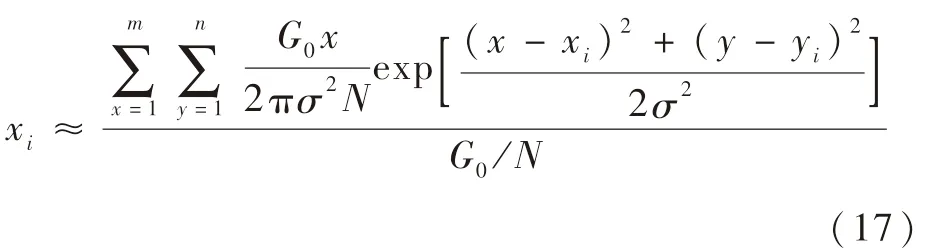
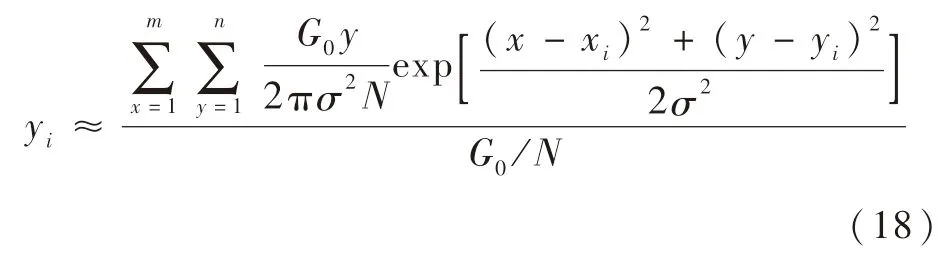
将式（17）、式（18）分别代入式（15）、式（16），则有

下面 分 析（x′0，y′0）与 静 态 条 件 下 星 点 坐 标（x0，y0）之间的误差与星像运动轨迹长度之间的关系。

星点坐标误差的模定义如下：

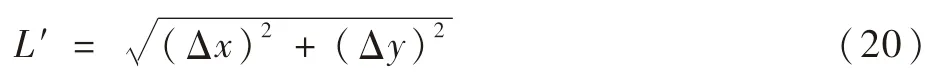
式（20）表示实际提取的星点与理想的星点之间的距离。

下面对绕非光轴和光轴转动的情况下星图模糊引起的星点坐标误差进行评估分析。

1）绕非光轴转动时星图模糊引起的星点坐标误差评估

绕非光轴转动时，星像在成像平面上的运动近似为匀速直线运动，假设星像在成像平面的Ox及Oy轴上的运动速度分别为vx、vy，则在曝光时间 Te内，星 像 模 糊 的 长 度 为 L1＝

式中：i＝0，1，…，N－1；Δt＝ti＋1－ti。

可得

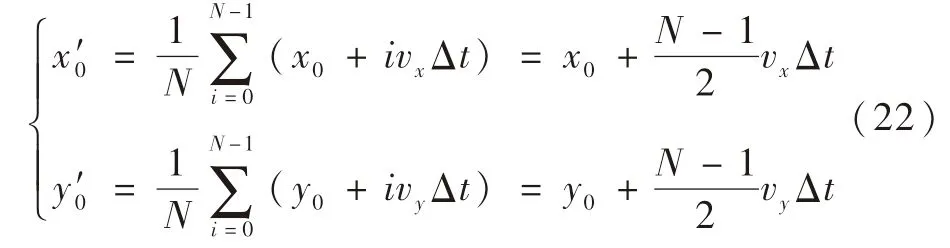
得到星像运动引起的星点坐标误差为

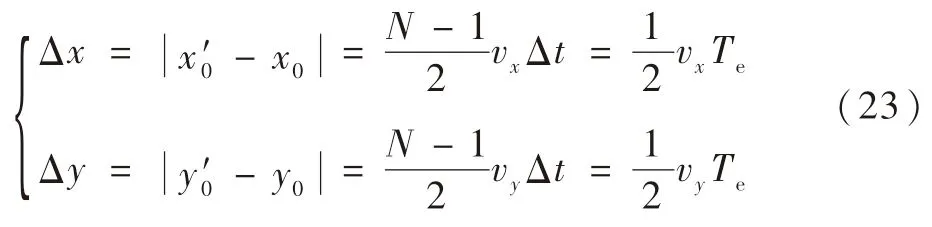
2）绕光轴转动时星图模糊引起的星点坐标误差评估

绕光轴转动时，星像在成像平面上作圆周运动，设绕光轴运动的角速度为ωz；星像逆时针做圆周运动，星像圆周运动半径记为r，曝光时间Te分割为N个等距的微小时间区间Δt；在Δt内，星像模糊的长度l＝rωzΔt，那么Te内星像运动轨迹长度L2＝（N－1）l（也可根据式（4）迭代计算L2），不妨设初始质心（x0，y0）与像平面Ox轴的夹角为β0，对于第i个Δt对应的质心坐标（xi，yi），i＝0，1，…，N－1可表示为

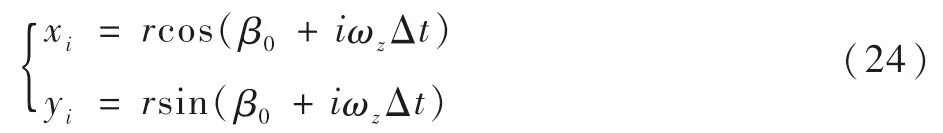
由于星像在Te内所转动的角度ωzTe为小量，可做如下近似：cos（iωzΔt）≈1，sin（iωzΔt）≈iωzΔt，将式（24）三角函数展开后简化为

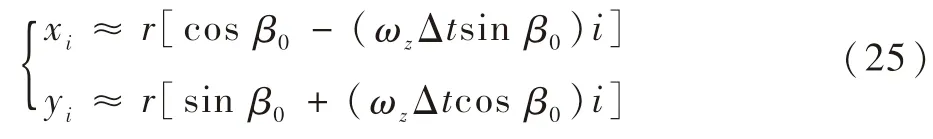
将式（25）代入式（19）中，则有

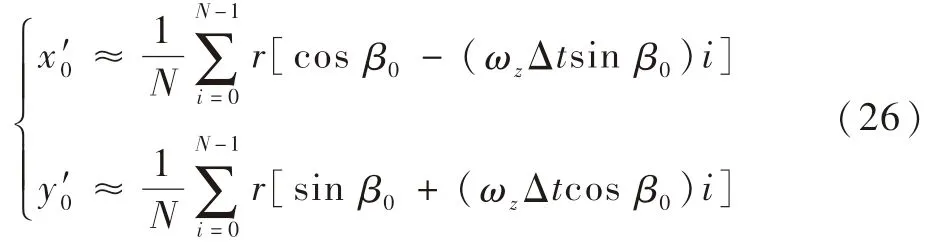
得到星图运动模糊引起的星点坐标误差为

根据式（27）、式（28）可知，当绕光轴转动时，利用质心法获得的星点坐标（x′0，y′0）与（x0，y0）之间的误差（Δx，Δy）与β0有关，星点坐标误差的模L′2近似为星像运动轨迹长度L2的一半，不随β0而改变，但与（x0，y0）与主点之间的距离有关，距离主 点 越 远，L2越 大，星 点 误 差 的 模也 就越大。

当绕任意方向转动时，星像在成像平面上的轨迹仍然为一段圆弧，根据上述分析推导可知，星点坐标误差的模仍可用星像运动轨迹长度L3的二分之一来衡量。在此不再赘述。

在实际应用中，将星敏感器相关参数代入式（4）计算星像运动轨迹长度，根据本文结论，可迅速估计出由于星图模糊引起的星点坐标误差，若星图模糊引起的星点坐标误差较小，不影响后续的星图识别和定姿，则不需进行模糊星图复原，否则需对模糊星图进行复原，以保证星敏感器正常工作。所以本文为评估星敏感器是否需要启用模糊星图复原算法提供了参考。

3 仿真实验验证

3.1 基本条件设置

星敏感器视场大小设置为9°×9°，焦距为65.76 mm，像元大小为20μm，面阵大小为512 pixel×512 pixel，曝光时间为100ms，星敏感器镜头孔径为0.04m；从SKY2000主星表筛选出星等小于6的导航星，并剔除其中的双星与变星，剩余4 908 颗导航星组成本文的星表。利用Monte Carlo方法随机产生星敏感器的一个光轴指向，其在天球坐标系下的赤经、赤纬为（36°，50°）；星图模拟仿真实验中加入的高斯白噪声均值为0，均方差为6（灰度范围为0～255）。

3.2 实验分析

在3.1节的仿真条件下，静态、无噪声情况下获得一幅理想的星图如图3所示；静态、有噪声情况下获得一幅星图如图4所示。选取星图中3个具有代表性的星像进行比较，记为star1、star2和star3。star1位于中心区域，靠近主点；star2位于边缘区域；star3介于star1和star2之间的区域，这3个星像可反映成像平面上的不同区域受星图模糊影响的情况。

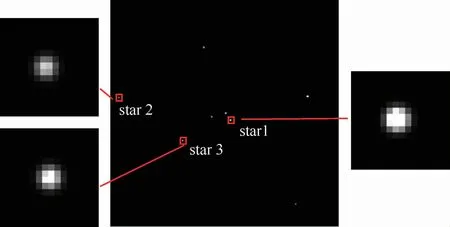
图3 静态无噪声条件的理想星图Fig.3 Ideal star image under static noise-free conditions

图4 静态有噪声条件的星图Fig.4 Star image under static and noisy conditions

设置以下4组角速度大小和方向，每组条件下仿真5次：①绕星敏感器测量坐标系的Osxs轴转动，角速度为1，2，3，4，5（°）／s；②绕星敏感器测量坐标系的Osys轴转动，角速度为－1，－2，－3，－4，－5（°）／s；③绕星敏感器测量坐标系的Oszs轴 转 动，角 速 度 为8，10，12，14，16（°）／s；④绕星敏感器测量坐标系的三轴转动，绕Osxs轴转动角速度为1，2，3，4，5（°）／s，绕Osys轴转动角速度为－1，－2，－3，－4，－5（°）／s，绕Oszs轴转动角速度为8，10，12，14，16（°）／s。其余仿真条件不变，得到star1、star2和star3的运动模糊情况，分别如图5～图8所示。

图5 绕O s x s轴转动时star1、star2和star3的运动轨迹Fig.5 Motion trajectory of star1，star2 and star3 when rotating around O s x s axis

图6 绕O s y s轴转动时star1、star2和star3的运动轨迹Fig.6 Motion trajectory of star1，star2 and star3 when rotating around O s y s axis

图7 绕O s z s轴转动时star1、star2和star3的运动轨迹Fig.7 Motion trajectory of star1，star2 and star3 when rotating around O s z s axis

图8 绕O s x s、O s y s和O s z s轴转动时star1、star2和star3的运动轨迹Fig.8 Motion trajectory of star1，star2 and star3 when rotating around O s x s，O s y s and O s z s axis

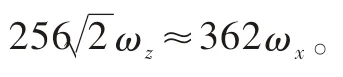
为了验证本文关于星像运动对星点提取影响评估研究所得结论的正确性，进行了仿真实验验证。设置了以下3种转动的仿真条件：

1）绕Osxs轴角速度ωx＝5sin（πt／2）；

2）绕Oszs轴角速度ωz＝16sin（πt）；

3）绕Osxs轴角速度ωx＝5sin（πt／2），绕Osys轴角速度ωy＝－6sin（πt／3），绕Oszs轴转动角速度ωz＝16sin（πt）。

3种仿真条件中的角速度变化如图9所示。

以曝光时间0.1 s作为采样周期，仿真时间为6 s，得到如下仿真结果。

1）第1组：仿真条件1）下star1、star2和star3的星点坐标误差结果和星点坐标误差的模与星像运动轨迹长度二分之一的对比，如图10、图11所示。

2）第2组：仿真条件2）下star1、star2和star3的星点坐标误差结果和星点坐标误差的模与星像运动轨迹长度二分之一的对比，如图12、图13所示。

3）第3组：仿真条件3）下star1、star2和star3的星点坐标误差结果和星点坐标误差的模与星像运动轨迹长度二分之一的对比，如图14、图15所示。

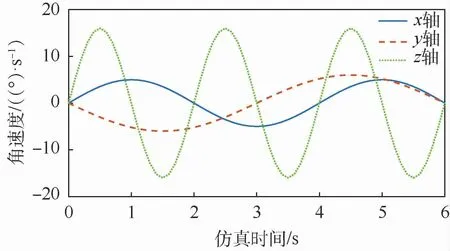
图9 仿真条件下的角速度变化曲线Fig.9 Angular velocity curves under simulation conditions

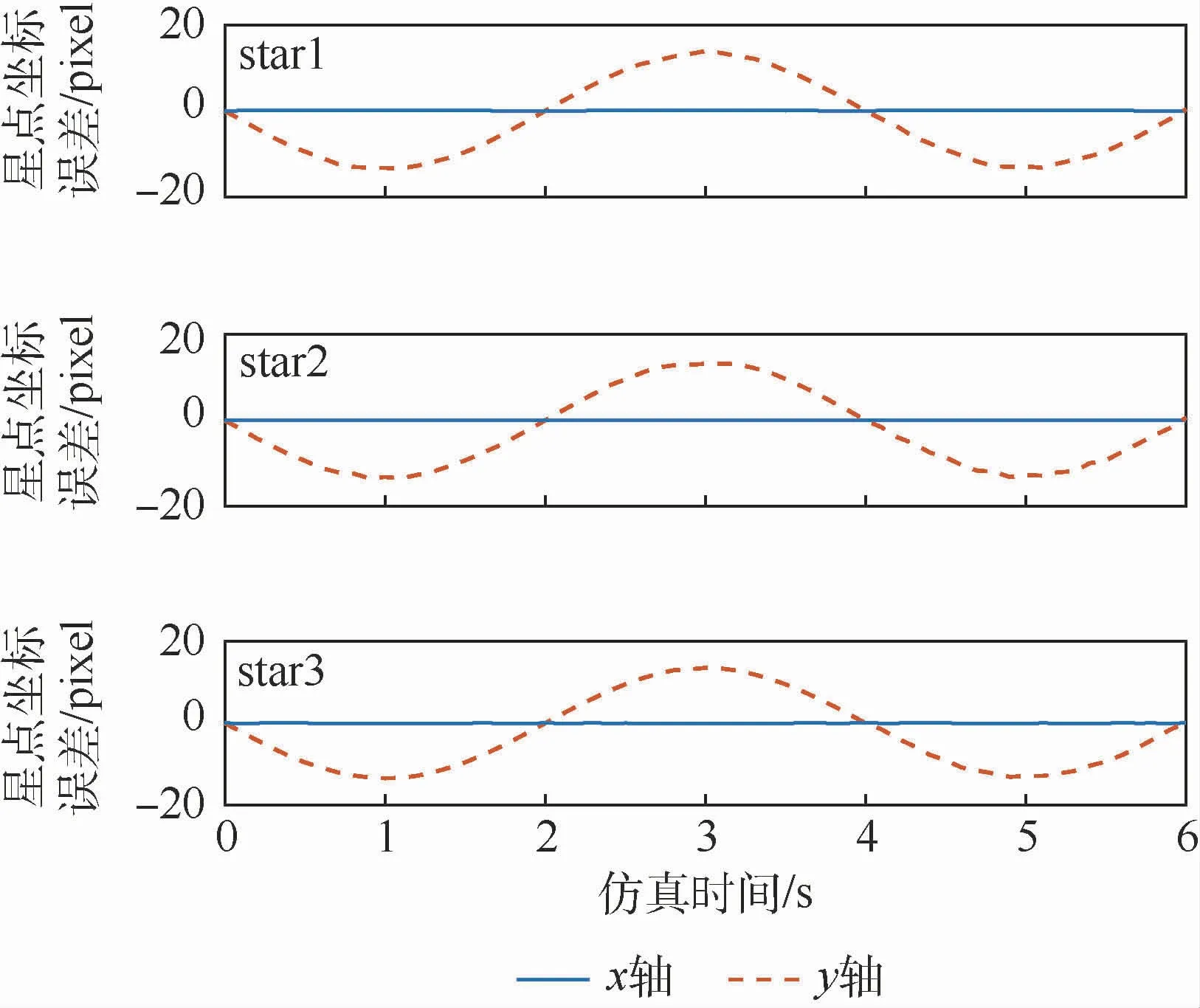
图10 仿真条件1）的星点坐标误差Fig.10 Star spot coordinate error under simulation condition 1）

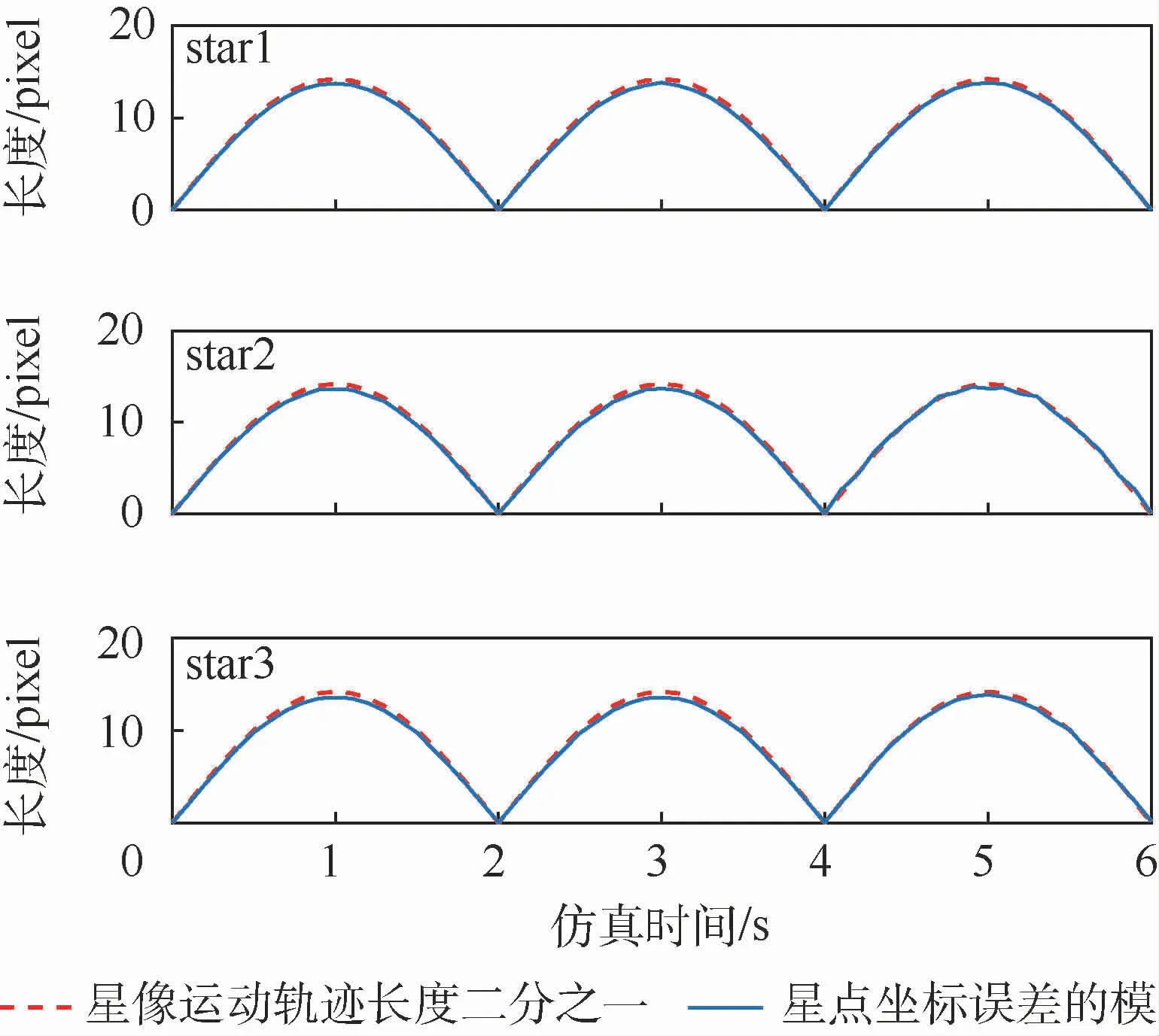
图11 仿真条件1）的星点坐标误差的模与星像运动轨迹长度二分之一的对比Fig.11 Comparison ofmodulus of star spot coordinate error and one half of star spotmotion trajectory length under simulation condition 1）

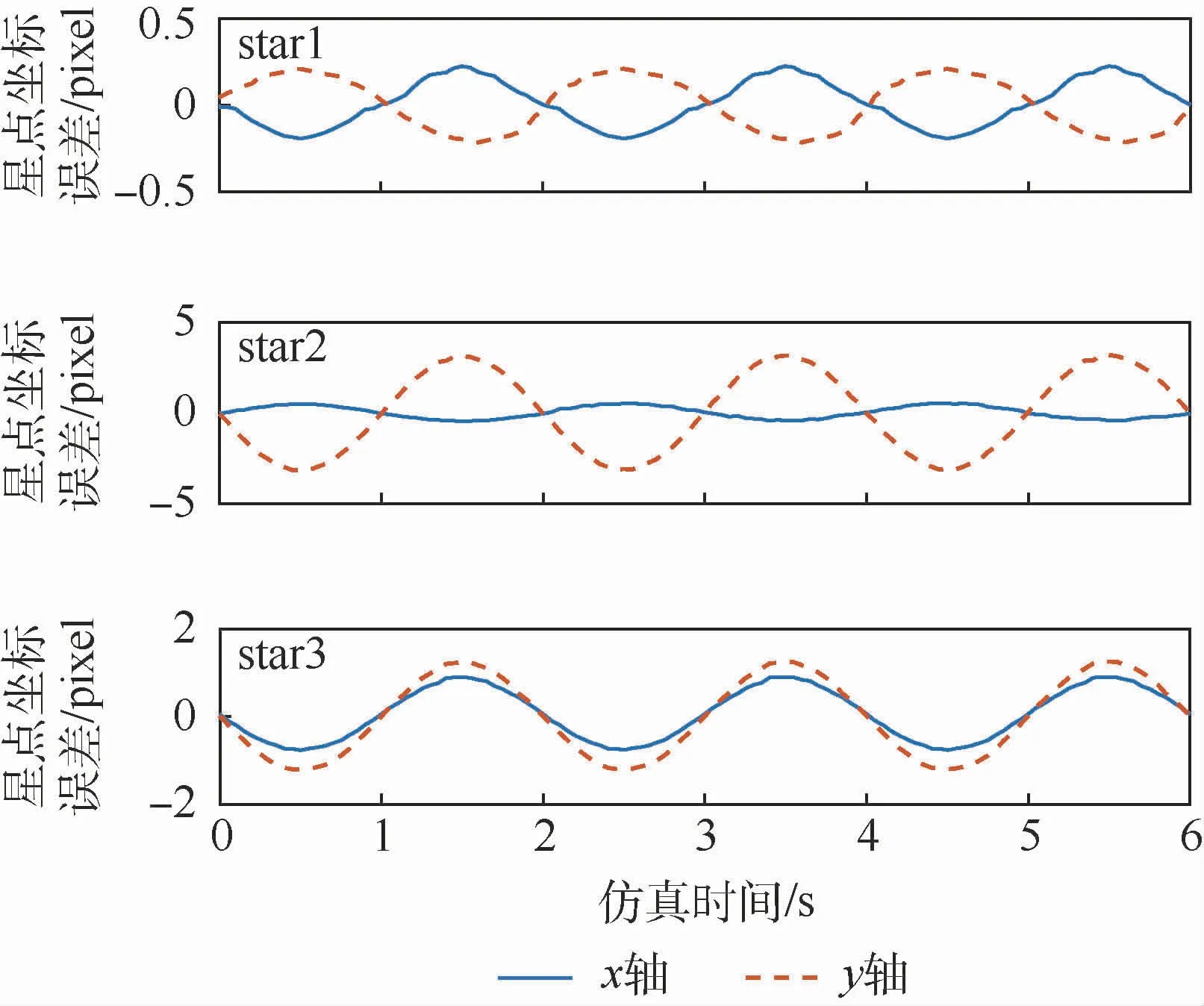
图12 仿真条件2）的星点坐标误差Fig.12 Star spot coordinate error under simulation condition 2）

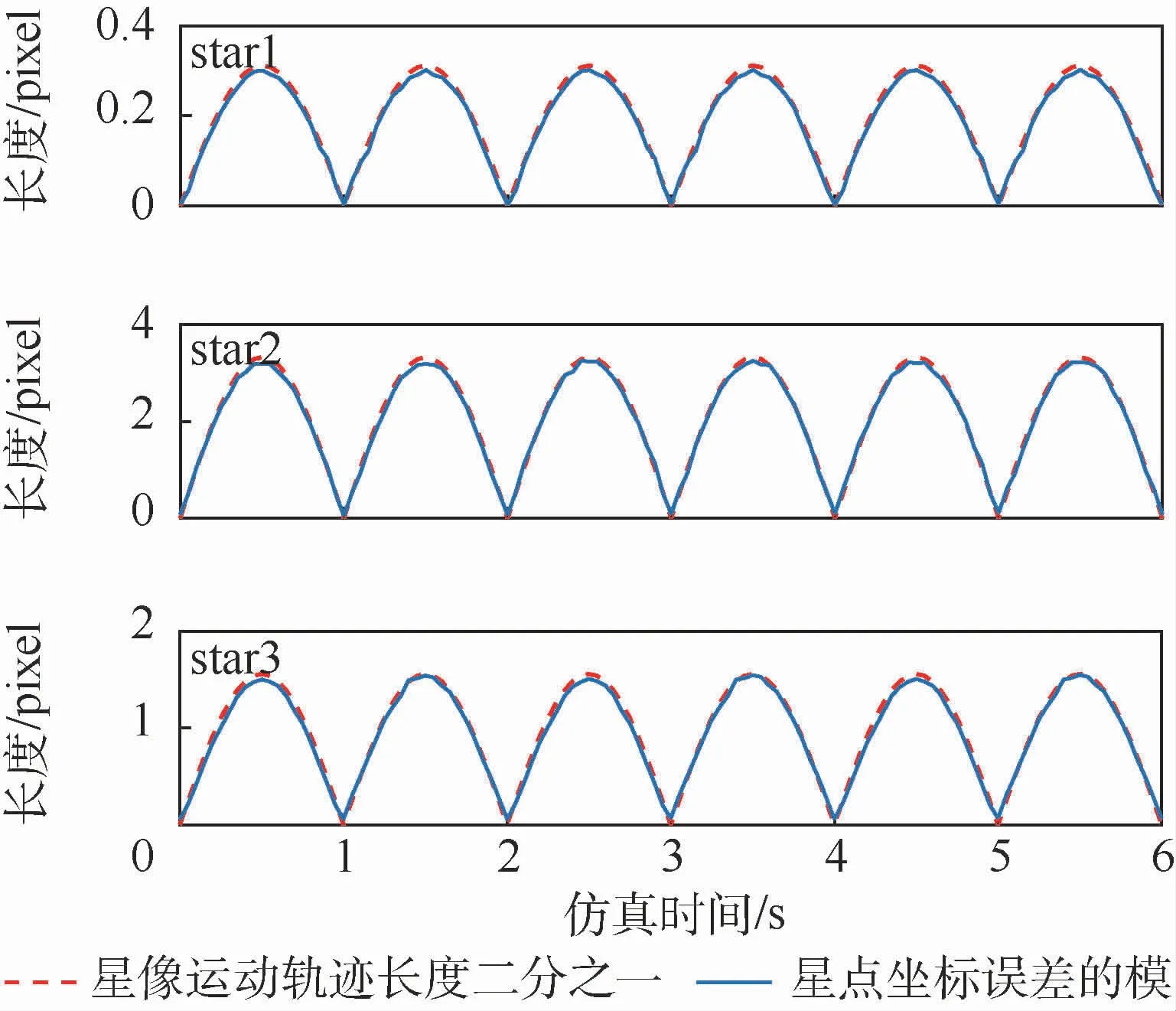
图13 仿真条件2）的星点坐标误差的模与星像运动轨迹长度二分之一的对比Fig.13 Comparison ofmodulus of star spot coordinate error and one half of star spotmotion trajectory length under simulation condition 2）

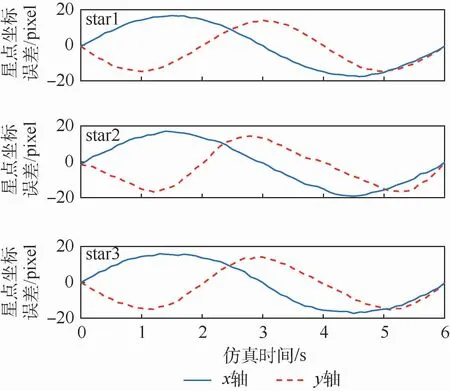
图14 仿真条件3）的星点坐标误差Fig.14 Star spot coordinate error under simulation condition 3）

图15 仿真条件3）的星点坐标误差的模与星像运动轨迹长度二分之一的对比Fig.15 Comparison ofmodulus of star spot coordinate error and one half of star spotmotion trajectory length under simulation condition 3）

绕星敏感器测量坐标系Osxs轴转动时的星点坐标误差结果如图10所示，此时star1、star2和star3的x轴坐标误差几乎都为零，3个星像的y轴坐标误差曲线的变化规律一致，可见绕非光轴转动对星图不同区域星像的影响大小是一样的，与星像在星图上的位置无关；绕星敏感器测量坐标系Oszs轴转动时的星点提取误差结果如图12所示，star1、star2和star3坐标误差曲线的幅值和相位各不相同，这取决于星点与主点的相对位置，star1距离主点最近，其坐标误差曲线的幅值最小，而star2距离主点最远，其坐标误差曲线的幅值最大；绕星敏感器测量坐标系三轴转动时的星点提取误差结果如图14所示，3个星点的x轴坐标误差变化周期与绕Osys轴角速度ωy的变化周期接近，3个星点的y轴坐标误差变化周期与绕Osxs轴角速度ωx的变化周期接近，可见在本文仿真条件下绕Oszs轴角速度ωz带来的影响远远小于绕Osxs、Osys轴角速度的影响。图11、图13和图15是3种仿真条件下，star1、star2和star3坐标误差的模与其运动轨迹长度二分之一的对比，可见无论角速度大小和方向如何，星像运动对星点提取精度的影响都可近似用星点运动轨迹长度二分之一来衡量评估。这也验证了本文结论的正确性和有效性。

4 结 论

本文建立了星敏感器绕任意方向转动时在成像平面上星像运动轨迹的数学模型，得到了此时的星像运动轨迹仍是一段圆弧的结论；在此基础上，基于微元思想建立了星像运动时的能量分布模型，推导出质心法的星点提取误差的模近似为星点运动轨迹长度二分之一，这可为定量评估星像运动对星点提取影响的大小提供重要的理论参考。本文结论也说明了星图模糊确实会影响星敏感器的工作性能，开展模糊星图复原的研究是十分必要的。