基于快速模拟退火的组合聚类算法
2019-09-10李红张志宾
李红,张志宾
(北京航空航天大学 经济管理学院,北京100083)
组合聚类旨在融合多个聚类结果以获得比传统聚类方法更好的样本划分。一方面,组合聚类相当于基础聚类结果的加权平均,对噪声、孤立点和抽样变化不敏感,且聚类不稳定性能从组合分布中得到弥补,从而使组合聚类结果具有更好的鲁棒性[1];另一方面,组合聚类在搜索最优解的过程中,有可能找到比所有基础聚类都好的划分结果,使组合聚类结果具有一定的新颖性。
近年来,国内外学者提出了多种组合聚类实现模型,一般可分为如下几类:图/超图划分方法、协联矩阵法、投票法、组合优化法及启发式求解等。
超图划分方法始于Strehl和Ghosh[2]的开创性工作,该研究设计并同时使用3种方法:CSPA(Cluster-based Sim ilarity Partitioning A lgorithm)、HGPA(Hyper Graph Partitioning Algorithm)和MCLA(Meta-Clustering A lgorithm),以返回最优的组合聚类结果。随后,若干学者对上述模型做了多方向扩展,如Ayad[3]、Yang和Kamel[4]分别使用近邻法和蚁群算法扩展了CSPA模型。除超图外,二分图划分、近邻传播等方法也被用于组合聚类研究[5-6]。
协联矩阵法根据基础聚类计算样本之间的相似度或距离,生成协联矩阵并在其上完成组合聚类。该方法最早由Fred和Jain[7]提出,其协联矩阵由投票机制产生;Wang等[8]在生成协联矩阵时进一步考虑了簇的大小因素;Hu等[9]引入序贯三支决策方法来构建协联矩阵;Liu等[10]提出了基于协联矩阵的谱聚类方法;Huang等[11]提出了局部加权的组合聚类策略。
投票法通过投票和重标记策略获取组合聚类结果。例如,Zhou和Tang[12]基于多种投票策略对基础聚类进行组合;Fu等[13]建立了模糊投票矩阵和多数仲裁者度量,并利用其获取组合聚类结果;陈晓云和陈刚[14]提出了加权投票的聚类集成方法。
组合优化法建立组合聚类目标函数,通过优化问题求解,最大化组合聚类与基础聚类集的相似性。由于全局最优解搜索是一个NP-hard问题,模拟退火[15]、因子图[16]、最大期望(Expectation Maximization,EM)算法[17]等方法被用于求解近似最优解。模拟退火是近似求解组合优化问题的经典方法,被广泛用于分类和聚类问题[18-19]。Lu等[15]对模拟退火在组合聚类中的应用进行了探索,提出了标签变更时目标函数的增量计算方法,但其标签变更采用了随机选择策略,算法收敛较慢。
无论何种方法,各基础聚类获得的样本划分结果都是组合聚类的重要先验信息。本文利用基础聚类对样本划分的完全或部分一致性,构建了基于投票的快速模拟退火(Rapid Simulated Annealing Based on Voting,BV-RSA)模型,该模型引入超点运动和投票箱机制来约束退火过程中的节点运动模式,实现组合聚类近似最优解的快速搜索。
1 BV-RSA模型框架
给定数据样本集X={x1,x2,…,xn},一组基础聚类集Π ={π1,π2,…,πr},基础聚类矩阵为Zn×r,矩阵元素zij为数据样本xi在基础聚类πj中的簇标签,组合聚类通常被形式化为如下的组合优化问题:
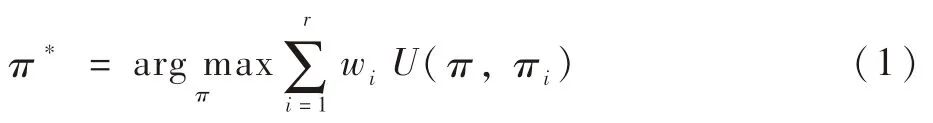
式中:U为衡量π和πi相似度的效用函数;wi为基础聚类πi的权重。
BV-RSA模型解决式(1)组合优化问题的流程框架如图1所示。

图1 BV-RSA模型框架Fig.1 Framework of BV-RSA model
其基本思想是:以经典模拟退火算法为基础,引入超点运动和投票箱机制来约束节点运动模式,以加快退火过程中近似最优解搜索。超点运动机制将基础聚类中获得完全一致性划分的若干数据样本定义为一个超点,并用超点取代其代表的样本子集参与退火过程,从而控制它们保持退火运动一致性,以加速节点聚簇行为。投票箱机制利用基础聚类对样本划分的部分一致性,为超点构造投票箱,超点运动方向受投票箱约束,以适当降低其标签变更的随机性,从而加快退火过程。
在式(1)的优化问题中,BV-RSA模型对U没有特殊要求,任何聚类评价的外部指标都可作为模型的效用函数。与文献[15]一样,本文采用聚类比较的Rand Index作为效用函数,其计算式为
式中:ni为组合聚类第i个簇包含的样本数量;为基础聚类πq的第j个簇包含的样本数量;为组合聚类第i个簇与πq的第j个簇包含的公共样本数量。
2 超点和投票箱机制
2.1 超点和超点运动
通常,有相当数量的数据样本在基础聚类中获得了一致性划分,这为组合聚类提供了先验信息。特别地,若2个数据样本在所有基础聚类中总是被划分到同一簇中,则其具有must-link特性。must-link特性具有传递性,由此形成超点。

表1给出了12个数据样本的3次基础聚类结果及其超点划分示例。
由超点定义可知,超点内部的数据样本在所有基础聚类中具有一致的簇标签,在组合聚类中也应被分配到同一个簇。BV-RSA模型用超点取代其内部数据样本参与退火过程,在降低样本数量的同时,保障了超点内部各样本的簇标签始终保持一致,称之为超点运动机制。
定义2不属于任何超点的数据样本被看作是特殊超点,称之为平凡超点;而包含多个数据样本的超点称为非平凡超点。
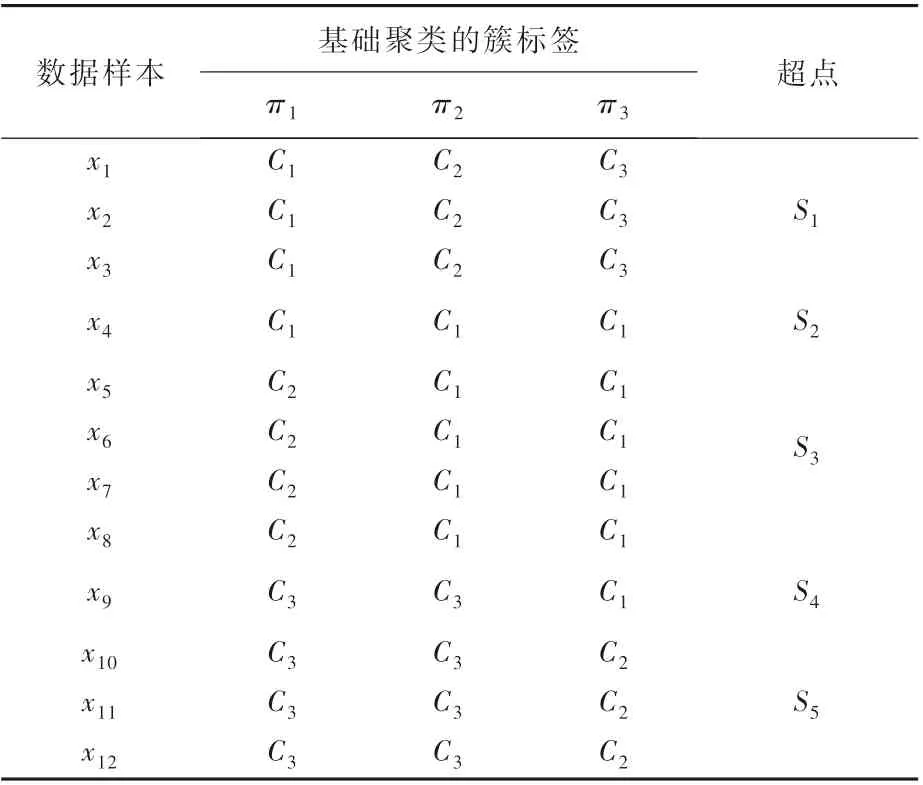
表1 基础聚类与超点示例Tab le 1 An exam p le of basic partition and super-objects
显然,非平凡超点的基数大于1,平凡超点的基数等于1。由此,将模拟退火的运动主体统一为超点,基础聚类矩阵Zn×r在去掉重复行后转化为超点基础聚类矩阵Ym×r。其中,m为平凡超点和非平凡超点的总数。
超点影响力与其基数正相关,因此退火过程的每次迭代将按超点基数的降序处理每个超点。由此,非平凡超点总是先于平凡超点被处理。
2.2 投票箱与标签选择
在经典模拟退火算法中,节点运动方向是随机选择的。对于组合聚类问题,这意味着随机变换数据样本的簇标签,然后判断该变更能否通过退火检验。随机标签选择使退火过程难于控制:检验阈值设置得高,则算法常结束于局部最优解,聚类质量低;检验阈值设置得低,目标函数可能在原地反复摇摆,算法收敛缓慢。BV-RSA模型基于基础聚类对样本划分的部分一致性,采用投票箱和随机选择融合的方法确定超点运动方向。
定义3已知超点基础聚类矩阵Ym×r=[y1,y2,…,ym]T,设yu和yv为与超点Su和Sv对应的矩阵行向量,则
在BV-RSA模型的退火过程中,当前运动节点(设为超点Su)的标签选择策略是:从Su的投票箱Bu中随机选出一个节点Sv,将Sv在组合聚类当前状态下的簇标签作为Su拟变更的新标签。该策略将基础聚类对样本划分的部分一致性作为约束节点运动方向的先验信息,同时保留了一定程度的算法随机性。
3 BV-RSA模型的算法实现
3.1 算法描述
BV-RSA模型的具体实现算法描述如下,包括初始化和迭代退火2个子过程。
1)初始化过程
步骤1计算超点集合SS={S1,S2,…,Sm},并按超点基数进行排序。
步骤2对每个Su∈SS(u=1,2,…,m),计算其投票箱Bu。
步骤3删除Zn×r的重复行,获得超点基础聚类矩阵Ym×r。
步骤4按特定策略,初始化每个超点的簇标签,形成π的初值。
步骤5设置退火过程控制参数,包括:初始温度T、温度冷却比C、变更接受阈值P0。
2)迭代退火过程
步骤1对每个超点Su∈SS(u=1,2,…,m),执行如下操作:①提取Su在π中的簇标签(设为i),即Lπ(Su)=i;②从Su的投票箱Bu中随机选出具有投票权的一个超点(设为Sv),提取Sv在π中的簇标签(设为i′),即Lπ(Sv)=i′;③计算超点Su标签由i变为i′引起的目标函数值变化,若P(π(Su):Lπ(Su)→i′)>P0,则接受Su标签变更,令Lπ(Su)=i′。
步骤2 若符合迭代结束条件,则算法结束;否则,令T=T×C,重复退火过程的步骤1。
初始化过程主要完成3项工作:①计算超点集、超点投票箱和超点基础划分矩阵;②为退火过程设置控制参数;③按指定策略生成组合聚类的初始划分,例如:为每个超点随机分配簇标签(R策略),或随机选择一个基础聚类(矩阵Ym×r的某一列)作为初始状态(C策略)。
退火过程以迭代方式进行,通过不断改变超点簇标签,逐渐逼近组合聚类的近似最优解。每次迭代过程分2个阶段进行:第1阶段,对所有非平凡超点进行标签选择和变更检验,处理顺序按超点基数由大到小依次进行;第2阶段,处理所有平凡超点。当目标函数值不再发生变化或达到指定迭代次数时,退火过程结束。
3.2 退火检验的增量计算

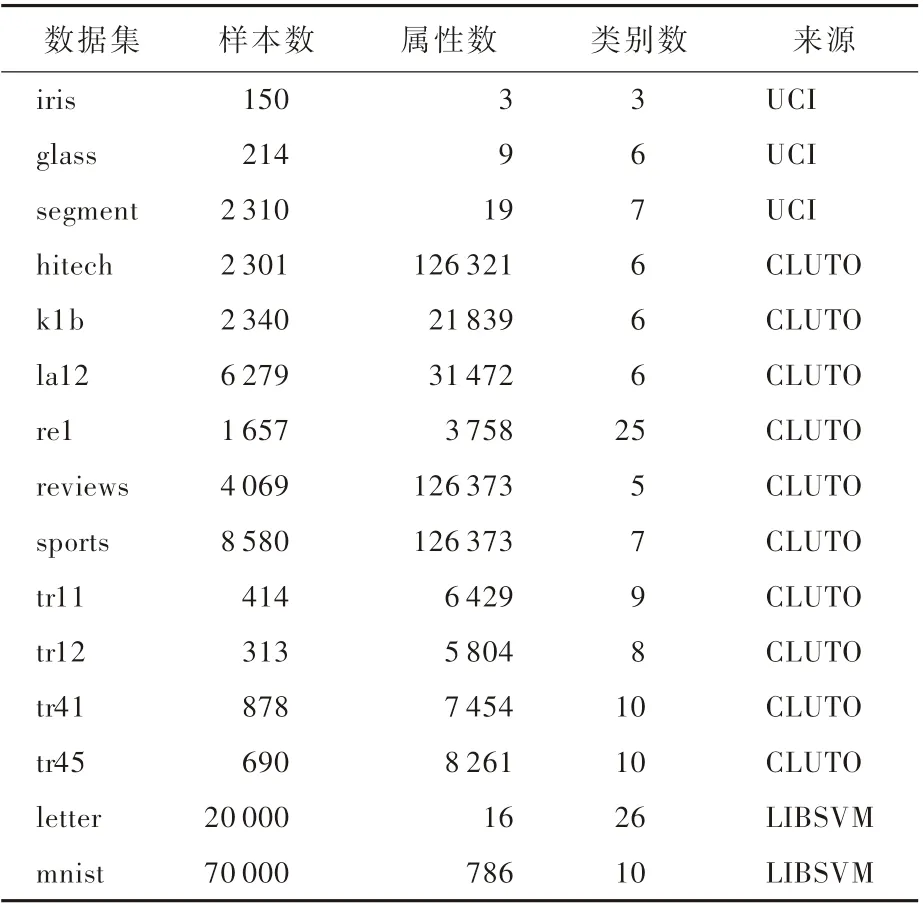
表2 实验数据集描述Table 2 Description of experim ental datasets

由式(6)和式(7)可导出h1和的更新计算方法如式(8)和式(9)所示。而只与基础聚类相关,在退火检验时不需要重新计算。
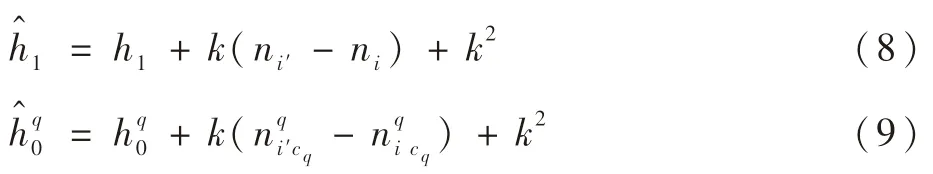
由式(2)、式(8)和式(9),可增量计算超点Su标签变化引起的目标函数值变化。设Δτ为标签变更前后的目标函数值差额,T为当前退火温度,若式(10)给出的P值大于检验阈值P0,则接受Su的标签变更。
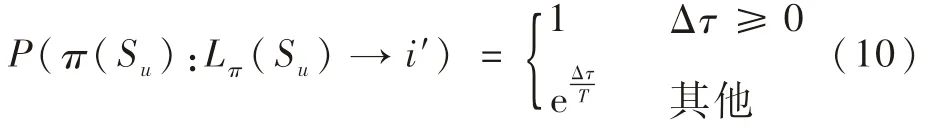
4 实验分析及模型应用
4.1 数据集和实验设置
本文选用如表2所示的15个公开数据集来检验BV-RSA模型的有效性。
针对每个数据集,采用k-means算法生成50个基础聚类,它们在组合聚类目标函数中采用均等权重,即wi=0.02(i=1,2,…,50)。模拟退火的初始状态分别由R策略和C策略产生。除初始状态外,其他控制参数分别为:标签变更检验阈值P0=0.8,初始温度T=0.05,温度冷却比C=0.9。针对每个数据集,BV-RSA 模型运行10次并取精度均值,分别与 CSPA、HGPA、MCLA[3]进行比较。
4.2 实验结果分析
表3给出了BV-RSA模型与基准算法的精度比较。在全部15个数据集中,BV-RSA模型在10个数据集上获得了最优结果。CSPA算法在glass和reviews和tr12数据集结果最优,但在有些数据集上效果不理想,特别是mnist数据集样本点较多,CSPA算法没有输出结果。这是因为CSPA算法对每个基础聚类都需要计算一次相似度矩阵,在基础聚类数量多、数据集规模大时,算法计算压力和内存开销过高,较难适应大数据集上的组合聚类任务。比较而言,MCLA 算法与BV-RSA模型的结果相近,但BV-RSA模型在大数据集letter和mnist上的表现更好一些。
在鲁棒性方面,图2给出了k1b数据集在不同基础聚类数量的情况下,各模型的组合聚类准确率的波动情况。从图2中可以看出:BV-RSA模型的C策略(BV-RSA/C)、BV-RSA模型的R策略(BV-RSA/R)和CSPA模型面对不同数量的基础聚类时,表现出了相对稳定的模型精度;而模型MCLA和HGPA则有一定程度的准确率波动。

表3 各模型聚类结果的精度比较Tab le 3 Com parison of clustering resu lt precision of d ifferen tm odels
4.3 网约车司机分群应用
本文利用BV-RSA模型对某网约车平台的司机脱敏数据进行了分群应用,以帮助该平台强化司机细分管理,并在约车高峰时段辅助提高运力调度的有效性。
本文采集了100 000条约车平司机信息及其2017年4月的接单数据作为模型输入,输入数据的具体格式如表4所示。k-means和BV-RSA组合聚类将网约车司机划分为4个群体,各群体人数如图3所示。
同时分析了各群体司机在不同时段的接单量分布。图4和图5分别给出了各类司机群体在工作日和周末的接单量分布,可以看出:与k-means方法相比,BV-RSA模型得到的各类司机群体,其群体内部的接单量差异更小,表现出更好的内聚性。同样地,本文分析了各类司机群体在早高峰、晚高峰和常规时段的接单量分布,获得了类似的分析结论,限于篇幅关系,不再一一赘述。

图2 基础聚类数量对模型精度的影响Fig.2 Impact of number of basic clusters on model precision

表4 输入数据描述Tab le 4 Descrip tion of input data
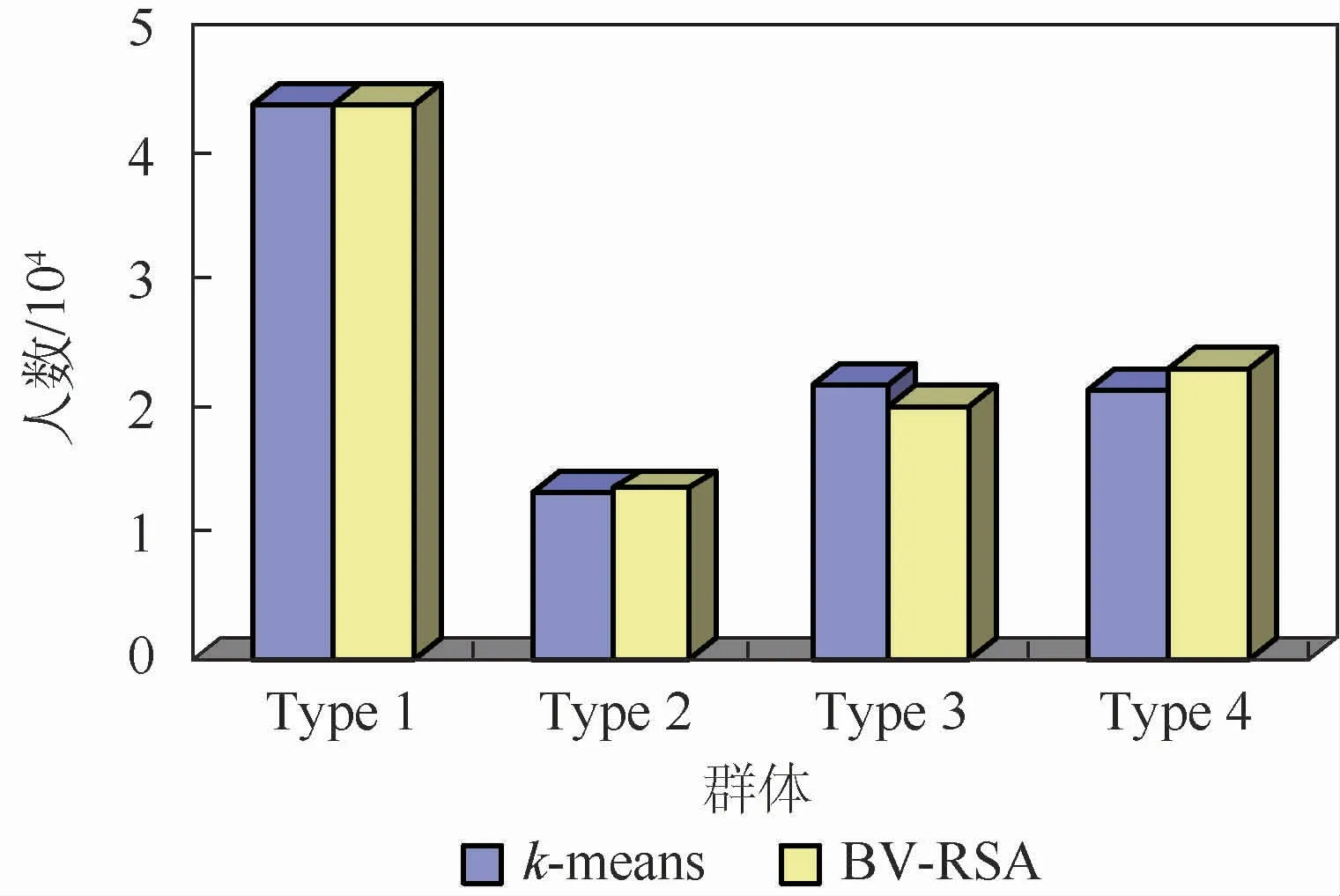
图3 k-means和BV-RSA模型的司机分群结果Fig.3 Driver grouping result obtained from k-means and BV-RSA model
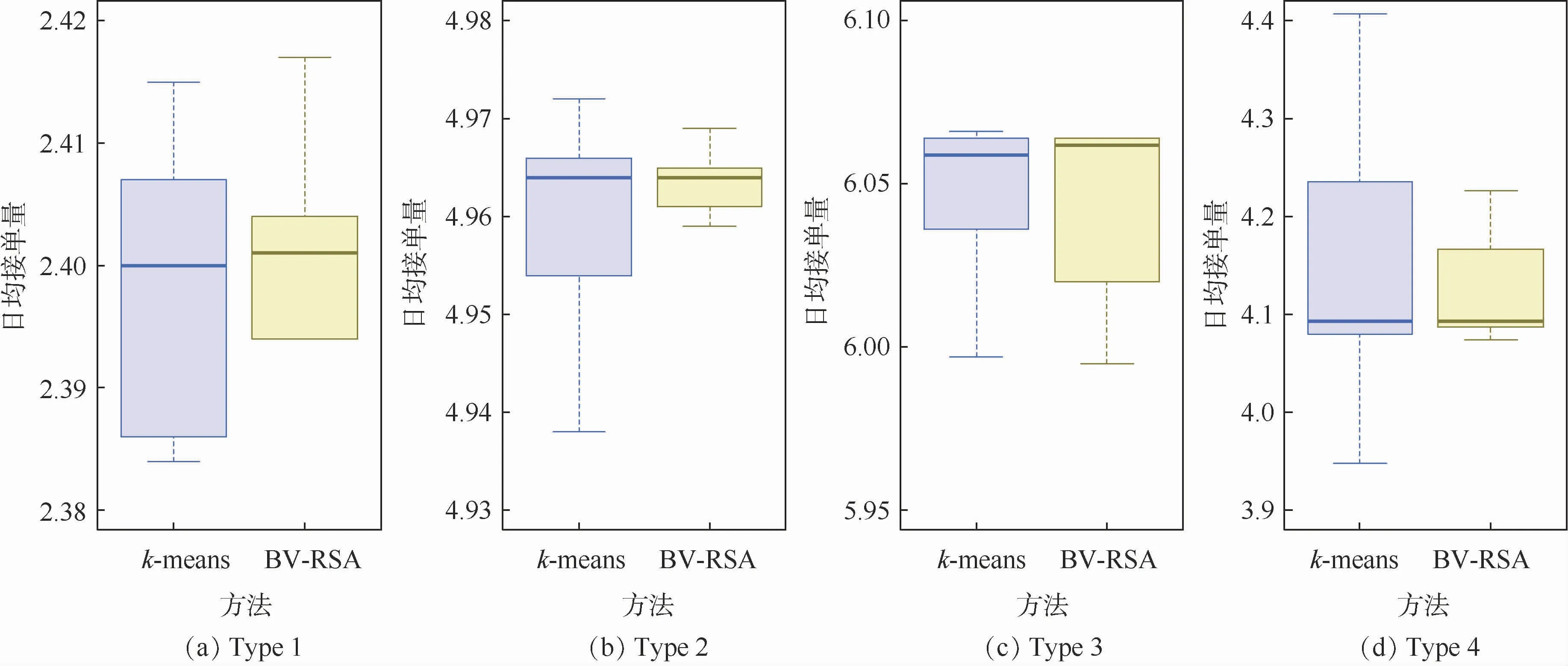
图5 各类司机群体的周末接单量分布Fig.5 Distribution of order quantity received by different driver groups on weekend
5 结 论
本文提出了BV-RSA模型,该模型的主要贡献包括:
1)引入了超点运动机制,使满足完全一致性划分条件的若干数据样本以成组方式参与退火过程,在压缩样本空间的同时,加快了节点聚类速度。
2)对于每个超点,根据基础划分的部分一致性构造其投票箱,超点运动的随机性受投票箱约束。该机制保留了解空间搜索的部分随机性,同时引入启发信息加快模拟退火过程的收敛。
3)BV-RSA模型采用与文献[15]同样的效用函数,推导了超点运动引起效用函数变化的增量计算方法,降低了模拟退火检验的计算开销。
15个标准数据集上的实验表明,BV-RSA模型在10个数据集上获得了最优结果,且模型精度对基础聚类数量的变化不敏感,表现出良好的鲁棒性。
在后续研究中,将进一步设计BV-RSA模型的并行计算方案,拓宽其在大数据集上的应用。
