静电传感器测量固体颗粒质量流量实验研究

吴诗彤，闫勇，2，钱相臣，*

（1.华北电力大学 控制与计算机工程学院，北京102206； 2.肯特大学 工程与数字艺术学院，肯特CT2 7NT）

在高温高压等极端条件下，航空发动机气路中的机械部件容易磨损并发生故障，对气路中的固体颗粒质量流量进行实时监测，有助于获得气路部件的状态信息［1-3］。此外，航空发动机排放物中固体颗粒含量反映了发动机内燃料的成分及其燃烧情况，检测颗粒物生成量对监控发动机工作性能提供重要的信息。一部分航空发动机气路和尾气排放管路使用的是非圆心对称的方形截面管道，如美军F-22战斗机使用的二元矢量推力喷口，因为存在4个直角，其中固体颗粒流动状态比圆形管道更加复杂，因此固体颗粒质量流量的准确测量是学术界和工业界公认的难题。

现有的气固两相流固相质量流量测量方法在测量原理方面有局限性。如热传导法需要较长的响应时间，不适用于需要快速响应的工业过程［4］；数字图像法测量时，微小颗粒易吸附在观测窗口上造成污损；射线法测量装置体积大，价格昂贵，维护困难［4］。静电传感器结构简单、鲁棒性好、成本低廉，适用于恶劣的环境［5］，在检测航空发动机系统中的固体颗粒参数和故障预警等方面具有突出的应用前景［6-8］。已有的研究多数用于圆形截面气力输送管道中的气固两相流固相浓度和速度的测量，如环形电极、弧形电极、棒状电极和侵入式阵列［4，9-10］，而用于方形气力输送管道质量流量测量的静电传感器的研究较少。Murnane等［11］首次提出了适用于方形截面管道的方环形电极结构物理模型。Peng等［12］建立了方环形电极的数学模型，并通过理论计算和实验测试研究了电极灵敏度分布、频率响应等感应特性。Jurjevˇciˇc等［13］提出了适用于磨煤机出口处大直径矩形管道的侵入式和分布式棒状电极的物理模型。Zhang等［14］设计了由12对均匀嵌入在4个管壁上的条状电极组成的非侵入式条状静电传感器阵列，并进行了实验测试。

航空发动机气路或者排放物中的颗粒浓度和速度是在应用中普遍关注的基本参数。本文基于静电传感器测量的固体颗粒浓度和速度2个参数获得固体颗粒的质量流量，并对质量流量的准确性进行了研究。实验中，使用方环形、非侵入式条状和侵入式条状3种不同形式的静电传感器对方形管道中固体颗粒质量流量进行同步测量，并根据给定质量流量分别对3种静电传感器测量的数据进行全工况标定，对比分析其测量准确性。

1 测量原理

1.1 测量系统

固体颗粒物在气体曳力驱动下的运动过程中，由于颗粒与颗粒、颗粒与管壁、颗粒与空气之间的摩擦和碰撞，其表面会产生一定量的静电电荷。运动的带电颗粒产生时变静电场，使静电传感器感应出微弱的静电信号。如图1所示，静电传感器阵列测量得到的微弱静电信号在信号调理单元中被转换为电压信号，并进行信号放大和滤波。利用数据采集卡对滤波后的信号进行采样，利用数字信号处理得到固体颗粒动态参数。固体颗粒运动速度通过互相关测速法获得，通过计算上游和下游2个静电传感器测量信号的互相关函数，可以获得固体颗粒流经2个静电传感器的时间差τm，由于上、下游静电传感器间距L已知，固体颗粒速度v计算式为［5，15］测量信号的均方根值ARMS可以用于表征固体颗粒的相对浓度［5，15］，计算公式为

式中：sn为采样得到的静电信号；N为采样值数量。根据固体颗粒的速度和相对浓度，即可计算得到其质量流量［15］。

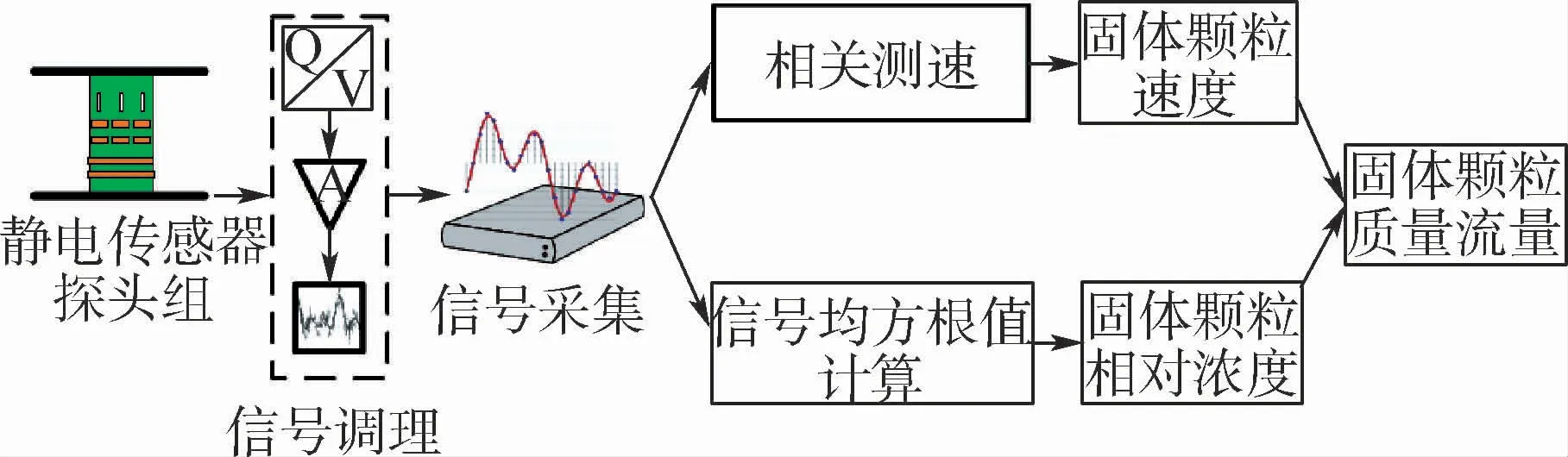
图1 静电传感器测量系统结构示意图Fig.1 Schematic diagram of principles of electrostatic sensor measurement system

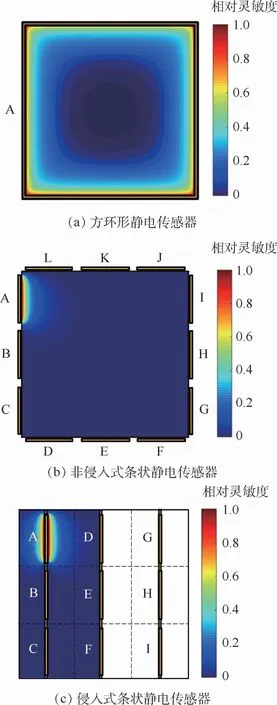
图2 静电传感器电极布置及其空间相对灵敏度分布Fig.2 Electrode layout and space relative sensitivity distribution of electrostatic sensor

图2为组成静电传感器探头的3种静电传感器电极的空间相对灵敏度分布。方环形静电传感器由一对方环形电极构成，具有结构简单的优势，其 敏感区域覆盖整个管道截面［8，12］。非侵入式条状静电传感器由12对均匀嵌入在4个管壁上的电极构成，可以测量被测区域中局部范围内固体颗粒的动态参数［14，16］。从图2（a）、（b）中可以看出，由于这2种静电传感器都采用非侵入式设计，因而存在灵敏场分布不均匀的问题。侵入式条状静电传感器所包含的9对电极均匀布置在方形管道中，可以测量局部区域固体颗粒的动态参数，但是因采用侵入式设计，会对流场产生影响，且电极容易受到固体颗粒的磨损，不适合在线长期测量，更适用于标定非侵入式条状静电传感器。

1.2 固体颗粒截面平均速度和浓度测量

将2个结构完全相同的静电传感器平行布置，通过测量被测区域内固体颗粒产生的静电信号，即可获得固体颗粒的流动速度和浓度。表1为方环形静电传感器Ⅰ、非侵入式条状静电传感器Ⅱ和侵入式条状静电传感器Ⅲ计算固体颗粒截面平均速度va和截面平均信号均方根值ARMS，a的公式。

表1 三种静电传感器截面平均参数计算Tab le 1 C ross-sectional average param eter calcu lation using three types of electrostatic sensors

通过静电传感器Ⅱ，可分别得到12个局部速度（vA，vB，…，vL）和信号均方根值（ARMS，A，ARMS，B，…，ARMS，L）。局部速度值的算术平均值即为截面平均速度，局部信号均方根值之和即为截面平均信号均方根值。对于静电传感器Ⅲ，根据电极敏感区域分布，将测量截面平均为9个区域，可分别得到9个局部速度（vA，vB，…，vI）和信号均方根值（ARMS，A，ARMS，B，…，ARMS，I），截面平均参数计算方法与静电传感器Ⅱ相同。

1.3 固体颗粒质量流量计算

根据固体颗粒的截面平均速度和信号均方根值，可以计算固体颗粒质量流量qm（t）［15］为

式中：S为管道截面积；ρs为颗粒密度；βa为截面颗粒平均浓度；K、b为常数，系数K利用给定的质量流量、截面平均速度、截面平均信号均方根值标定得到。

2 静电传感器与实验装置

图3 静电传感器探头结构与尺寸Fig.3 Structure and dimension of electrostatic sensor head

用于测量固体颗粒质量流量的静电传感器探头如图3所示。沿固体颗粒流动方向，依次为静电传感器Ⅰ、静电传感器Ⅱ和静电传感器Ⅲ，其中所有电极的轴向宽度均为3mm，每个电极对中2个电极的中心间距均为15mm。方形截面管道气力输送实验装置如图4所示。实验装置主要由给料系统、方形气力输送管路、粉料回收系统及负压发生系统构成。粉体质量流量通过调节给料机给料量进行控制，固体颗粒运动速度通过调节负压发生系统的工作电压控制管路中的输送风速实现。实验平台水平总长度为5 100mm，垂直高度为2 200mm，管道内壁边长为54mm，静电传感器探头组被安装于右侧垂直管段距下方水平管段1 200mm处。

图4 方形截面管道气力输送实验装置Fig.4 Pneumatic conveying experimental facility with square-shaped pipeline

3 实验结果与分析

3.1 实验条件

如表2所示，实验在4种输送气流速度和4种给料机给定固体颗粒质量流量组合成的16种不同工况下进行。气流速度范围为19～31m／s，利用热线风速仪在管道横截面中心处测量得到。固体颗粒使用平均粒径为61.8μm 的精细面粉（由OMEC-LOP9激光粒径分析仪测量），质量流量范围为0.56～2.22 g／s，折合固相体积浓度范围为0.001 2% ～0.007 7%。实验过程中，工况稳定后在采样频率25 kHz条件下连续采集静电信号10 s，重复测试2组。其中，第1组实验数据用于标定式（3）中的系数K，依据已有文献［15］，系数b设 定 为－0.5［17］。第2组 实 验 数 据 用 于 验 证固体颗粒质量流量。每2 000个静电信号采样数据用于计算固体颗粒速度值和相对浓度（用信号均方根幅值表征），单次实验可得到125个固体颗粒速度值和相对浓度值。实验室温为26℃，相对湿度约70%，PM2.5浓度为67μg／m3。

表2 实验条件Table 2 Experim ental condition

3.2 原始静电信号测量

固体颗粒质量流量为1.11 g／s（M2）时，静电传感器Ⅰ、静电传感器Ⅱ中的电极K、静电传感器Ⅲ中的电极D在不同输送气流速度条件下测得的静电信号如图5所示。显然，静电传感器Ⅰ的测量信号的幅值最大，静电传感器Ⅱ和静电传感器Ⅲ的信号幅值相近。这是因为原始信号的幅值主要受到电极尺寸的影响，静电传感器Ⅰ的电极尺寸最大，而静电传感器Ⅱ和静电传感器Ⅲ具有相同的电极尺寸且较小。另外，对比不同电极的面积可以进一步发现，方环形电极的面积是条状电极的14.4倍，但是测量信号的波动幅度却仅有约3.2倍，这是由静电传感器的感应原理和空间滤波效应决定的［14］。由图5可以看出，原始信号的幅值随着输送气流速度的增大略微下降。

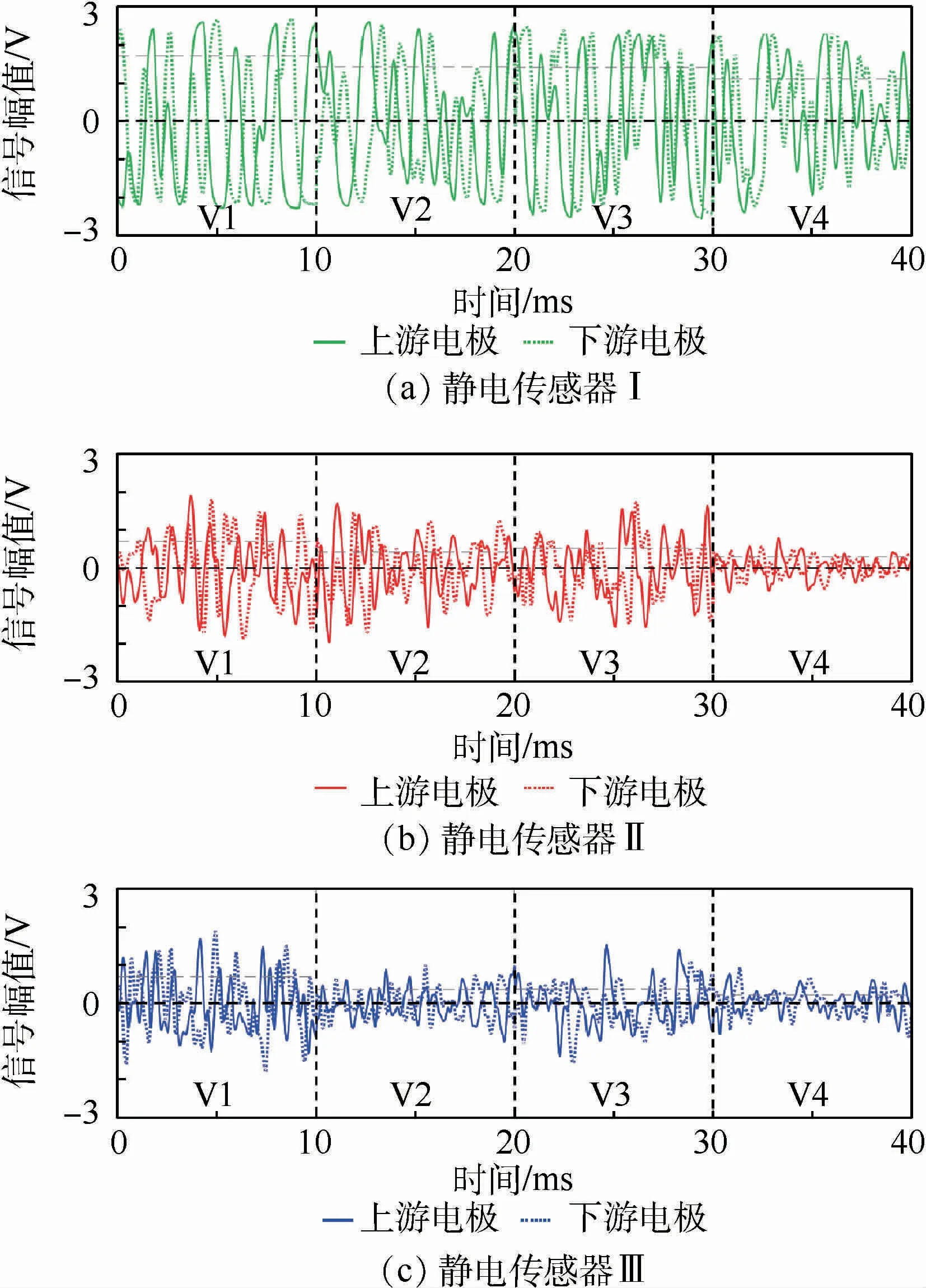
图5 不同输送气流速度条件下测得的原始静电信号Fig.5 Raw electrostatic signalmeasured under different conveying gas velocities

3.3 管道截面平均浓度和速度

各静电传感器所有电极的信号均方根值之和即为各静电传感器截面平均信号均方根值（见表1）。固体颗粒质量流量为1.11 g／s（M2）时，静电传感器Ⅰ、静电传感器Ⅱ、静电传感器Ⅲ在不同输送气流速度条件下测得的静电信号均方根幅值如图6所示。可以看出，每一静电传感器的信号均方根值随着输送气流速度的增大而略微下降，当输送气流速度增大4m／s时，静电传感器Ⅰ、静电传感器Ⅱ和静电传感器Ⅲ的信号均方根值平均减小0.4%、0.9%和0.7%，因固体颗粒质量流量一定时，管道中固体颗粒的浓度伴随着速度增大而略微降低。由于空间滤波效应，静电传感器Ⅰ的信号均方根值的波动幅度、均值及随输送气流速度变化的趋势最小，因此不能反映固体颗粒浓度的瞬时变化。

利用静电传感器Ⅰ、静电传感器Ⅱ和静电传感器Ⅲ测量的固体颗粒管道截面平均速度如图7所示，同一工况下固体颗粒速度测量值波动较平稳。因为固体颗粒在管道截面呈现中心区域颗粒速度高、四周区域颗粒速度低的分布，对管道内部区域固体颗粒较敏感的静电传感器Ⅲ测量的固体颗粒速度平均比对靠近管壁区域固体颗粒较敏感的静电传感器Ⅰ和静电传感器Ⅱ的测量值分别高1.8m／s和3.6m／s。

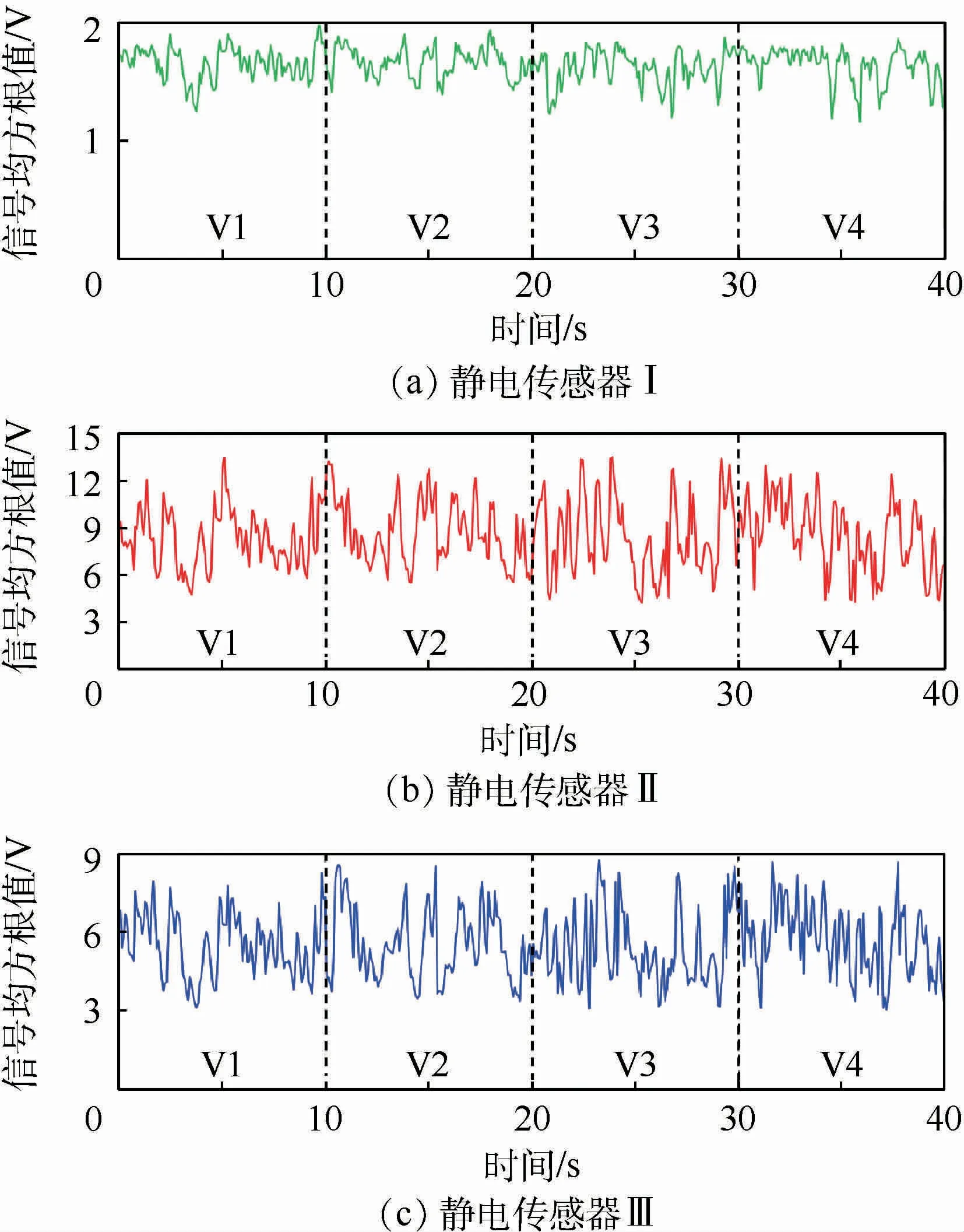
图6 不同输送气流速度条件下测得的信号均方根值Fig.6 Root-mean-square value of signalsmeasured under different conveying gas velocities

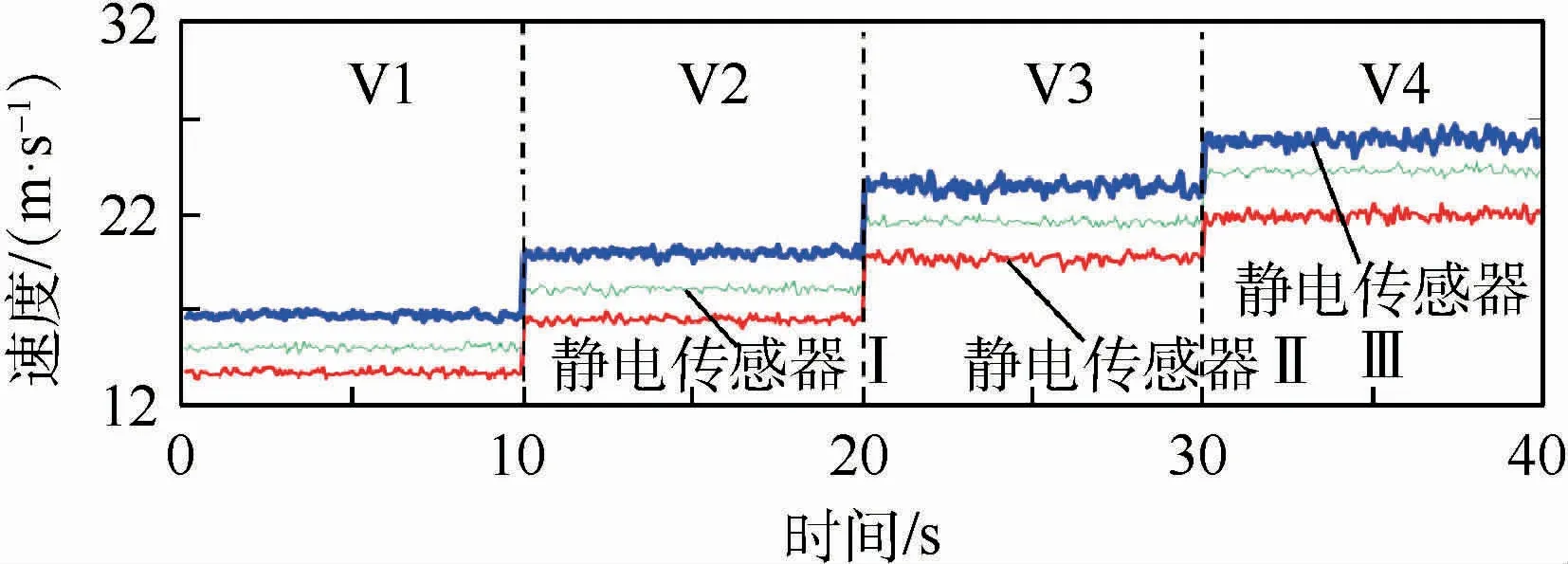
图7 不同输送气流速度条件下固体颗粒的速度Fig.7 Velocity of solid particlesmeasured under different conveying gas velocities

3.4 单一工况

根据静电传感器测量的固体颗粒相对浓度和速度，以及实验中给料机设定的给料量可以标定系数K。针对不同气流速度、相同固体颗粒质量流量条件下，各静电传感器第1次实验数据得到的速度值、信号均方根值和给定质量流量，根据式（3）拟合得到系数K值，如图8所示。将拟合获得的系数K代入式（3），利用第2组实验数据得到的固体颗粒质量流量及相对误差如图9所示。可以发现，利用静电传感器Ⅰ的测量信号进行标定的相对误差最小，测量可靠性最好。在实际工业测量中，由于无法针对全部工况进行标定，因此需要根据有限工况数据标定得到一个可以适用于所有工况的、折中的系数K。

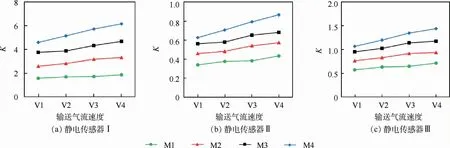
图8 单一工况标定得到的系数KFig.8 Coefficient K obtained by individual test condition calibration

图9 单一工况标定得到的固体颗粒质量流量测量值与相对误差Fig.9 Measured mass flow and relative error obtained by individual test condition calibration

3.5 全工况

对图8中各静电传感器在全部16个实验条件下标定获得的系数K进行拟合，使拟合得到的K值与原16个K值的差值的平方和最小，分别得到3种静电传感器的K值：KⅠ＝3.61，KⅡ＝0.56，KⅢ＝0.95。将KⅠ、KⅡ和KⅢ分别代入式（3），利用第2组实验数据得到了3种静电传感器测量的固体颗粒质量流量及其与真实固体颗粒质量流量的相对误差，分别如图10和图11所示。与图9相比，全工况标定得到的固体颗粒质量流量与给定值偏差较大。在图11中，针对各静电传感器的相对误差拟合出一个平面，使16个误差点到该平面距离和最小，得到平面Ⅰ、平面Ⅱ和平面Ⅲ。

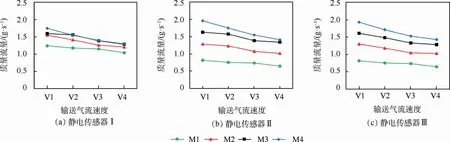
图10 全工况标定得到的固体颗粒质量流量Fig.10 Mass flow of solid particle obtained by all-test-condition calibration

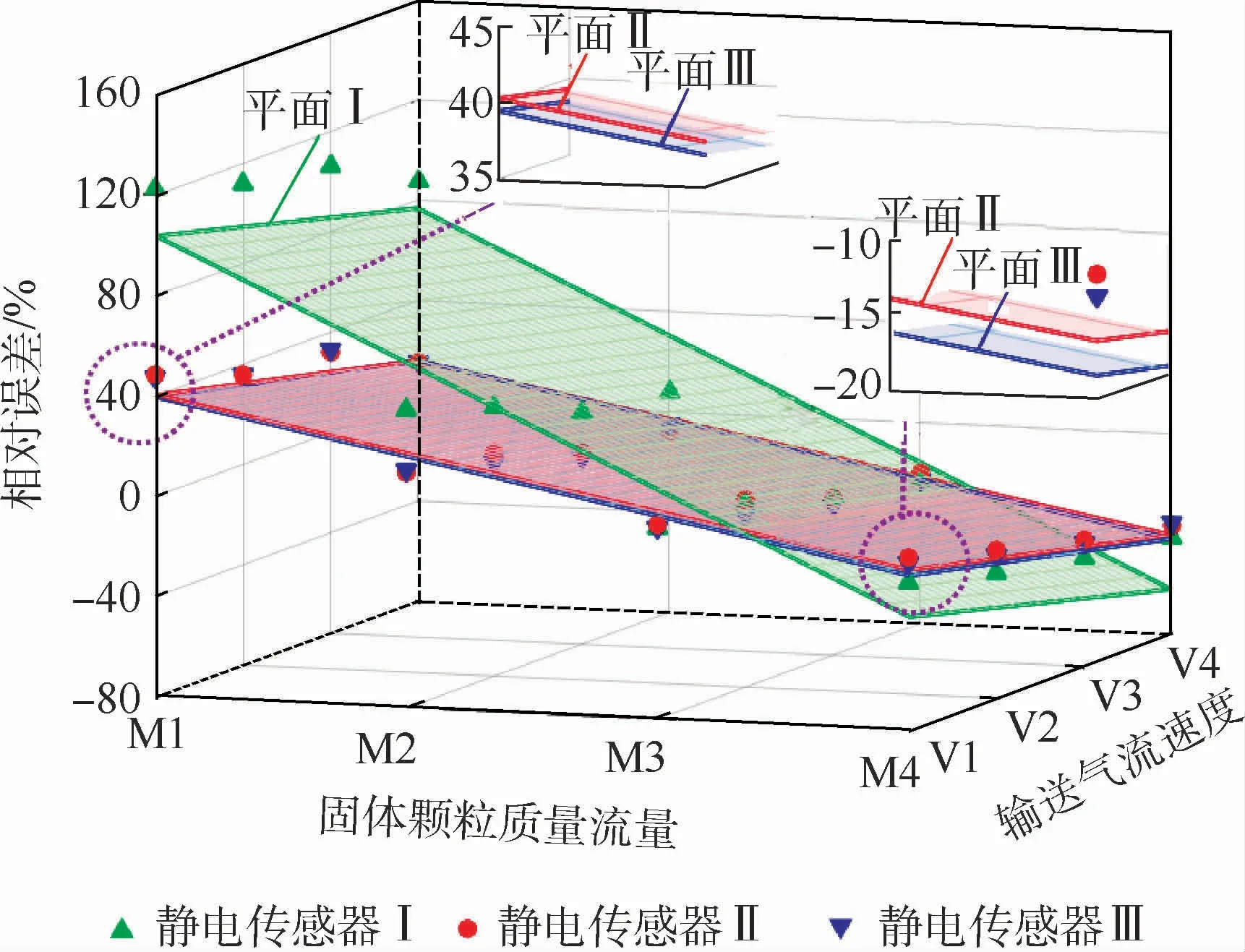
图11 全工况标定得到的固体颗粒质量流量的相对误差Fig.11 Relative error ofmass flow measurement of solid particles obtained from all-test-condition calibration

如图11所示，平面Ⅰ的倾斜度和极值最大，即测量值和真实值的相对误差最大。平面Ⅱ和平面Ⅲ的平均高度相似，在固体颗粒质量流量较低（工况M1、M2）时，静电传感器Ⅲ的相对误差较低，测量值更接近真实值；在固体颗粒质量流量较高（工况M3、M4）时，静电传感器Ⅱ的相对误差较低，测量误差较低。

4 结 论

本文利用3种静电传感器测量方形截面气力输送管道中稀相固体颗粒的质量流量，并针对16种实验工况标定了固体颗粒质量流量，实验结果的对比分析表明：

1）利用方环形静电电极测量质量流量的测量准确度最低。

2）在质量流量较低时，利用侵入式条状静电电极阵列测量质量流量的准确度最高。

3）在质量流量较高时，利用非侵入式条状静电电极阵列测量质量流量的准确度最高。

而针对单一工况标定质量流量时，利用方环形静电电极测量质量流量的测量准确度最高，利用侵入式条状静电电极阵列测量质量流量的准确度最低。