电容成像双共轭梯度图像重建改进算法

马敏，范广永，孙颖

（中国民航大学 电子信息与自动化学院，天津300300）

航空发动机作为航空器的核心设备，其系统的结构复杂且长期工作于高温、高压的恶劣环境下，限制了一些传统设备对航空发动机尾气进行监测，基于电容层析成像技术（Electrical Capacitance Tomography，ECT）的航空发动机尾气检测系统为解决此问题提供了可能性。

ECT技术的优点在于非侵入性、安全性、响应速度快、安装便捷及成本低等，使得其在工业过程可视化检测中成为一项极具发展潜力的技术［1］。

1984年，Brown对电学成像技术进行了综述，并且提出了反投影算法［2］；1985年，Murai和Kagawa［3］根据Geselowitz灵敏度原理将灵敏度系数法引入到电学成像中；1998年，Vauhkonen等［4］提出了卡尔曼滤波法，并将其应用到电学层析成像中；1999年，杨五强等［5］提出了改进的Landweber迭代算法，并成功应用到电学成像领域；2002年，Kim等［6］研究出一种扩展的卡尔曼滤波算法；2003年，杨五强等［7］对ECT技术中常用的算法进行了综述；2005年，王化祥等［8］提出了基于灵敏度矩阵的奇异值分解理论及正则化共轭梯度（Conjugate Gradient，CG）法；2007年，王化祥等［9］提出了基于自适应网格的改进总变差算法。

本文将双共轭梯度（Biconjugate Gradient，BICG）算法引入到ECT技术中。为了得到更好的效果，对该算法做了一些改进，将BICG算法与正则化算法相结合，并与传统的迭代类算法进行比较［10-11］。

1 ECT系统

1.1 系统组成

传统的ECT系统主要由三大子系统组成：传感器系统、数据采集系统和上位机成像系统。3个系统具有各自的功能。传感器系统主要测量极板间的电容值，数据采集系统将测得的电容值传输到上位机，上位机通过软件及程序进行图像重建，这就是一个简单的ECT系统的成像过程。图1为传统ECT系统模型。

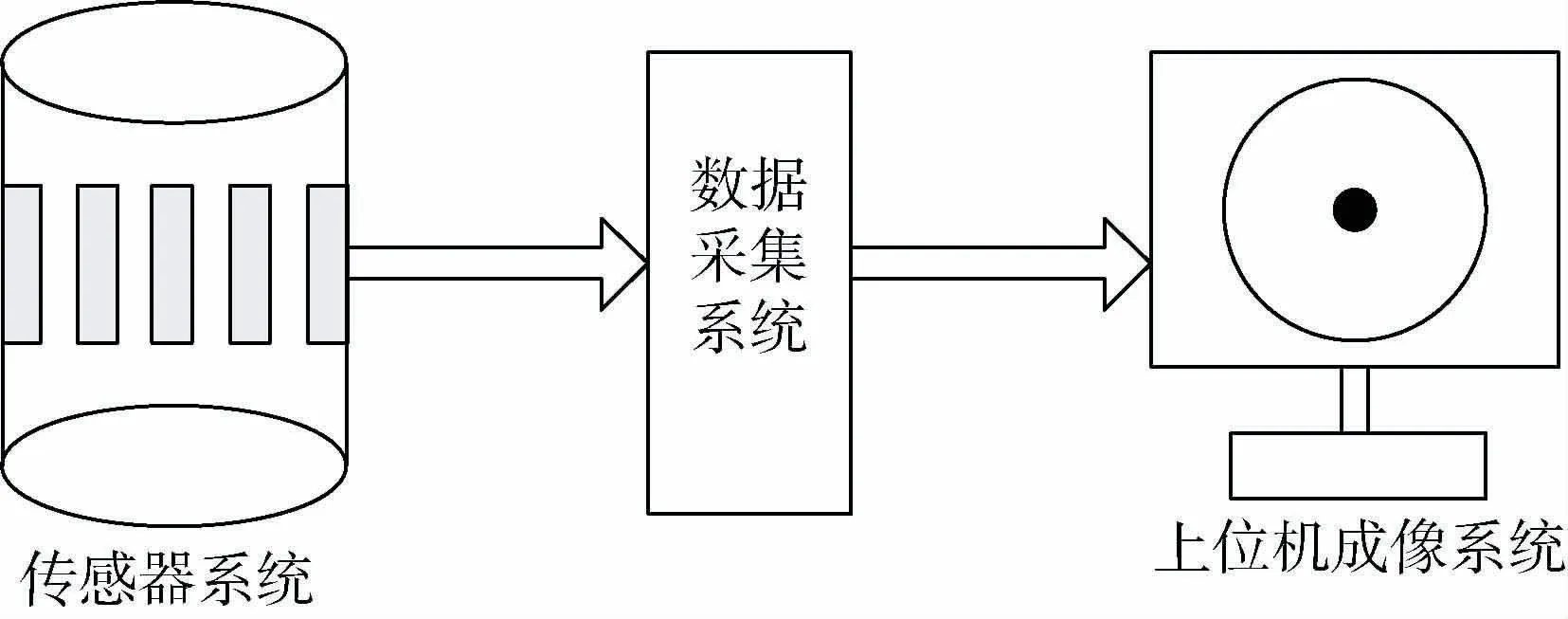
图1 传统ECT系统模型Fig.1 Traditional ECT system model

1.2 算法介绍

CG算法一般适用于求解大型线性方程，属于最速下降法的一种改进，误差不计的条件下，CG算法在N步内就可以达到收敛效果。虽然CG算法在有限的步骤内就可到达收敛，但对于求解出的矩阵G来说，N的取值是非常大的。因此，本文在经典CG算法的基础上引进了BICG算法来提高计算速度。BICG算法使用2组共扼向量作为搜索方向，而CG算法仅使用1组共轭向量作为搜索方向，因此BICG算法的速度得到大幅度提高。如果系数矩阵A为实对称阵，且求解节点数较多时，BICG算法收敛速度将会更快。通过实验仿真和数据对比，验证了BICG算法效果明显高于其他几种迭代类算法。图2为BICG算法的计算流程。

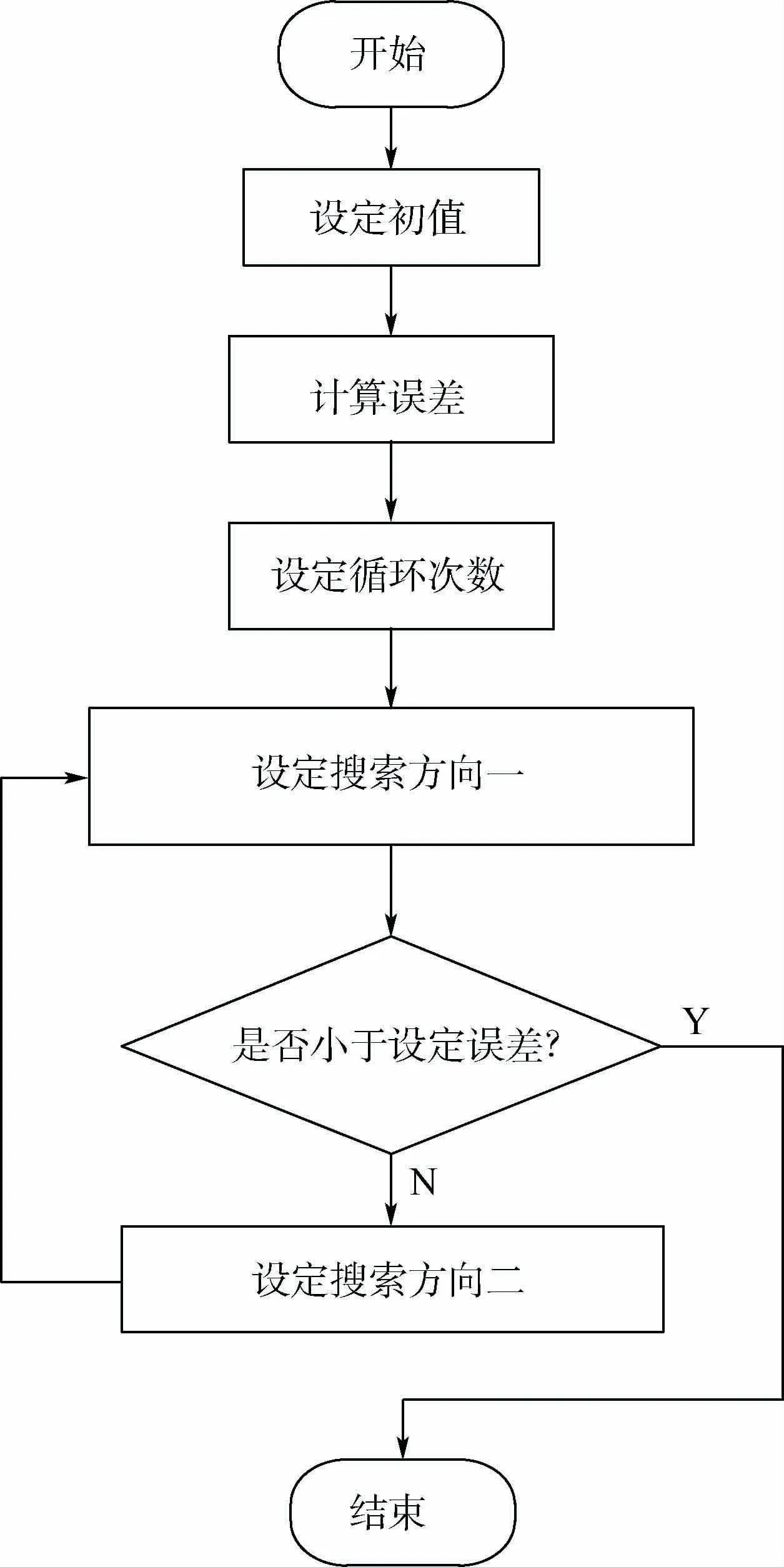
图2 BICG算法计算流程Fig.2 BICG algorithm calculation flowchart

2 仿真设计

仿真使用COMSOL5.3软件对12电极的ECT系统进行建模，对系统进行有限元分割，分割网络设置为64×64，共有3 228个有效单元，通过有效网络来求解场内的电容值及灵敏度分布情况，即ECT技术的正问题。空场材料的介电常数设为1，屏蔽罩及电极的介电常数为2.2，管道内被测物体的介电常数设为4.2。图3（a）为电极数目为12的传统ECT系统模型，图3（b）为通过有限元分割后得到的模型。

通过有限元方法分割完网格后，对场内进行计算，计算结果可通过静电场电势（见图4（a））及场内电场线分布情况（见图4（b））呈现出来。

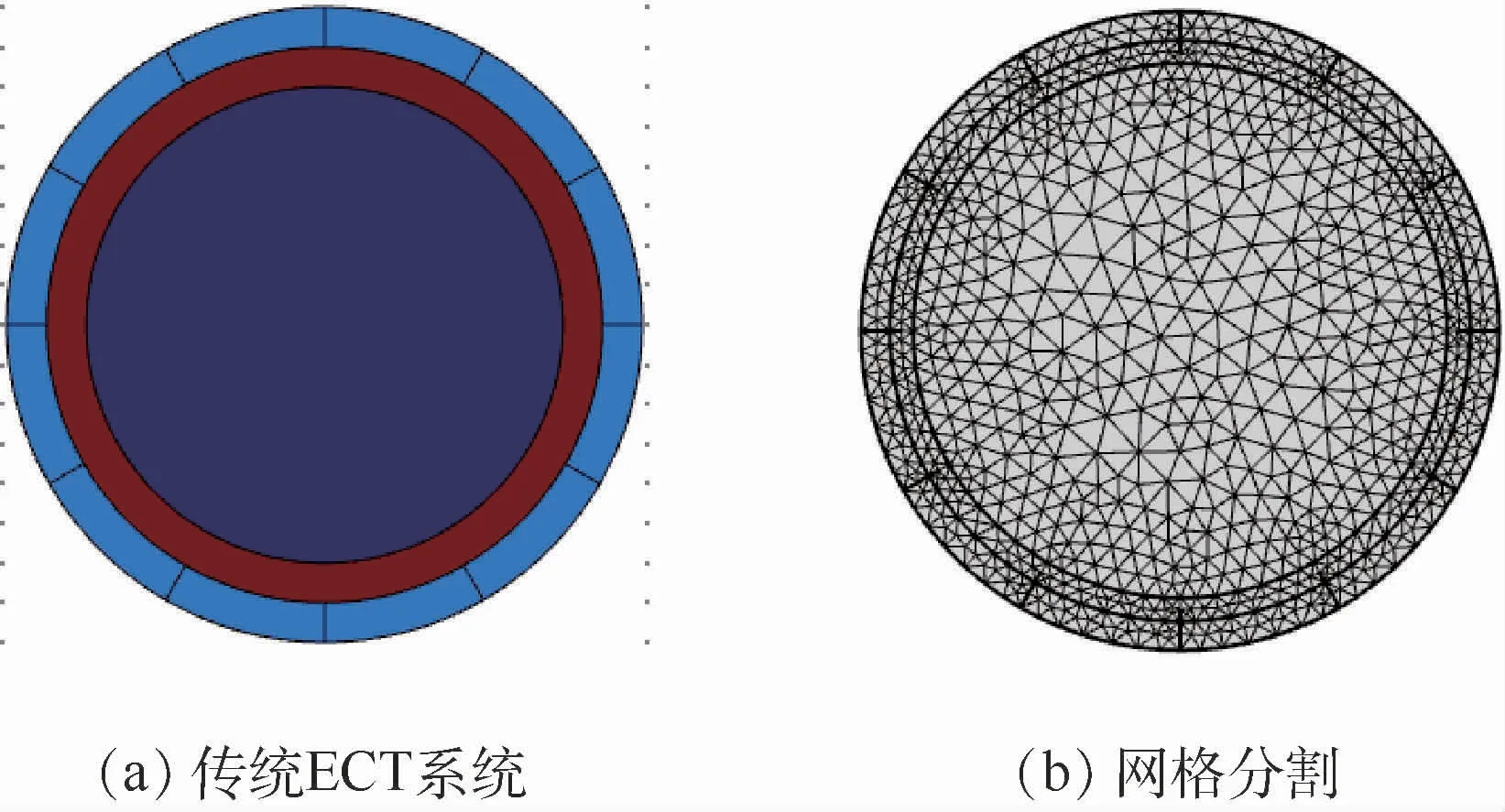
图3 ECT系统仿真Fig.3 ECT system simulation

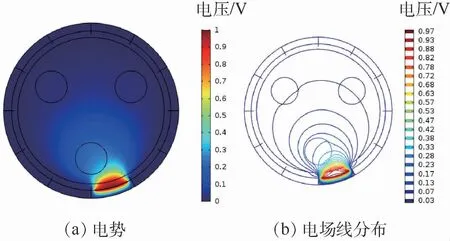
图4 传感器电势分布Fig.4 Sensor potential distribution

3 图像重建算法

实验通过5种图像重建算法，即Tikhonov算法、Landweber算法、CG算法、BICG算法及本文改进算法对各模型仿真进行图像重建［12-13］。

3.1 LBP算法

LBP算法基于以下2个理想条件：①灵敏度系数均匀分布在场内；②电容值与灵敏度矩阵和介质分布有关。

式中：c为电容值矩阵；s为灵敏度矩阵；g为介质分布向量；sT为s的转置矩阵，用来代替s的逆矩阵。

3.2 Landweber算法

Landweber算法计算过程如下：

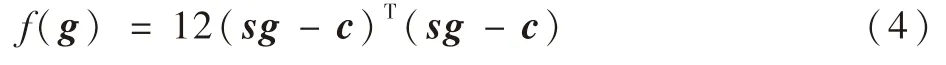
把式（3）展开为函数f（g）的最速下降方向，即梯度为

以LBP算法作为图像初值，Landweber算法为

设λmax为sTs的最大特征值，α≤2λmax保证Landweber算法收敛。

3.3 CG算法

CG算法计算过程为：在式（7）的两边乘以S的转置矩阵ST，得到式（8）。

式中：S为灵敏度矩阵；G为介电常数矩阵；C为电容值。

1）记初始灰度值为向量G0，设为零向量。

2）给定参数令STS＝S′，STC＝C′，得到新的未知方程S′G＝C′。r0＝C′－S′G0，p0＝r0；进行循环迭代计算。

3）当k＝0，1，2，…，n时，进行循环计算。

式中：pk为第k次的搜索方向；rk为残差向量。

转到式（11）。

3.4 BICG算法

BICG算法计算过程如下：

1）记初始灰度值为向量G0，设为零向量。

2）给定参数r0＝C′－S′G0，p0＝r0，pt0＝rt0，rt0为r0的共轭矩阵；进行循环迭代计算。

3）当k＝0，1，2，…，n时，进行循环计算。

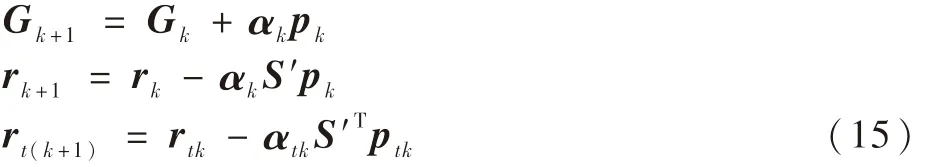
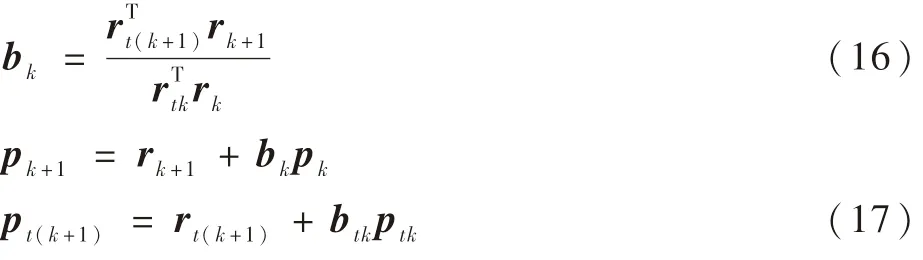
转到式（16）。

3.5 Tikhonov算法

正则化算法是以最小二乘准则及平滑准则作为理论依据计算的，目标泛函为

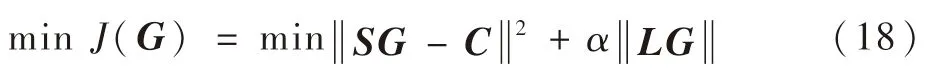
式中：α为正则化参数；L为正则化算子。

对于给定的正则化算子L，选取合适的正则化参数α＞0，最小化方程，可以得到Tikhonov算法的解为

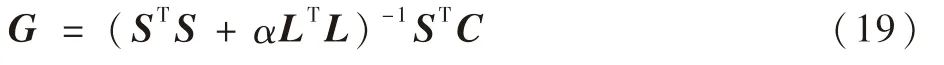
其原理就是引入一个正则化参数，使原来不能求逆的矩阵可以求逆矩阵。设L为单位矩阵，可得标准Tikhonov算法的解为

正则化参数α的取值是至关重要的，直接影响到图像重建的质量，而且正则化参数α的选择是很难确定的。本文实验选取的正则化参数为0.003。

3.6 改进算法

本文改进算法是在BICG算法基础上加入了正则化的思想。传统的BICG算法应用时针对不同的流型所要的迭代次数会有很大的变化，为了改进这一不足，加入了正则化的思想。将BICG算法经过Tikhonov正则化后变为

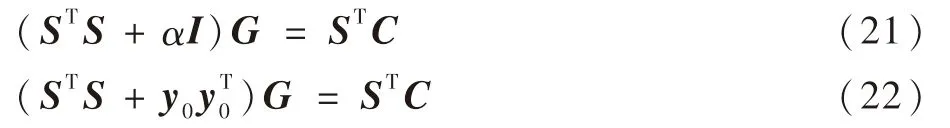
式中：y0＝STx0，x0为正则化向量。选取合适的x0，令y0＝STx0，S′＝STS＋y0yT0，取初始灰度值G0为零向量，r0＝C′－S′G0，p0＝r0，其循环迭代过程与BICG算法相同。

4 实验与分析

4.1 图像重建

运行MATLAB 2014a软件，首先，对建模完成的程序分别进行空场、物场、满场电容值和灵敏度的计算，并进行归一化处理；其次，分别通过Tikhonov算法、Landweber算法、CG算法、BICG算法及改进算法等5种算法对各模型进行图像重建。仿真模型选择核心流、双泡流、三泡流、层流和环流。图像重建结果如图5所示。

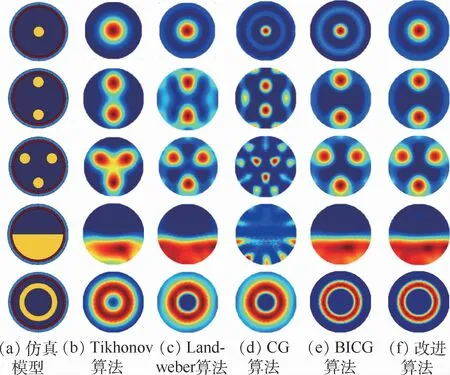
图5 各模型重建图像Fig.5 Reconstructed images of each model

4.2 图像重建分析

仿真实验中，通过计算重建图像的图像错误率（IME）和图像相关系数（CORR）来对重建图像进行评估，对重建图像的效果进行评价［14-15］。将Tikhonov算法、Landweber算法、CG算法、BICG算法及改进算法的重建图像的图像错误率和图像相关系数进行对比，分析改进算法的成像优缺点。图像错误率IME和图像相关系数CORR的计算公式分别为

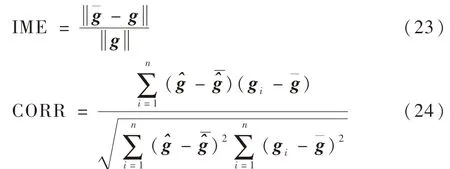
由式（23）和式（24）计算得IME和CORR，分别如表1和表2所示。

通过数据对比可以看出，使用CG算法得到核心流模型的成像效果最佳，改进算法效果也相差不大，但BICG算法迭代次数少，成像时间快，效率会更高一些。一般使用核心流模型验证传感器系统的基本性能。反观其他模型的图像重建数据对比，BICG算法和改进算法成像效果优于其他成像算法，尤其在环流模型中，其成像效果远远超出其他算法。

表1 IME计算值Tab le 1 Calcu lated values of IM E

实验中，除了计算图像错误率和相关系数，还对各算法成像时间和迭代算法的迭代次数做了统计。表3为各成像算法数据对比。通过多次调节对比，各迭代算法选取的迭代次数不同，选择各算法最优成像效果。通过选择的迭代次数进行成像时长对比。由数据可以直接看出，改进算法迭代次数相对其他迭代类算法大大减少，而且成像时间也大大缩短。

表2 CORR计算值Table 2 Calculated values of CORR

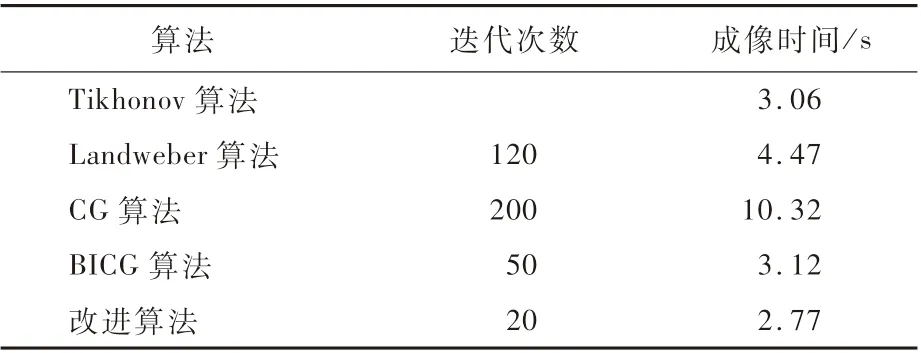
表3 成像算法数据对比Table 3 Com parison of im aging algorithm data

5 结 论

1）本文提出了将BICG算法应用到ECT技术，而且图像重建的分辨率更高，误差减小，通过仿真实验可以发现BICG算法的可行性，不同的流型都具有较好的成像效果，得到更高质量的重建图像，大幅度缩短重建图像的成像时间，可以更好地应用于在线监测。

2）针对不同流型所对应的参数和迭代次数有所不同，而且变化幅度较大，在实际应用中可能会受到一些约束，为此将BICG算法与正则化算法相结合，通过调节一个正则化参数便可得到较好的成像效果。

3）为使改进算法在ECT技术和其他领域可以得到更广泛、更有效的应用，还需要对其进行进一步的研究和发展。