微型探头-传感系统高频响应特性模型适应性

丁红兵，李一鸣，李金霞，王超

（天津大学 电气自动化与信息工程学院，天津300072）

瞬态压力测量，在航空航天、国防、工业等领域起着重要作用［1-3］。在航空发动机型号研制过程中，瞬态压力测量用来测试压气机转子后流场，描述非定常流动特征［4-5］；气固流化床内水动力现象的研究，以及流化床行为的表征都需要局部瞬态压力波动的测量［6-7］；在燃气轮机的测控系统中，瞬态压力的测量可用来检测发动机内部的流量异常［8］。为了保证测量的可靠性，应尽量减小对流场的扰动，因此，微型探头-传感系统在瞬态压力测量中起着非常重要的作用。微型探头-传感系统除了压力传感器，还包括引压管和腔室，而引压管和腔室的频响特性通常都比较低，导致系统的可用频带变窄。当用于获取高频流场的动态特征时，其频响往往达不到测量要求，造成测量误差变大甚至信号失真。因此，有必要研究微型探头-传感系统的动态响应模型，以分析并改善其频响特性。

目前，很多文献都对微型探头-传感系统频响特性进行了理论研究并提出了不同的数学模型。柳兆荣等［9］根据流体阻抗法得到了固有频率公式，把探头-传感系统分成5种典型结构。探头-变送系统的数学模型主要分为集中参数模型和分布参数模型。叶挺 等［10］、黄俊钦［11］把探 头-传感系统看作是集中参数的不可压缩二阶系统，前者给出了探头-传感系统的幅频特性和固有频率表达式，结构比较简单，而后者给出了差分方程模型、离散传递函数模型和连续传递函数模型，与实验数据基本吻合。Goodson和Leonard［12］建立了系统的分布参数模型，并基于此给出了线性摩擦模型和耗散模型。在此基础上，Iberall［13］利用分布参数模型推导出了探头-传感系统的动态响应公式，但省略了推导过程，而且没有进行实验验证。Bergh和Tijdeman［14］以及Richards［15］沿用了Iberall的方法，给出了探头-传感系统的数学模型，并用实验验证了模型的准确性。这些模型为微型探头-传感系统频率特性的研究提供了依据，但是大部分模型并没有给出具体的适用范围和预测精度，对瞬态压力信号，尤其是高频信号的测量精度难以保证，可能影响瞬态压力信号的分析结果。因此，针对微型探头-传感系统的具体结构，如何选择合适的数学模型，是一个亟待解决的问题。

本文对微型探头-传感系统进行分类，并利用基于CFD数值模拟的系统参数辨识方法得到频响函数，以谐振频率、截止频率和工作频带为性能指标，对微型探头-传感系统的经典数学模型进行定量评价。

1 微型探头-传感系统频响特性

微型探头-传感系统由压力传感器、引压管和腔室构成，其结构图如图1所示，r表示引压管半径，l表示引压管长度，V表示腔室体积。

瞬态压力信号作为微型探头-传感系统的输入信号pi，可以表示为不同频率正弦信号的合成，所测信号为输出信号po，频响特性反映正弦信号作用下系统响应的性能［16］。稳定系统的频响特性等于输出和输入的傅里叶变换之比，即式中：ω为角频率；A（ω）为幅频特性；φ（ω）为相频特性，分别为输出响应中与输入同频率的谐波分量与谐波输入的幅值比和相位差。

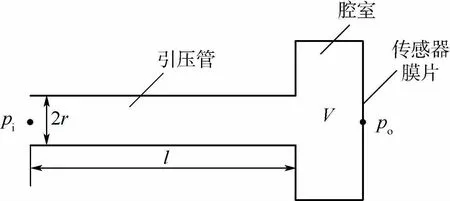
图1 微型探头-传感系统基本结构Fig.1 Basic structure ofmicro probe-transducer system

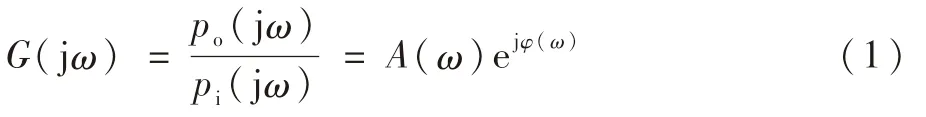
2 微型探头-传感系统结构分类及判定

根据引压管和腔室尺寸的不同，对基于流体阻抗法得到的微型探头-传感系统固有频率公式进行合理的简化，从而得到5种典型结构［9］，如表1所示。其中：a为管道截面积，c为声速，ωn为固有频率，R为腔室半径，L为腔室长度。由于流体阻抗法忽略了流体黏性，系统阻尼非常小，此时ωn近似等于谐振频率ωr。结构Ⅳ的腔室长度不断减小，当远小于引压管长度时，可将腔室作为集中参数处理，这时可看作结构Ⅲ。结构Ⅰ和结构Ⅱ则分别是结构Ⅲ引压管长度非常小和腔室体积非常小时的简化结构。

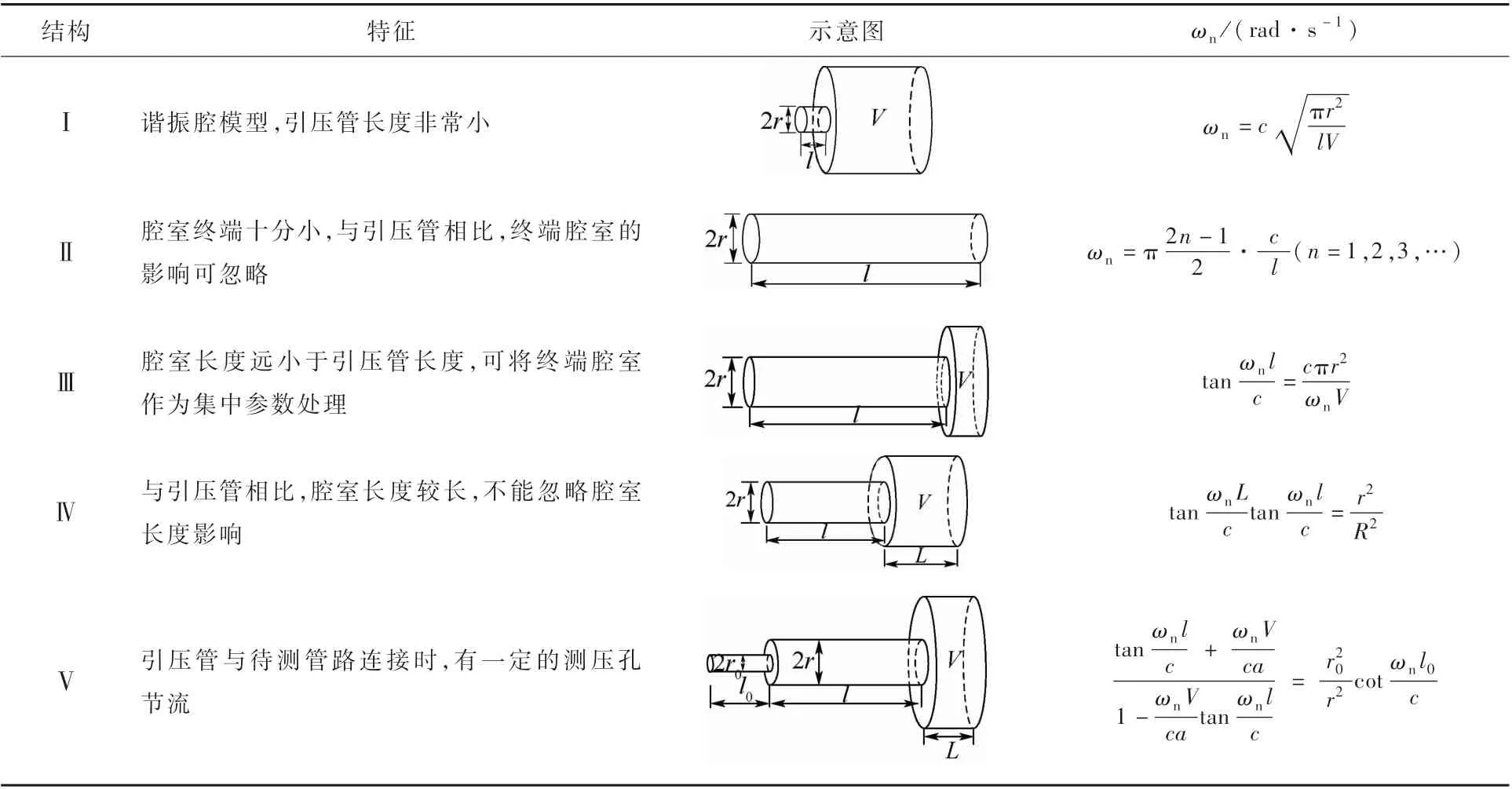
表1 微型探头-传感系统典型结构Tab le 1 Typ ical structures of m icro p robe-transducer system

3 微型探头-传感系统数学模型

假设微型探头-传感系统引压管半径r远小于长度l，传感器的频响特性是理想的，且管道及腔室外壁是刚性的，表2所示为已有研究中所提到的6种数学模型。其中：c0为平均声速；Jn（n＝0，1，2）表示n阶第一类贝塞尔函数；m表示第m个微型探头-传感系统；n为多变常数类型；Pr为普朗特数；μ为流体动力黏度；ρ为流体密度；σ为由于膜片偏转引起的腔室体积增加；γ为比热比。当Rf／ω≪1时，Rf＝8μ／（ρr2），表2中的线性摩擦模型和耗散模型可以简化为附录A中式（A1），以减少实际计算中的困难。

上述数学模型仍存在不完善的地方需要进一步修正。由于上述模型均忽略了腔室内的流速，因此理论上不适用于结构Ⅰ谐振腔的预测［18］，结构Ⅰ计算将在第5节详细说明。另外，对于微型探头-传感系统，其腔室体积V很小，这时管道内流体的可压缩性和传感器柔性造成的腔室体积变化就不能完全忽略不计，造成不可压缩二阶系统模型不适用，因此用等效腔室体积Ve＝V＋Vf＋Vte代替公式中的V［19］。Vf为考虑传感器柔性的附加容积，Vf＝E（ΔVf／Δp），ΔVf／Δp表示传感器在单位压力作用下的体积变化，E为流体体积模量；Vte为考虑流体管道可压缩性的附加容积，Vte＝（4／π2）／（al）。

对于结构Ⅱ，腔室体积为0，此时，可压缩流体管道模型（无损耗模型、线性摩擦模型和耗散模型）的频响特性公式可简化为

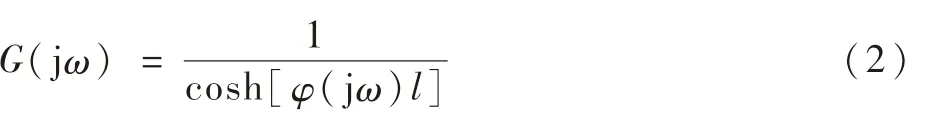
整理可得到系统的谐振频率公式为

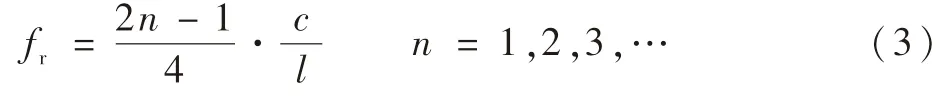
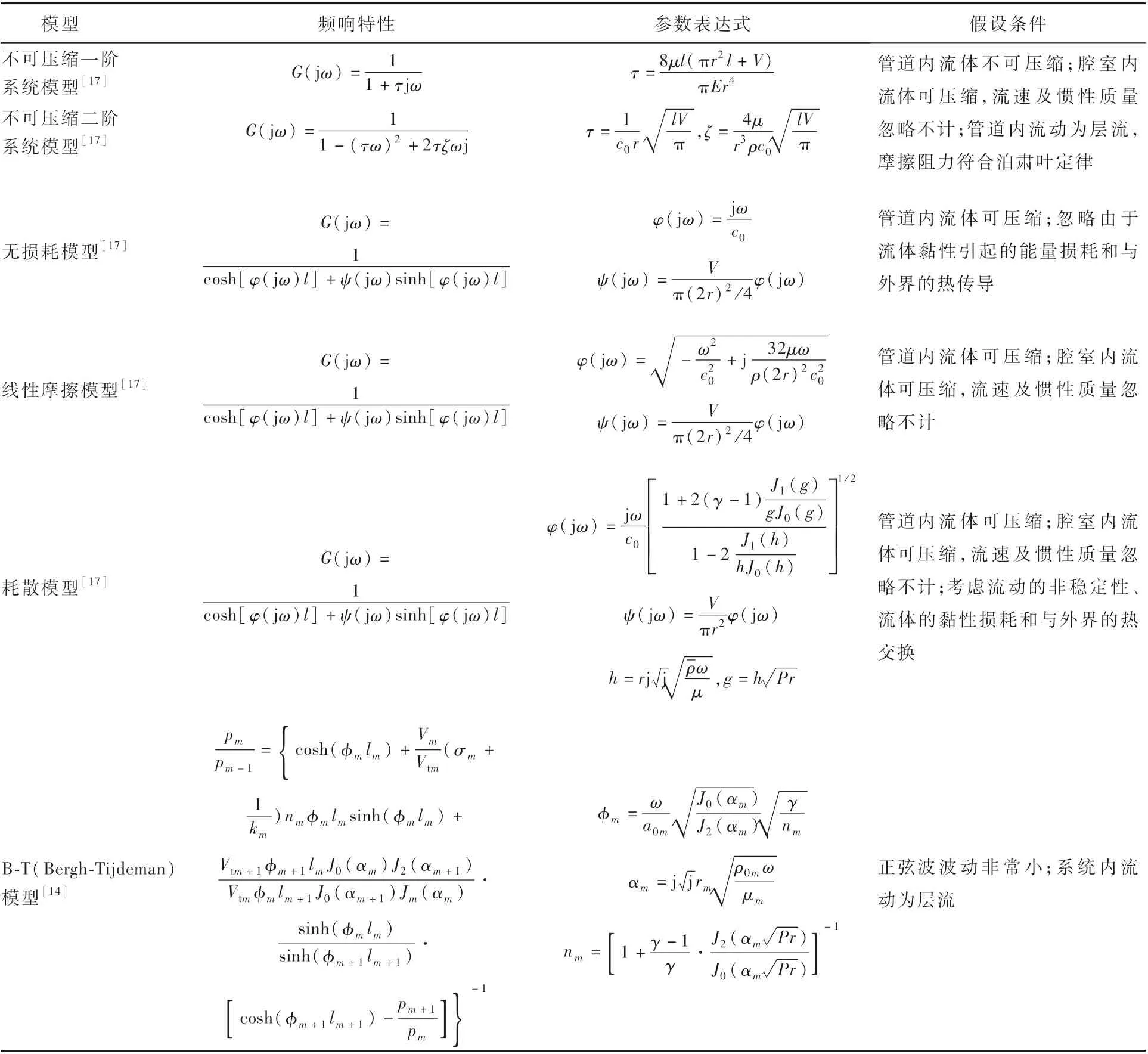
表2 微型探头-传感系统数学模型Tab le 2 M athem aticalm odels of m icro p robe-transducer system

仅考虑第一个谐振频率，即n＝1时，就是著名的四分之一波长公式。

对于B-T模型，当m＝N＝2时，表示系统由2个引压管和2个腔室构成，令第1个腔室的体积为0，即V1＝0，即可用于结构Ⅴ的计算。

微型探头-传感系统内的流场十分复杂，在不同的假设条件下，每种模型适用于特定的工况条件和系统结构，但目前这些模型的适用性与系统结构之间没有明确的对应关系，缺少对于模型误差的评估。因此，利用CFD数值模拟的方法对微型探头-传感系统进行系统辨识，并对上述数学模型进行适用性分析和预测精度评价。

4 CFD数值模拟及验证

利用ANSYS® FLUENT进行CFD数值模拟。采用结构化网格划分，湍流模型选用标准k-ε模型。考虑可压缩性，流体设置为理想气体，并打开能量方程。系统内部由流体速度和密度的变化引起压力振荡。入口采用压力入口边界条件，由于出口为传感器膜片，因此出口和壁面都设为无滑移壁面。监测点为入口和出口壁面中心处，监测流场压力变化。采用双精度求解器以提高仿真精度。为真实反映系统内部的流场，采用三维网格，如图2所示。

为了检验数值模型和数值方法的可靠性，将仿真结果与Bergh和Tijdeman［14］的实验进行对比。实验的环境压力为105 020 Pa，温度为24℃。微型探头-传感系统入口为正弦压力扰动，幅值为650 Pa，在10～200 Hz的频率范围内测量系统的动态响应，引压管半径r＝0.525mm，引压管长度l＝500mm，腔室体积V＝285mm3。

通过CFD数值仿真，分别利用正弦激励法和阶跃激励法得到系统的频响特性。

正弦激励法的入口施加固定幅值、不同频率的正弦压力信号，每周期采样点数N＝100，输出同样为正弦信号。通过傅里叶变换将时域信号转换到频域，并利用比值校正法对频域信号进行校正，得到信号的幅值和初始相角，最终可得到输出与输入信号的幅值比A（ω）和相位差φ（ω），根据式（1），即可得到频响特性G（jω）。数值仿真结果如图3（a）所示。

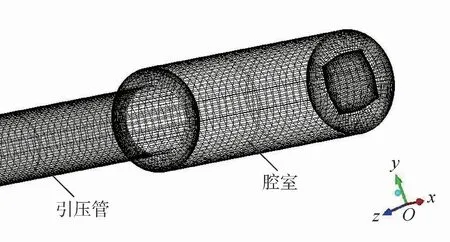
图2 微型探头-传感系统网格Fig.2 Grid ofmicro probe-transducer system

对于阶跃激励法，对入口施加固定幅值（pi＝100 Pa）的阶跃压力信号，监测出口的压力响应，通过系统辨识得到系统传递函数，从而得到其频率特性G（jω）。数值仿真结果如图3（b）所示。利用非线性最小二乘法，对系统频率响应函数进行参数辨识。由于压力波从入口到传感器膜片的传播需要一定时间，因此模型需考虑延迟时间τd，其计算公式为

τd＝（l＋L）／c （4）

模型的阶次利用各个拟合阶次的残差平方和构成的损失函数Qn来确定［20］。Qn表示n阶预测模型的残差平方和。系统各阶次Qn的变化趋势如图4所示。Q2与Q1相比，有比较大的下降，Q3的下降趋势明显变缓，而从Q4开始，变化十分微弱。根据最终陡峭下降准则，判断系统阶次最低为二阶。

为了设置合适的采样频率fs，根据式（5）选取［21］：

图3 正弦激励法和阶跃激励法CFD数值仿真结果Fig.3 CFD simulation results of sine and step excitation methods

式中：T95为阶跃响应调节时间的95%。

以fs＝5 000 Hz为例，其辨识得到的系统频响函数为式中：τd＝0.001 5；a1＝0.12；a2＝411.44；a3＝3.40×105；b1＝438.38；b2＝3.40×105。

为确定合适的采样频率，还分别取fs＝2 000 Hz和fs＝4 000 Hz进行了CFD仿真和参数辨识，并与正弦激励结果和实验得到的幅值比及相位差进行对比，结果如图5所示。可知，当采样频率为fs＝5000Hz时，阶跃激励法与正弦激励法和实验结果吻合良好，说明基于CFD的系统辨识方法，可用于微型探头-传感系统频响特性的定量研究。关于采样频率的选择，如果fs太小，会因仿真精度不够造成预测误差；若采样频率fs过大，则可能会因为畸变问题而造成误差，所以需要选择合适的采样频率。本文设置采样频率fs为所关心频段最高频率的25倍，以保证预测精度。

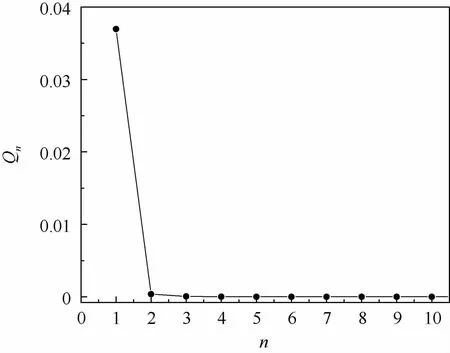
图4 Qn随n的变化趋势Fig.4 Variation of Qn with n

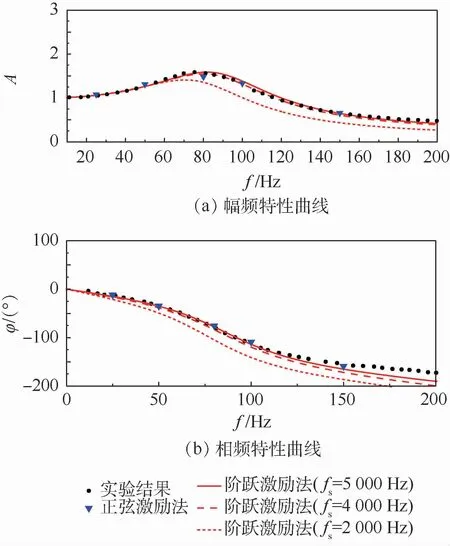
图5 实验和CFD数值仿真得到的频响特性曲线Fig.5 Frequency response characteristic curves obtained by experiment and CFD simulation

5 不同结构下数学模型适应性分析

传感器常用的频响特性指标是谐振频率ωr、闭环截止频率ωb和工作频带ωg。为保证能够测得较高能量的信号，本文规定ωb为系统闭环幅频特性下降到0 dB时对应的频率，即A（ωb）＝1。工作频带ωg是动态幅值误差为±5%所确定的有效工作频率范围，如图6所示。

不可压缩一阶系统模型是二阶系统模型的一种特殊情况，仅适用于压力变化缓慢的情况，是二阶系统模型的近似，不能预测欠阻尼二阶系统的谐振频率。无损耗模型是线性摩擦模型的特例，在其推导过程中，认为流体与管道的摩擦力为0，因此公式变得简单，精度较低。在下面的研究工作中，不可压缩一阶系统模型和无损耗模型本文将不做进一步分析。

利用4种模型对结构Ⅱ～结构Ⅴ的微型探头-传感系统进行分析，尺寸如表3所示。截止频率和工作频带可以衡量微型探头-传感系统的可用带宽以及准确度，因此以这2个参数为指标对各数学模型做定量评价。

图6 微型探头-传感系统的幅频特性曲线Fig.6 Amp litude-frequency characteristic curve of micro probe-transducer system

表3 微型探头-传感系统尺寸Table 3 Size ofm icro probe-transducer system s

理论截止频率fb0、工作频带fg0及不可压缩二阶系统模型、线性摩擦模型、耗散模型和B-T模型计算得到截止频率fb1～fb4、工作频带fg1～fg4如表4和表5所示，σf表示相对误差。其中实验结果参考自文献［14，22］。由表4和表5可知，实验仅针对于频率特性较低的系统，而且并不能覆盖所有系统结构，而数值模拟可作为对实验的补充和完善。综合2种方法的结果来看，B-T模型的精度最高，且适用于较复杂的结构Ⅴ。

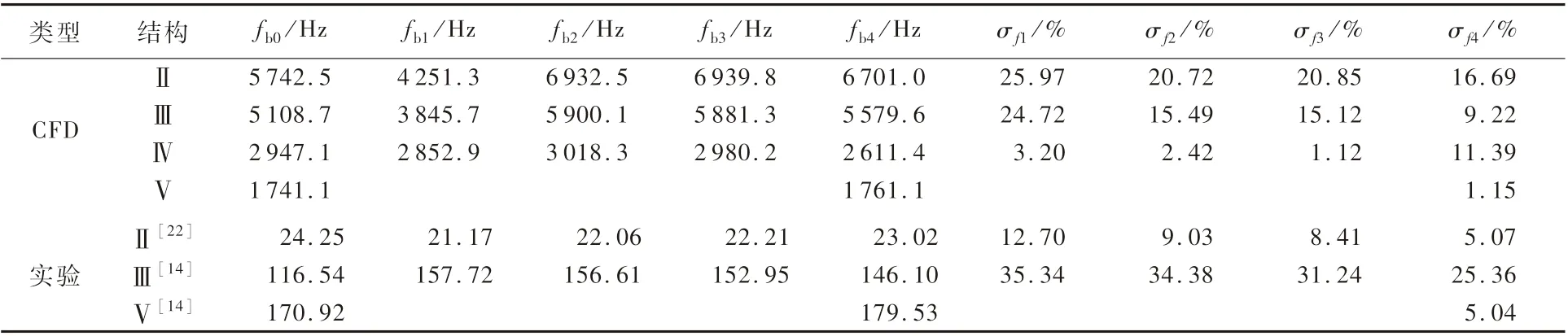
表4 4种预测模型的截止频率计算结果及误差Tab le 4 Cut-off frequency com putational resu lt and er ror of four p rediction m odels

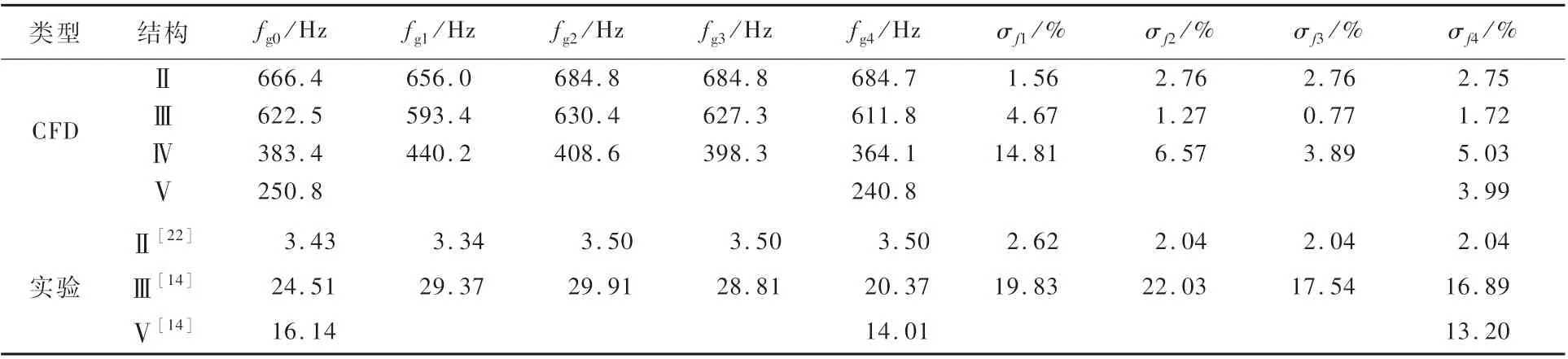
表5 4种预测模型的工作频带计算结果及误差Tab le 5 W orking frequency band com putational resu lt and error of four p red iction m odels

对于引压管较短的结构Ⅰ，以上4种模型会产生较大的计算误差，以B-T模型为例，如图7所示，从l／d＝1开始，随着l不断减小，B-T模型的误差越来越大［23］。其中：d为引压管直径。

Panton和Miller［24］针对这种情况，提出了结构Ⅰ谐振频率的计算公式：

式中：l′＝l＋Δl为有效长度，Δl＝8r／（3π）·（1－1.24 r／R）为对引压管长的修正；S为引压管横截面积；kL＝ωrL／c。对式（7）右边展开得到

如果仅保留式（7）右边第一项，整理可得到谐振频率的经典计算公式：

如果保留前两项，则得到谐振频率的改进计算公式：

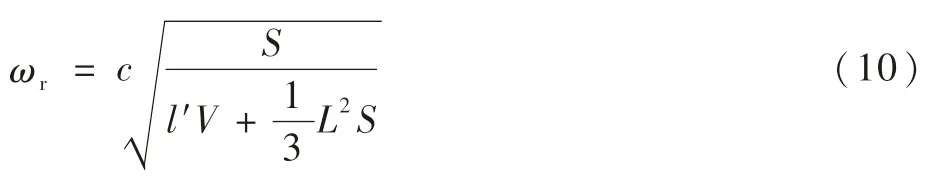
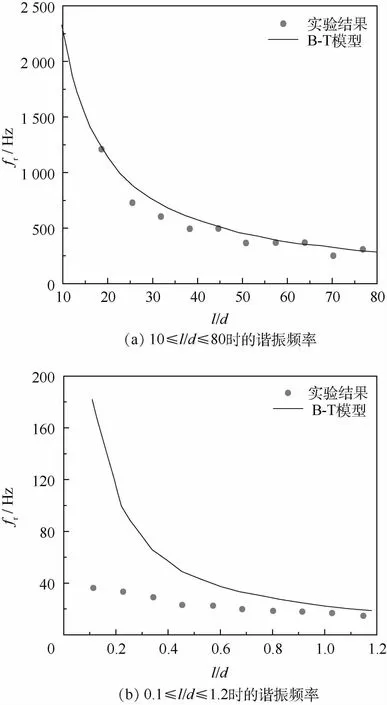
图7 不同l／d条件下的谐振频率Fig.7 Resonant frequency under different l／d

Panton和Miller［24］通过实验得到了不同l／d条件下系统的谐振频率fexp，结果如表6所示，f1、f2和f3分别为式（7）、式（9）和式（10）的预测结果。由表6可知，式（7）（原始公式）的预测误差小于1%，式（10）（改进公式）小于3%，对结构Ⅰ有很高的预测精度。对于式（9）（经典公式），当l／d＝0.63，即引压管较长时，其误差在6%左右；当l／d＜0.42，即引压管较短时，其误差明显增大。

综合以上分析，总结微型探头-传感系统不同结构对各模型的适应性如表7所示。

表6 Panton模型谐振频率实验与预测结果对比［24］Table 6 Com parison ofm easured and predicted resonant frequencies w ith Panton m odel［24］

表7 微型探头-传感系统不同结构对各模型的适应性Table 7 Adaptability of differentm icro probetransducer system structu res to various m odels

6 瞬态压力测量的应用

声速喷嘴中流动的蒸汽或含湿气体由于自身温降会发生凝结，造成非稳态自激振荡现象，影响喷嘴的计量精度。为了获得自激振荡的高频瞬态压力信号［25］，在喷嘴壁面设置引压孔，以安装微型探头-传感系统。实验所用喷嘴尺寸如图8所示，且喷嘴壁面厚度为6.5 mm。根据半经验公式［26］，预估自激振荡频率在9 368～15 806 Hz范围内。因此，要求微型探头-传感系统的截止频率大于15806Hz。

为了减少对喷嘴内流场的扰动，设计微型探头-传感系统为带有节流孔的结构Ⅴ。选择B-T模型设计系统尺寸。根据B-T模型可知，微型探头-传感系统的截止频率随测压孔半径r0的增大而增大，而测压孔长度l0、引压管半径r、引压管长度l和腔室体积V的增大则会降低截止频率。

对于小喉径喷嘴来说，测压孔对流场的影响是很显著的，因此r0必须很小，要求测压孔半径满足0mm＜r0＜1mm，引压管半径则应满足r＞r0。为了便于安装，测压孔长度l0与引压管长度l之和取喷嘴壁厚，即l0＋l＝6.5mm。而为了补偿测压孔半径减小所造成的截止频率的降低，则应尽量减小l0、r、l和V以提高截止频率。

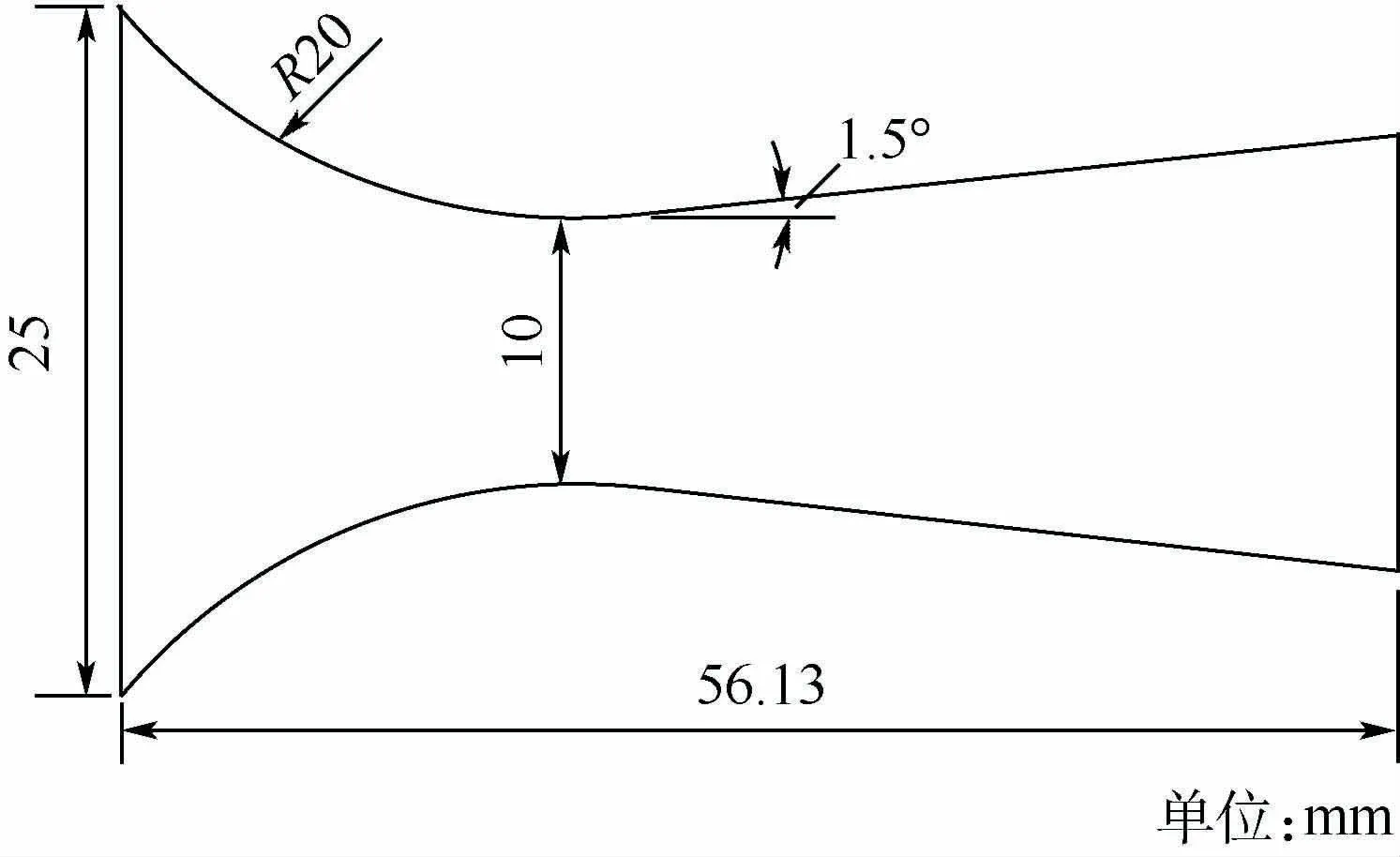
图8 声速喷嘴尺寸Fig.8 Size of sonic nozzle

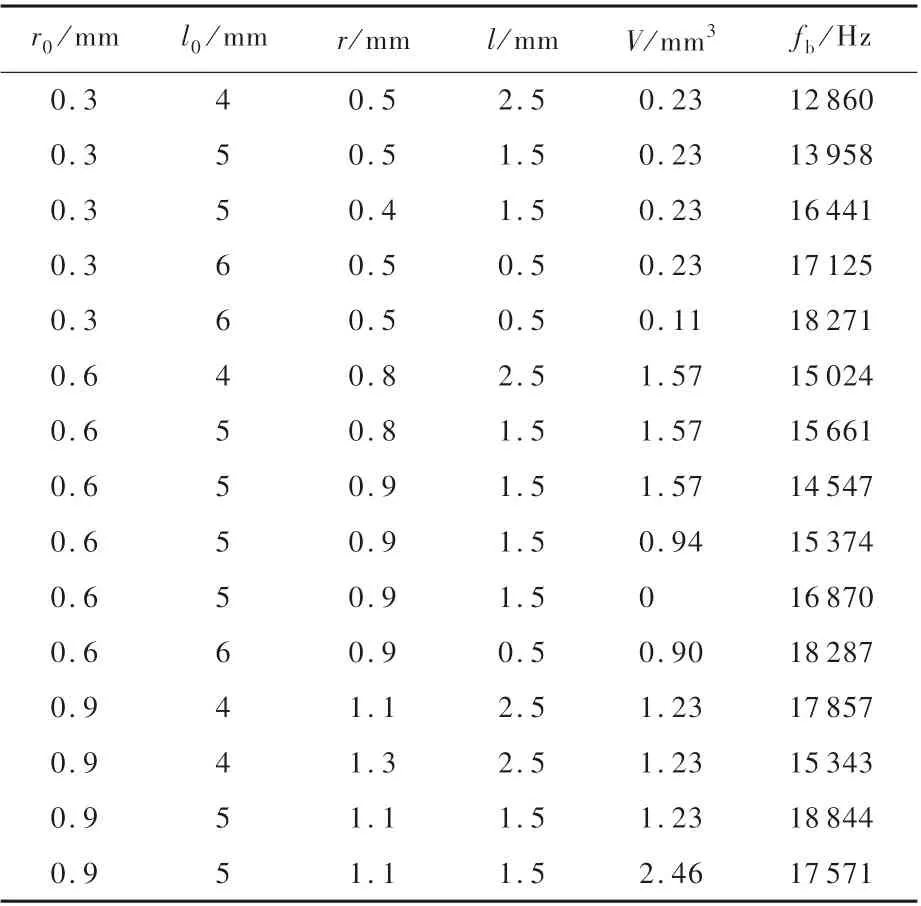
表8 微型探头-传感系统尺寸及闭环截止频率Tab le 8 Size and closed-loop cut-off frequency of m icro p robe-transducer system

基于以上尺寸范围，取若干种微型探头-传感系统，利用B-T模型计算得到相应的闭环截止频率fb，如表8所示。首先选取fb＞15 806 Hz所对应的尺寸，而为了减少对流场的扰动，进一步选择较 小的测压孔半径r0＝0.3 mm或r0＝0.6 mm。但由于喷嘴壁面打孔和传感器加工的限制，测压孔做不到太小。另外，腔室部分也不能太小，需要为传感器敏感元件的安装和接线预留一定的空间。最终选择r0＝0.6mm，l0＝5mm，r＝0.9mm，l＝1.5mm，V＝0mm3，此时敏感元件直接安装在引压管顶端，微型探头-传感系统的闭环截止频率fb＝16 870Hz。

利用微型探头-传感系统测量自激振荡瞬态压力信号，通过傅里叶变换将时域信号转换到频域，并利用比值校正法对频域信号进行校正，结果如图9所示，幅值最大处对应的即为自激振荡频率13 950 Hz。表明所设计的微型探头-传感系统可以有效测得超声速凝结中的高频瞬态压力信号。

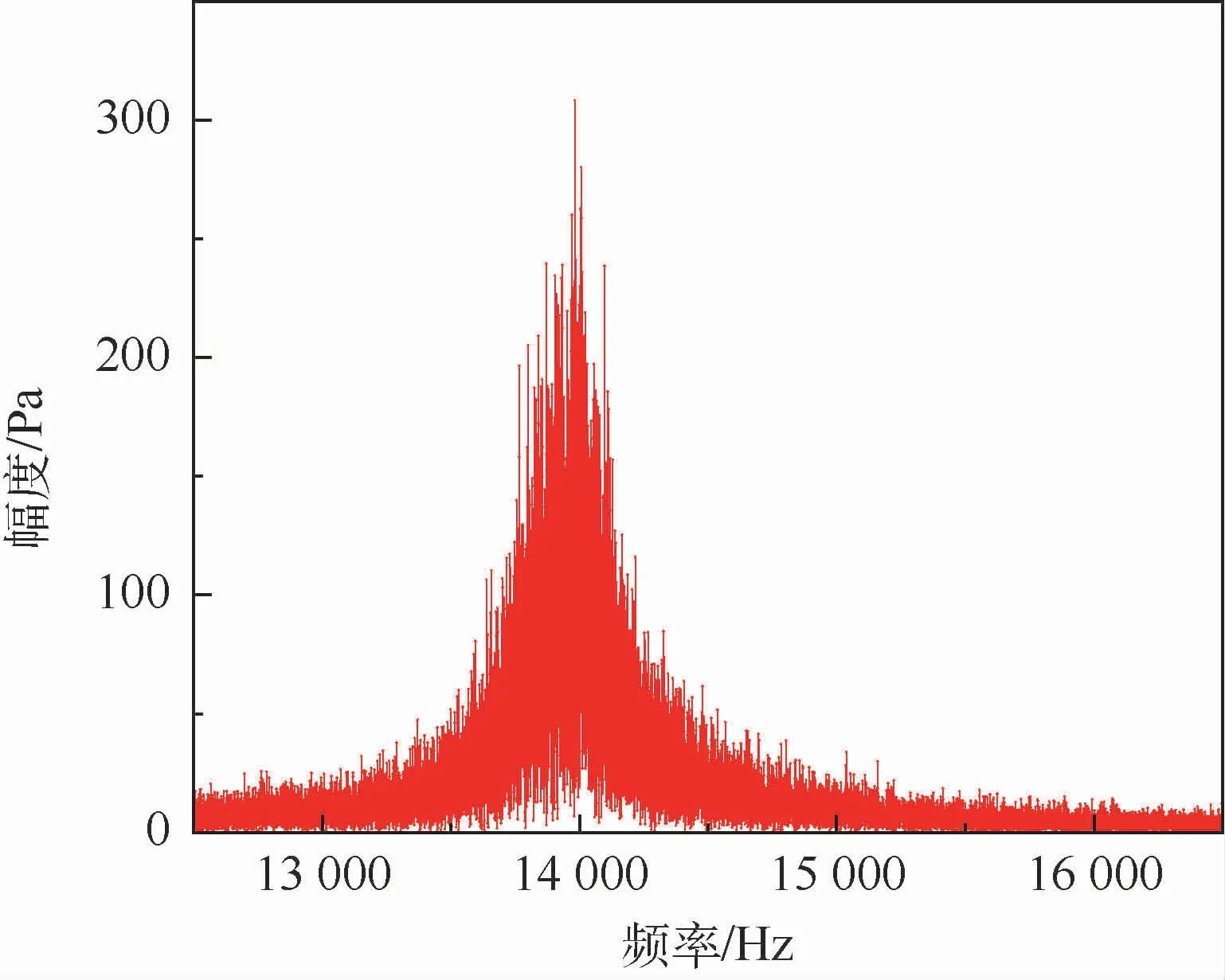
图9 凝结自激振荡频域信号Fig.9 Signal of self-excited oscillation in frequency domain

7 结 论

本文首先基于流体阻抗法得到的固有频率公式，对5种典型结构的微型探头-传感系统进行了判定和划分，综述了现有微型探头-传感系统的频响预测模型、假设条件及模型修正方法。为对理论数学模型进行定量评价，提出了基于CFD的系统辨识方法并进行了实验验证。根据辨识的频响函数，计算得到了不同结构微型探头-传感系统的谐振频率、截止频率和工作频带（幅值误差±5%），并与数值模拟和实验得到的理论预测结果进行了对比。可得到以下结论：

1）对结构Ⅰ的引压管长进行修正后，Panton模型可用于计算其谐振频率。工程实际中，可利用模型简化后的经典公式或改进公式，但当l／d＜0.42，即管长较短时，经典公式的误差较大。如果需要精确计算，则使用模型的原始公式。

2）对于结构Ⅱ，在工程中，可利用四分之一波长理论公式计算其谐振频率；如果精确计算其频率特性，可选择B-T模型。

3）当粗略估算结构Ⅲ的最低阶共振频率时，可选择不可压缩二阶系统模型；而精确计算时，可选择线性摩擦模型、耗散模型和B-T模型。其中，线性摩擦模型计算简单且适用于低频扰动情况，B-T模型精度最高。

4）结构Ⅳ和结构Ⅴ利用B-T模型计算精度较高，其中结构Ⅳ可看作结构Ⅴ腔室体积为0的一种特殊情况。

利用上述研究结果对实验用微型探头-传感系统进行了优化设计，并用于超声速凝结自激振荡现象的研究。结果表明，优化的微型探头-传感系统频响特性可满足高频（约10 kHz）压力波动信号的动态测量需求。

本文为计算微型探头-传感系统频率特性提供了依据，便于工程应用中根据实际情况选择合适的预测模型，从而进一步改善微型探头-传感系统的性能，提高瞬态压力测量的准确性。