空间光学遥感器真空热试验工装模块化设计

周泽鑫，孙志强，*，徐冰，2，洪扬，2

（1.中南大学 能源科学与工程学院，长沙410083； 2.北京空间机电研究所，北京100076）

空间光学遥感器是搭载在卫星或航天飞行器上利用光学技术获取目标属性和相关信息的精密科学设备。为了适应光学遥感技术的快速发展，对光学遥感器的要求逐渐向高空间分辨率、高光谱分辨率、高辐射分辨率性能及轻量化的方向发展。而光学遥感器作为卫星有效载荷，对环境温度均匀性的要求将变得更加苛刻，均匀的温度场可为其提供良好的工作环境［1-2］。目前，为保证遥感器在轨正常工作，顺利成像，会对其增添热控装置来保证温度分布的均匀度满足所需要求。而检验其温度分布情况的有效途径之一，就是在环境效应充分研究的基础上，对光学遥感器进行充分而又适度的空间环境地面模拟试验（简称环模试验）。通过环模试验发现隐患、改进设计、避免早期失效，从而提高光学遥感器工作的可靠性［3］。

在环模试验中，热沉装置在外，模拟了光学遥感器在太空工作时真空、冷、黑的背景环境，热沉内部放置包含了热控设备的光学遥感器，来模拟在轨工作状态。热控的精度决定了试验的可靠性，目前在航天领域，光学遥感器热控制方式以被动热控为主，主动控制为辅，并采用成熟的热控制技术和实施工艺［4-6］，通常由预埋或者外贴高导热材料或热管等来提供光学遥感器所需的温度环境［7-9］。欧洲多个微型卫星通过安装U型热管来实现卫星温度场的均匀化［10］。胡帼杰等［11］通过优化散热面组合方式并运用三维热管网络的方法来实现所需热控要求，但难以应用在小型、热控要求高的卫星上。

模块化设计指在一定范围内将不同功能、不同规格、不同样式的模块组合在一起，来满足不同的设计需求。其中各模块具有独立的功能和结构，可以根据设计需求进行自由组合，具有良好的重构性，可以缩短产品的制作周期。而在环模试验中，对光学遥感器工装的设计和制造占其很大比重，其设计、制造周期影响整个遥感器的试验周期，目前工装从设计到成型需要数月的时间，周期太长影响试验进度，并且一型号一专用工装，造成了资源浪费。而对遥感器工装进行模块化设计可以简化设计流程、减少开发成本、缩短研制周期，实现工装的快速设计、快速装配、快速成型［12-17］。

本文以某型号空间光学遥感器为研究对象，试验时将舱板以工装的方式固定在遥感器的6面，在舱板表面外贴加热片，通过改变加热片发热量来满足遥感器热控要求。目前由于舱板外部环境复杂，导致舱板受热不均，无法保证遥感器温度均匀性的要求。针对上述问题，本文提出对舱板进行模块化设计的方法，将一整块舱板分割成数个小模块，对每个小模块分别贴加热片来进行热控，从而提高舱板温度均匀性，进而保证遥感器正常工作。

1 物理模型

本文的环模试验系统如图1所示。光学遥感器及其电子学设备舱安装在热沉装置中，光学遥感器的各舱板构成一个近似封闭的六面体，分别对应±X、±Y、±Z六块舱板，各舱板之间的位置关系如图2所示。－X舱板有3条安装块，连接相机与钢架起固定作用；＋Y舱板开有2个方孔与散热板相连；＋Z舱板开有2个圆孔，用于相机对外部环境进行拍摄；－Z舱板开有2个方孔，用于相机与电子学设备舱的连接。各舱板的温度分布要求为：舱板各处实际温度不得高出热控要求2 K，不得低于热控要求，在高精度工作状态时，实际温度不得高出热控温度1 K。本文为方便表达，将舱板实际温度与热控要求的差值称为温度偏差，实际温度高于热控要求则称为正偏差，反之为负偏差。表1给出了该型号光学遥感器在某一工作状态下各舱板的热控要求。

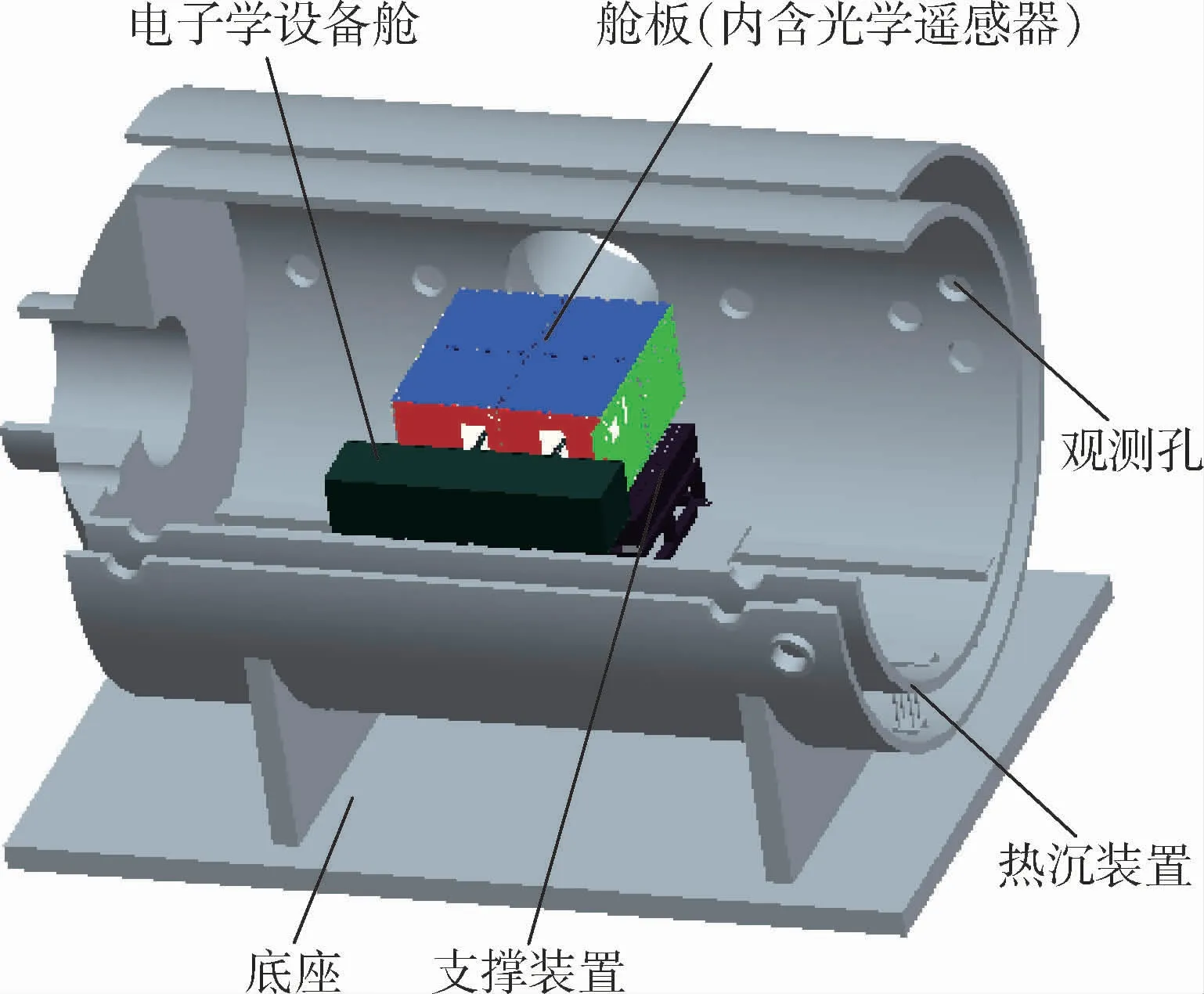
图1 空间环模地面模拟试验系统Fig.1 System of space environment ground simulation experiment

本文在环模试验中，加热片与舱板之间粘贴热电偶来监测各舱板的温度分布情况。为保证监测的有效性，将热电偶均匀布置在每个舱板上，±X舱板热电偶为4×4分布；±Y、±Z舱板热电偶为3×4分布。受到舱板几何条件约束，需要对部分热电偶测点位置进行偏移或对测点个数进行删减。同时部分舱板区域受到多个辐射源综合影响，因此需要在该区域增加热电偶数量，来确保测量数据的有效性。在综合考虑舱板几何结构和舱板辐射环境后，最终热电偶个数为：＋X舱板16个、－X舱板27个、＋Y舱板14个、－Y舱板11个、±Z舱板各12个，共计92个。用热电偶实际测量温度与热控要求温度之间的温度偏差来表征舱板的温度均匀性，通过对92个测点进行计算分析发现，温度偏差最大可达4 K，多个测点出现了负偏差，温度偏差在0～2K之间所占比例为34.8%，温度偏差在0～1 K 之间所占比例为28.3%，表明工装的舱板温度均匀性差，试验结果不满足热控要求。

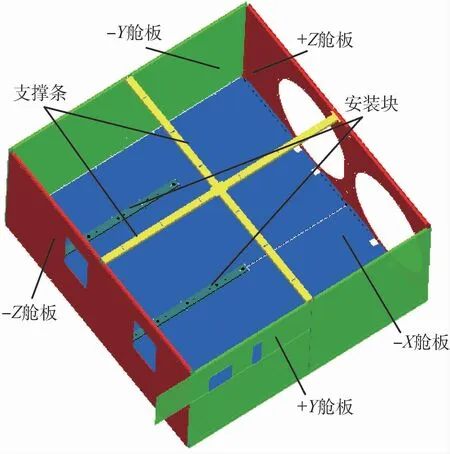
图2 工装模型Fig.2 Frock model

表1 舱板参数Tab le 1 Param eters of cabin p lates

2 数值计算模型

根据试验工装建立如图3所示的计算模型，并作如下简化和假设：由于各舱板均独立安装且未相连，因此忽略各舱板之间的导热，不考虑＋Y舱板超出－Z舱板外伸部分的影响，忽略底部3条安装块与钢架的漏热，所有舱板表面均为漫反射。舱板的具体参数列于表1中。底部钢架为恒定－60℃的结构钢，表面发射率为0.90；电子学设备舱表面温度恒定为20℃，与舱板正对面发射率为0.03，其余面发射率为0.90；散热板与光学遥感器相连，散去遥感器多余热量，保证其能够正常工作［18］，散热板表面温度恒为40℃，表面发射率为0.03。整个模型置于100 K 的真空环境中。

本文模拟所用软件为ANSYS，基于有限体积的数值模拟方法对舱板温度进行计算求解。电子学设备舱、散热板、底部钢架均设为定温壁面，各舱板表面设为耦合面，各表面初始温度均为293 K。计算中，能量方程采用二阶迎风差分格式。FLUENT中常用辐射模型有5种，其中DO（Discrete Ordinates）模型和S2S（Surface-To-Surface）模型精度较高［19］，而S2S模型更适用于计算没有参与性介质的封闭空间内的辐射换热［20］。因此，本文采用S2S辐射模型进行计算，此时能量守恒方程简化为

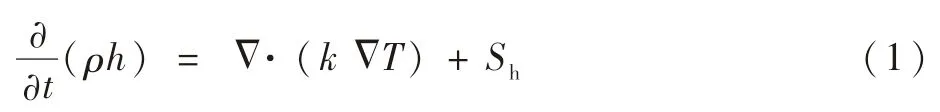
式中：t为时间；ρ为物体的密度；h为物体所含的总能；k为物体的导热系数；T为温度；Sh为仅包含辐射换热的源项。

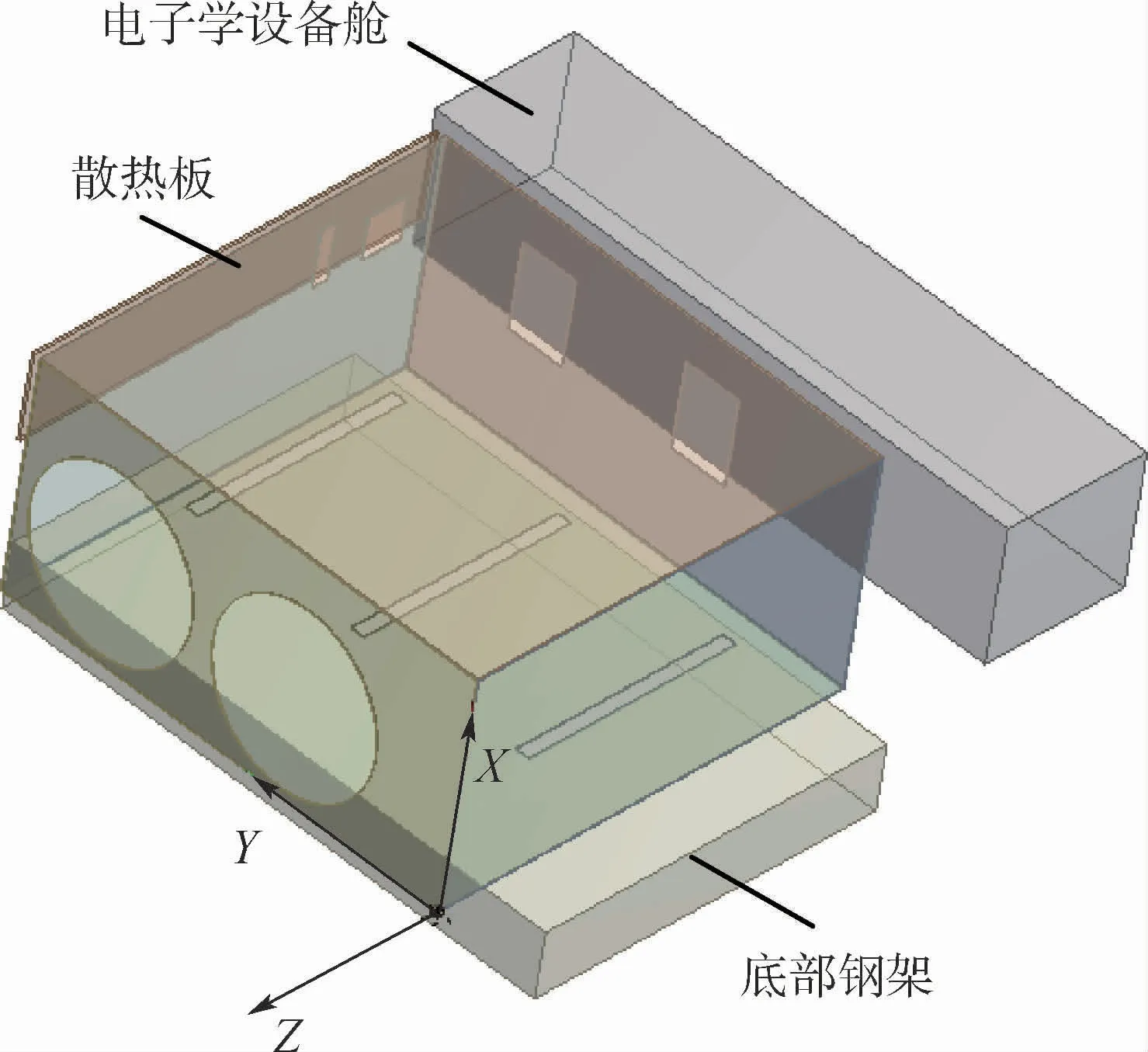
图3 计算模型Fig.3 Calculation model

合围空间内辐射换热计算式为

式中：Jk和Ek分别为从表面k发出的辐射和自身辐射；εk为表面k的辐射发射率；Fkj为k、j表面间的辐射角系数［21］，计算式为

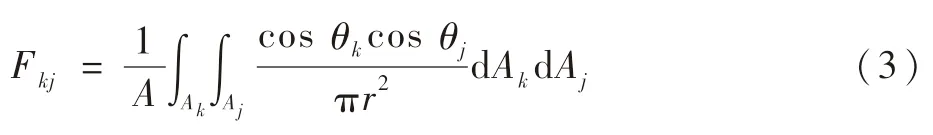
其中：A为微元表面的面积；r为微元表面之间的距离；θj、θk分别为微元表面d Aj、d Ak之间的连线方向与其法线方向的夹角［22］。

空间辐射区域以四面体网格为主，舱板为结构六面体网格，并在舱板厚度方向进行适度加密。首先进行网格无关性分析，采用3种不同疏密的网格进行模拟计算，网格数量分别取54万、138万、667万，根据各舱板的所需工况温度计算各舱板所需的热流密度，比较6个舱板热流密度的平均相对偏差，计算结果如表2所示。以网格数量为667万的计算结果为标准，计算得138万网格数的相对偏差为0.4%，54万网格数的相对偏差为0.9%。3种网格数量计算结果相近，本文模拟研究所用网格数量为138万，并将其计算的舱板热流密度视为额定热流密度。

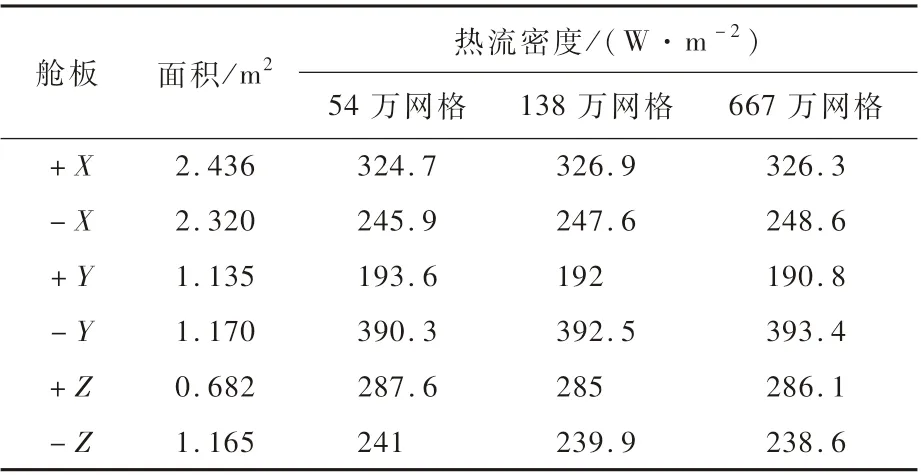
表2 不同网格数下舱板的热流密度Table 2 Heat flux of cabin p lates at various grid num bers

3 模块化设计

本文模块化设计的思想是：将舱板划分成数个相互独立的模块，并对不同模块进行分别热控，以提高舱板温度的均匀度。具体设计过程为：根据各舱板的几何结构及舱板表面热负荷的分布情况对舱板进行初步划分，其目的是使各舱板满足所需的热控要求；对满足条件的划分结果，进行进一步划分，其目的是对初步划分结果进行整合，调整模块的种类和大小，来满足舱板模块化的需求。以该模块划分方法对遥感器模块进行整体模拟，验证最终结果的合理性和有效性。最终模型要满足以下要求：各舱板温度偏差全部保证在0～2 K之间；为方便生产制造，模块形状以矩形为主，且模块种类不得多于30种；为方便拼装连接，各舱板所用模块数量少于30块。

3.1 未模块化设计的舱板温度

根据额定热流密度，计算各舱板未进行模块化设计的温度分布，如图4所示。计算时，各舱板均加载额定热流，但各舱板温度分布呈现出较大差异，＋X、－Y、＋Z三个舱板所受辐射环境单一，舱板各位置热负荷基本相同，温度均匀性较高；－X舱板可分为受到底部钢架直射影响的高温区域和未受到直射影响的低温区域，2个区域温差明显；＋Y舱板受散热板的影响，整体温度呈现出上高下低的分布，最大温差高达10K，温度分布不均匀；－Z舱板由于受到电子学设备舱的影响，中心位置温度较高，并呈环状分布向四周递减。提取与试验中测点位置相同的温度模拟值进行分析，温度偏差在0～2 K之间的点占39.1%，0～1 K之间的占32.6%。与试验数据相对比，模拟温度虽存在一定差异，但总体分布与试验数据基本相同，仅在－X、＋Y和－Z三个舱板出现了较大的温度偏差。

图4 未模块化设计的舱板温度分布Fig.4 Temperature distribution of cabin plates withoutmodularization design

3.2 模块化拼装的舱板温度

采用模块化设计方法对舱板进行划分，经过多次优化整合，确定分块方案如图5所示。根据图4的计算结果可以看出，＋Z舱板温度分布均匀性良好，因此设计时未对＋Z舱板进行分块。所用到模块种类为23，每个舱板所用模块数量小于30块，保证了舱板拼接和工装方便。各模块之间做绝热处理，因此通过调节各模块的加载热流量大小可以将各舱板温度控制在热控要求范围之内。在此方案中，所划分的模块彼此独立绝热，需要通过机械拼装连接在一起，因此称为模块化拼装。

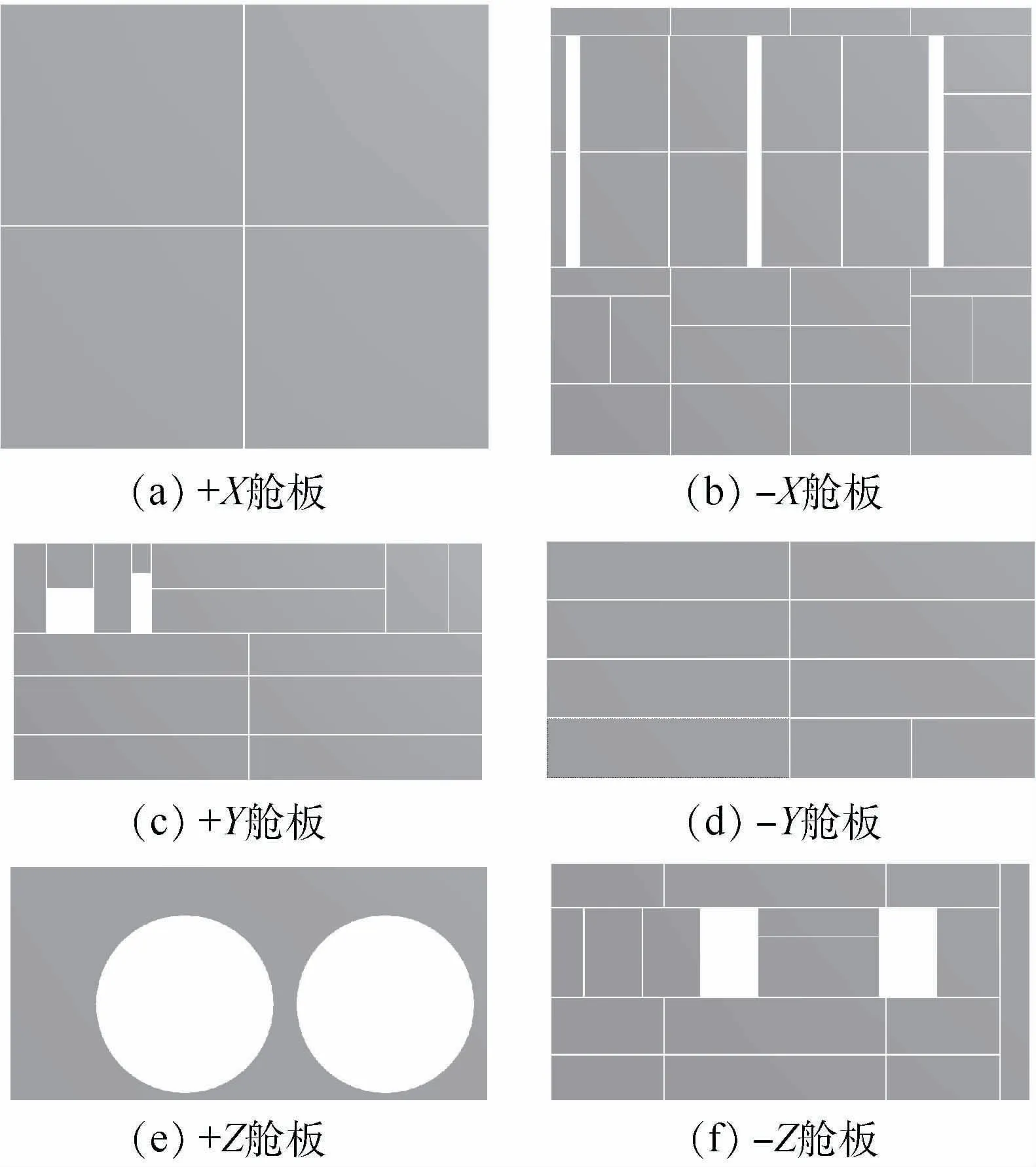
图5 舱板模块化设计方案Fig.5 Modularization design scheme of cabin plates

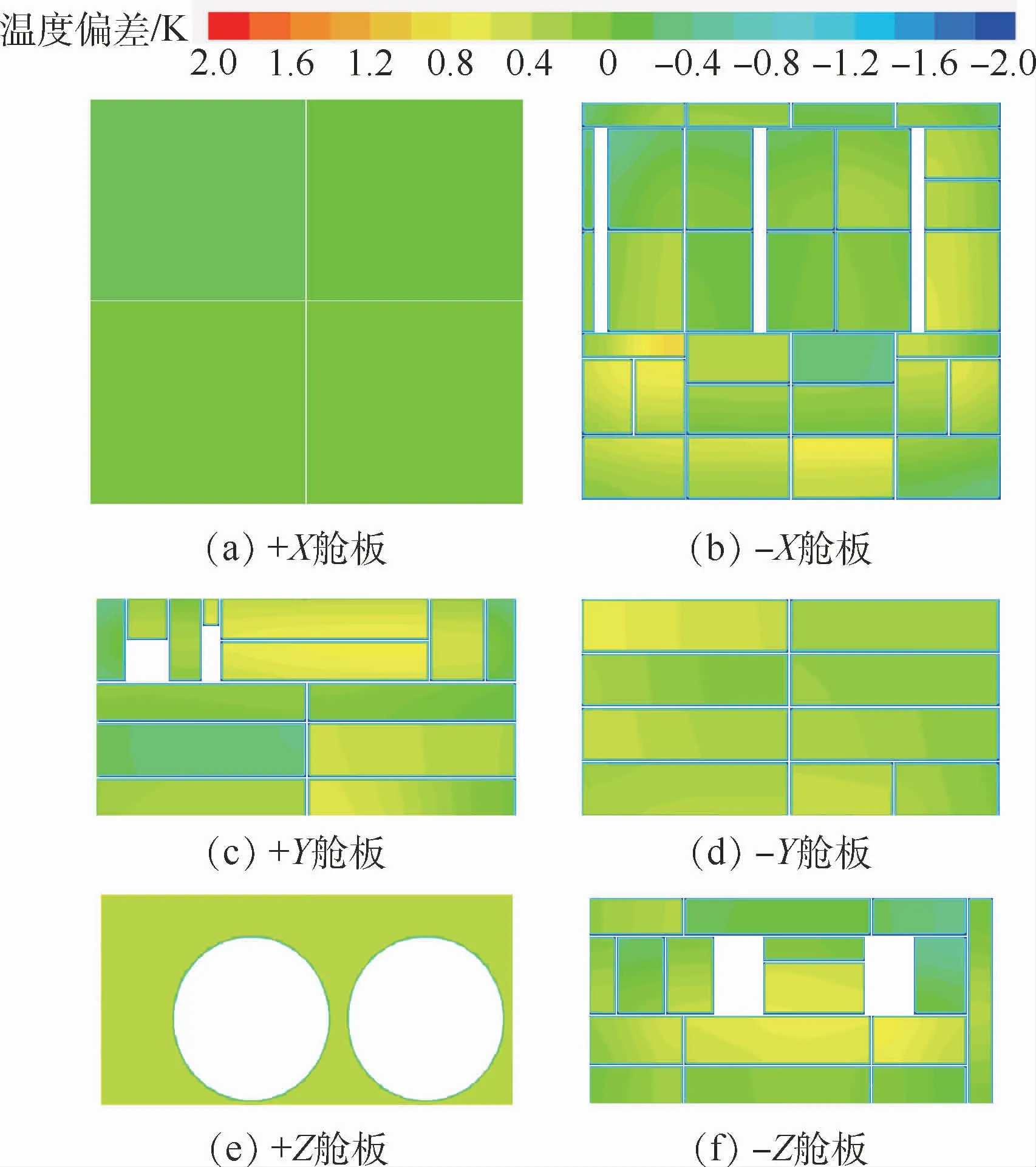
图6 模块化拼装的舱板温度分布Fig.6 Temperature distribution of cabin plates adopting modularization assembly

图6给出了模块化拼装的舱板温度分布，较之图4所示的未模块化设计的情况，舱板温度均匀性有了显著提高，可以满足热控要求，选取第1节环模试验中热电偶的位置做为模拟测点来描述模拟结果，并与试验结果进行对比分析，得温度偏差在0～2 K 之间所占比例由34.8%提升为96.7%，温度偏差在0～1 K 之间所占比例由28.3%提升为93.5%。

3.3 模块化热控的舱板温度

由模块化拼装方案中可以看出，虽然各舱板整体满足所需热控要求，但由于各模块之间相互独立，导致模块间温度存在一定差异。为了消除这种温度偏差，对模块划分方案开展了进一步的优化。由于出现这种温差的原因是模块之间的绝热处理，因此，取消各舱板的独立模块划分处理，但不改变原有加热片的位置和热流量，即只在舱板的不同位置贴上不同功率的加热片来对舱板温度分布进行优化，该方案称为模块化热控。图7为模块化热控的舱板温度分布，选取第1节环模试验中热电偶的位置做为模拟测点来描述模拟结果，发现温度偏差均在0～0.5 K之间，完全满足了热控要求。

图7 模块化热控的舱板温度分布Fig.7 Temperature distribution of cabin plates adopting modularization thermal control

3.4 对比验证

比较3种不同情况下的温度分布，相比于未模块化方案，模块化拼装方案很好地解决了舱板温度分布不均的问题，将舱板温度偏差控制在了0～2 K的范围内；而模块化热控方案将舱板视为一个整体，允许各模块之间换热，进而消除了模块化拼装方案中温度的不连续分布，从而提高了温度均匀性，将温度偏差控制在0～0.5 K以内。符合热控要求的测点比例也由未模块化的34.8%提高到了模块化拼装的96.7%和模块化热控的100%。从安装的角度来分析，模块化拼装方案中需要添加大量安装块；而模块化热控方案中舱板为一个整体，大大降低了安装难度。

试验和2种模块化设计的测点温度与热控要求之间的偏差如图8所示。为了便于比较，运用统计方法对3种方案的数据进行处理，求得各舱板的平均温度偏差Δ和标准温度偏差σ。

式中：xi为各测点的温度；x0为舱板热控温度；n为测点个数。

图8 温度偏差对比Fig.8 Comparison of temperature deviation

表3 舱板温度统计结果Tab le 3 Statistical resu lts of cabin p late tem peratures

舱板温度的对比结果如表3所示。从各舱板的角度来看，模块划分之后大部分舱板温度偏差及均匀性有了显著改善，总体平均温度偏差由试验的0.873 K，降到模块化拼装的0.299 K和模块化热控的0.205K，并且标准温度偏差也在同步降低，说明模块化后舱板温度更接近所需工况温度，且均匀性更好，在相同模块划分情况下，模块化热控的温度分布优于模块化拼装。

4 结 论

本文针对光学遥感器空间环境地面模拟试验中舱板所出现的温度不均匀现象，运用ANSYS软件建立了真空环境中舱板的辐射模型，模拟计算了真空下舱板的温度分布。

对此本文提出了一种基于舱板热流分布的模块划分方法，通过将舱板分成数个形状规则的模块，来提高均匀性。已有的结果显示：模块化拼装方案提高了舱板温度均匀度，但模块间的温度存在一定的差异；而模块化热控方案中将舱板视为一个整体，因此整个舱板温度变化连续。结果表明，模块化拼装可显著提高舱板温度均匀性，测点温度在0～2 K之间所占比例由34.8%提升为96.7%；而模块化热控可得到更优的温度分布，能保证所有测点温度均满足热控要求。

从计算结果可以看出，用模块化设计的方法来改进舱板的温度均匀性是可行的，但不同工装几何结构及表面热负荷的分布都不尽相同，同样的模块难以应用于其他工装，而模块化思想则具有普适性，即根据舱板的几何结构特征及表面热负荷的分布情况，对舱板进行模块划分。

目前，在环模试验中对舱板的热控方式主要为在舱板外表面贴加热片的方式，通过改变流入加热片的电流大小来控制加热功率，本文仅研究在该加热方式下的舱板温度分布，未考虑不同加热模式对舱板温度分布的影响，在后续会对该内容进行进一步研究。