土工参数概率特性的贝叶斯优化估计

徐志军 张健 肖昭然 刘军

摘要：足量精确的土工参数测试数据是计算其均值和标准方差的关键，在工程实际中，受到各种不确定性因素的影响，获得足量精确的数据较为困难。基于数理统计方法，建立土工参数数据优化处理模型，将数据优化处理为“好数据”和“一般数据”，剔除离散性较大的数据;利用随机加权法将数据量较小的“好数据”和“一般数据”进行加权处理。最后利用贝叶斯方法对土工参数概率分布的均值和标准方差进行优化估计。通过算例分析表明：贝叶斯优化后的标准方差大大降低;贝叶斯优化后的概率分布均值与“好数据”的均值相差很小，但与一般数据的均值和所有数据的均值相差较大。证明了贝叶斯优化后的均值和标准方差更接近工程实际，由此估计出的工程安全性更加科学合理。

关键词：土工参数;概率特性;贝叶斯优化;均值;标准方差

中图分类号：TU413.4

文献标志码：A

doi：10.3969/j.issn.1000- 1379.2019 .01. 022

土工参数的概率特性是岩土工程可靠度研究的基础，参数数据的准确性和数据样本的容量决定了概率分布特性[1]。在实际工程中，受各种不确定性因素的影响，如取样的扰动、试验误差、测量工具和方法的不稳定、土层本身固有的变异性等，要获得足量准确的土工参数数据是非常困难的[2-4].因此在岩土工程中需要对收集到的土工參数测试数据进行优化处理，在此基础上研究其概率分布。黄天朗等[2]提出了利用勒让德多项式和第二类切比雪夫多项式拟合参数概率分布，并给出了区间取值方法。王新等[3]利用随机加权法，提出了小样本情况下岩土参数概率分布的多项式拟合方法。骆飞等[4]分析了岩土参数小样本t分布法区间估计存在的问题，利用Bootstrap法对岩土参数数据进行重构，得出了数据区间估计和点估计。孟庆山等[5]利用概率理论和数理统计理论给出了土工参数的统计方法，并将其应用到工程实际。宫凤强等[6]基于信息扩散原理，给出小样本下岩土力学参数概率密度函数拟合方法。徐志军等[7]分析了利用经典概率分布（譬如正态分布、对数正态分布和贝塔分布等）拟合岩土参数概率分布的不足，采用最大熵原理和随机加权法给出了岩土参数概率密度函数的求解方法。

以上研究主要集中在概率拟合精度和小样本拟合方法上，这些研究未考虑参数数据“质量好坏”的问题。本文基于数理统计方法，建立土工参数数据优化处理模型，将数据优化处理为“好数据”和“一般数据”，剔除离散性较大的数据：利用随机加权法将数据量较小的“好数据”和“一般数据”进行加权处理：最后利用贝叶斯方法对土工参数概率分布的均值和标准方差进行了优化估计。

1 土工参数数据的处理方法

在岩土工程中，工程勘测通过不同手段如现场试验、室内模型试验、钻探等可获得土的物理参数数据（孔隙比、塑性指数、液限等）和力学参数数据（抗剪强度、压缩模量等）。这些参数数据在统计中受到各种不确定性因素的影响，导致统计数据具有较大的变异性。不确定性主要有土层本身固有的空间变异性、取样的扰动、试验误差、尺寸效应和时间效应等，因此需要对参数数据进行优化处理，剔除那些离散性较大的数据。

“坏数据”的离散性较大，在实际工程中可能受到各种因素的影响，是“错误的”，会对计算结果造成较大误差，因此在计算中需要剔除“坏数据”。

根据式（4），若得到的“好数据”很少，则由此得到的概率统计特性就不准确。为了解决这一问题，首先利用随机加权法将“好数据”加权为大样本，统计得到加权后的概率特性：然后利用贝叶斯方法对加权后的数据概率特性进行优化。

2 基于随机加权法的贝叶斯优化

郑忠国[9]详细论证了随机加权法可以有效地解决小样本问题。因此，本文利用式（9）对处理后的土工参数“好数据”进行加权处理，得到概率分布的均值、方差和变异系数。

2.2 贝叶斯优化方法

贝叶斯统计是基于已有数据计算条件概率的统计方法。在岩土工程中，将已有的土工参数数据作为待分析数据，其概率分布为先验分布。利用概率理论对先验概率分布进行更新和校正。假设统计的土工参数

3 实例分析

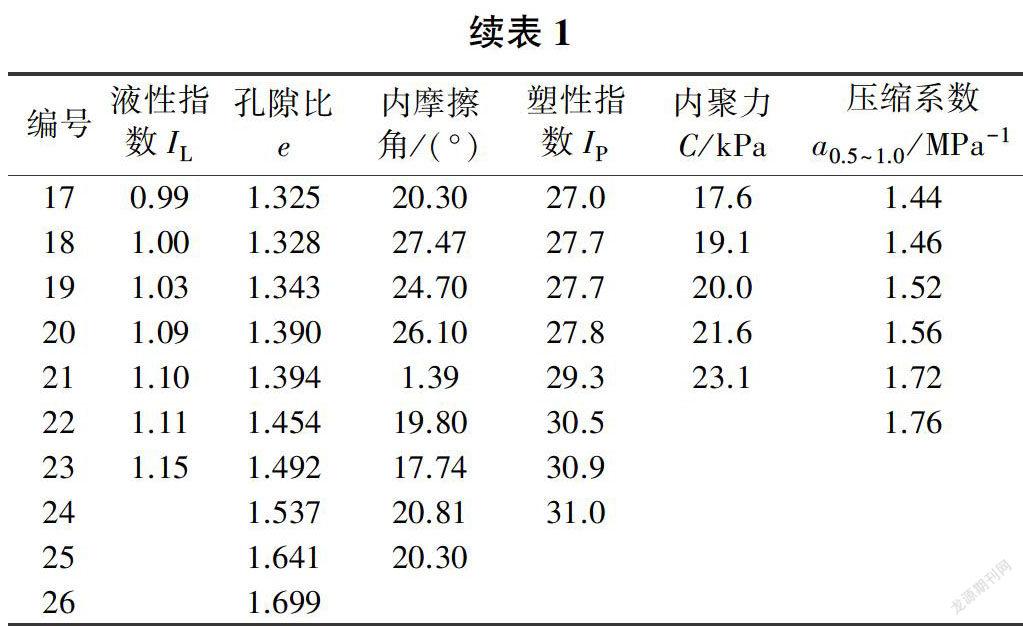
文献[2]收集了10组土工参数数据，本文选用其中的6个参数数据，见表1。文献[2]通过分析得出这些数据的精确性不高，拟合出的概率特性不够准确，需要对这些数据进行优化处理。

利用式（4）对表1中的统计数据进行优化处理，处理结果见表2和表3。其中内摩擦角25号数据，内聚力1、17号数据，压缩系数17号数据的偏差因子大于等于0.5，离散性较大，对计算结果会造成较大误差，在统计中应剔除。

由文献[2]可知，液性指数、孔隙比、内摩擦角、塑性指数、内聚力和压缩系数分别服从正态分布、正态分布、正态分布、对数正态分布、贝塔分布、贝塔分布。由概率统计理论可知，概率分布的均值和标准方差是其两个最重要的统计参数。利用本文提出的随机加权法（加权系数为60）和贝叶斯优化方法对每个土工参数的均值和标准方差进行优化处理，优化结果见表4。由表4可以看出，优化后数据的标准方差小于好数据的标准方差，好数据的标准方差小于所有数据的标准方差，而一般数据的标准方差比所有数据的标准方差大。譬如，对于内摩擦角，贝叶斯优化后的数据、好数据、所有数据和一般数据的标准方差分别为1. 72、2.58、5.12、6.26，相差较大，说明贝叶斯优化后数据的离散性降低，数据更接近工程实际。另外，优化后的数据均值与好数据的均值相差很小，但与所有数据和一般数据的均值相差较大。因此，经过优化后的数据更加精确可靠。

4 结论

为了处理土工参数数据“质量好坏”问题，建立了优化处理模型，利用随机加权法和贝叶斯方法研究了土工参数数据概率特性的估计方法，通过研究得到以下结论：

（1）本文提出的数据处理方法可将统计的土工测试数据中离散性较大的数据剔除，大大减小计算误差。

（2）贝叶斯优化后数据的离散性大大降低，数据更接近工程实际。优化后的数据均值与好数据的均值相差很小，但与所有数据和一般数据的均值相差较大。因此，经过优化后的数据更加精确可靠。

参考文献：

[1] PHOON K K，CHING Jianye. Risk and Reliability inGeotechnical Engineering[M]. New York： Taylor &Francis， 2015： 339-433.

[2] 黄天朗，官凤强，伍婷玉，小样本岩土参数概率分布的正交多项式推断方法[J].工程力学，2017，34（8）：85-95.

[3] 王新，黄磊群，随机加权法辅助小样本岩土参数概率分布的边坡稳定性分析[J].公路工程，2017，42（3）：131-136.

[4]骆飞，罗强，蒋良潍，等，小样本岩土参数的Bootstrap估计及边坡稳定分析[J].岩石力学与工程学报.2017，36（2）：370-379.

[5]孟庆山，雷学文，土工参数的统计方法及其工程应用[J].武汉冶金科技大学学报（自然科学版），1999，22（4）：414-417.

[6]宫凤强，李夕兵，邓建，小样本岩土参数概率分布的正态信息扩散法推断[J].岩石力学与工程学报，2006，25（12）：2559-2564.

[7] 徐志军，肖昭然，蔡正银，等，基于随机加权熵的岩土参数概率分布的拟合研究[J].防灾减灾工程学报，2014，34（sl）：6-10.

[8]

ANG A H S，‘rANG W H.Probability Concepts in Engineer-ing： Emphasis on Applications to Civil and EnvironmentalEngineering. 2nd Edition[ M]. New York： John Wiley&Sons，2006：106-110.

[9] 郑忠国，随机加权法[J].应用数学学报，1987，10（2）：247-253.