基于支持向量机的注浆锚杆锚固参数反分析

孙长宁 苏立君 朱秦 李丞

摘要：注浆锚杆极限抗拔力一般通过现场试验进行测定，但在锚固工程数值模拟分析过程中，所需的锚固参数（如注浆体的黏结强度和摩擦角）很难直接确定。提出了一种基于支持向量机的注浆锚杆锚固参数反分析方法，即利用锚杆极限抗拔力反分析锚固参数。选取锚杆极限抗拔力作为实测目标，结合均匀试验和支持向量机建立锚固参数与实测目标之间的映射关系，通过蒙特卡洛法枚举大量锚固参数样本，利用上述已建立的映射关系计算枚举的锚固参数样本，得到对应目标的计算值。在此基础上，根据目标实测值筛分得到符合条件的目标计算值对应的锚固参数，并通过关于注浆锚杆的模型案例说明了该方法的可行性。

关键词：注浆锚杆;锚固参数;支持向量机;反分析：极限抗拔力

中图分类号：U456.3

文献标志码：A

doi：10. 3969/j .issn. 1000- 13 79.2019.01. 032

目前，注浆锚杆被广泛应用于边坡、隧道工程中，其最重要的参数为极限抗拔力，一般通过现场试验确定。许多学者对注浆锚杆的极限抗拔力进行了理论研究。Li等[1]根据锚杆拉拔试验，提出了拉拔荷载作用下注浆锚杆的力学分析模型：Cai等[2]考虑到锚杆与岩体变形协调，建立了注浆岩石锚杆的轴力预测理论模型，Shahin等[3]采用神经网络方法预测了锚杆的极限抗拔承载力：魏新江等[4]考虑锚杆注浆体界面强度和注浆体岩土体界面强度对全长黏结式锚杆抗拔力的影响，以及浆体与岩土界面的塑性区发展，推导得出了全长黏结式锚杆的抗拔力计算公式：邓宗伟等[5]基于统一强度理论和极限平衡原理，结合预应力锚索破裂面的形状，推导出了预应力锚索极限抗拔承载力的计算公式：贺建清等[6]基于改进的Mohr - Coulomb强度准则，从塑性力学极限分析上限定理出发，利用虚功原理推导得出了岩石锚杆极限抗拔承载力的计算公式。然而，在注浆锚杆锚固工程数值分析中，需要提前确定相关锚固参数（如单位长度上注浆体的刚度、黏结强度和摩擦角等），而不是极限抗拔力[7]，但关于注浆锚杆锚固参数的研究相对较少。John等8]给出了一些关于上述注浆锚杆锚固参数的经验公式，但沒有给出注浆体摩擦角的近似公式：Li等[9]基于注浆锚杆的极限抗拔力，利用二分法对注浆岩石锚杆的锚固参数进行了反分析，但该方法需要事先确定参数初值，其对锚固参数最终分析结果影响较大。

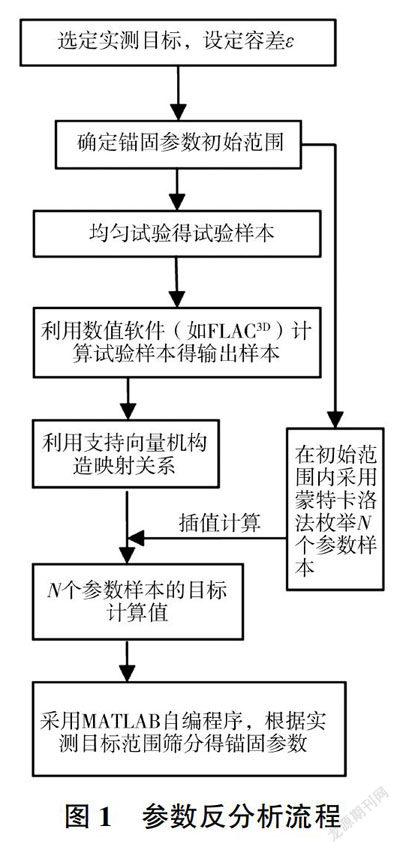
针对上述问题，本文提出了一种基于支持向量机的注浆锚杆锚固参数反分析方法，即利用锚杆极限抗拔力反分析锚固参数。选取锚杆极限抗拔力作为实测目标，结合均匀试验和支持向量机建立锚固参数与实测目标之间的映射关系，通过蒙特卡洛法枚举大量锚固参数样本，利用上述映射关系计算锚固参数样本，得到对应实测目标的计算值，并根据目标实测值，筛分得到符合条件的目标计算值对应的锚固参数。

1 基于支持向量机的注浆锚杆锚固参数反分析

2 算例分析

为了证明本文方法的可行性，选用文献[7]中的注浆岩石锚杆拉拔试验案例，根据锚杆极限抗拔力，利用该方法反分析注浆锚杆的锚固参数。所选案例的FLAC3D数值模型尺寸为0.4 mx0.7 mx0.4 m.模型内部设置0.5 m长的锚杆，其余单元为岩体，模型边界围压为2 MPa。岩体与锚杆的相关参数见表1。

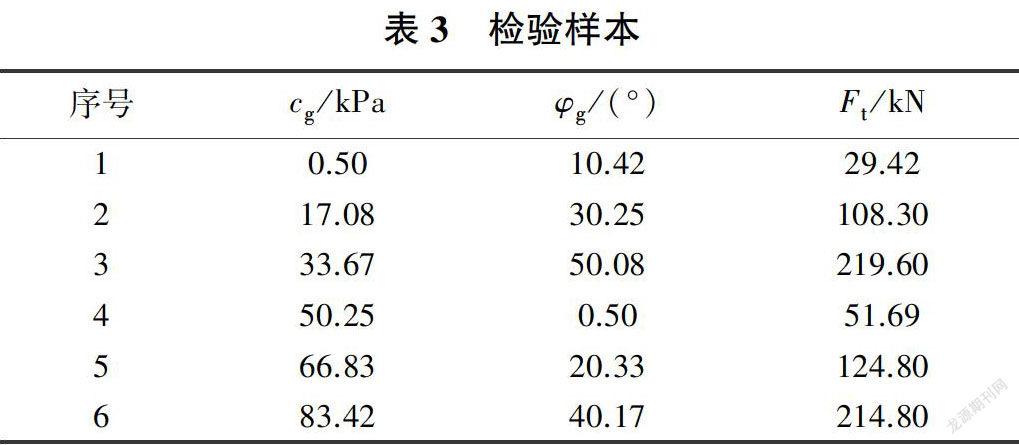
选择锚杆的极限抗拔力作为实测目标，将注浆体黏结强度（c）和摩擦角（φ）作为待定锚固参数。根据试算或现有资料，确定锚固参数初始范围：c为[0，100 kPa]，φ为[0，50°]，将上述两个参数作为随机参数。针对上述随机参数，将其分为14个水平，即2个参数14个水平，采用MATLAB自编程序得到均匀表U14（142），从而得到14组参数的输入样本。根据上述FLAC3D软件建立的力学模型，计算输入样本进而得到对应的输出样本（即锚杆的极限抗拔力），见表2。重复上述步骤，获得6组检验样本，见表3。

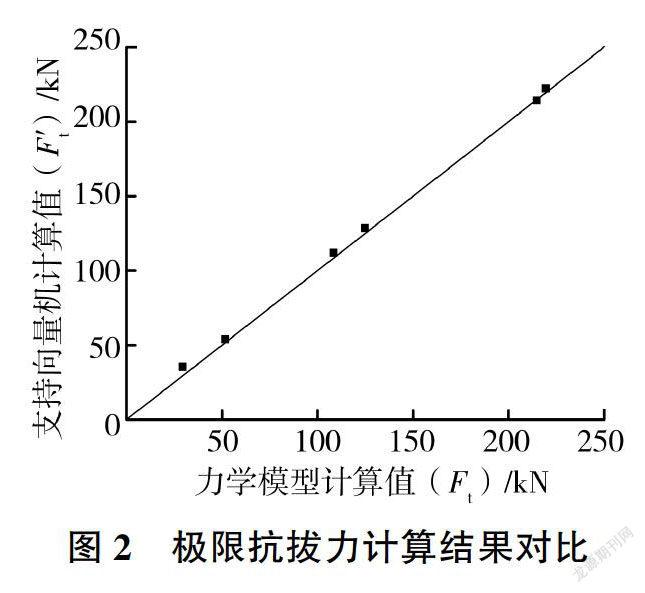
根据表2中的训练样本，采用支持向量机建立注浆体黏结强度、摩擦角与锚杆极限抗拔力之间的映射关系，均方根误差小于0.001。利用上述已建立的映射关系计算表3中检验样本的6组参数，得到对应的极限抗拔力预测值，与表3中力学模型计算得到的极限抗拔力结果进行对比，见图2。由图2可以看出，两种方法得到的结果接近，因此上述基于支持向量机建立的映射关系是有效且可用的。

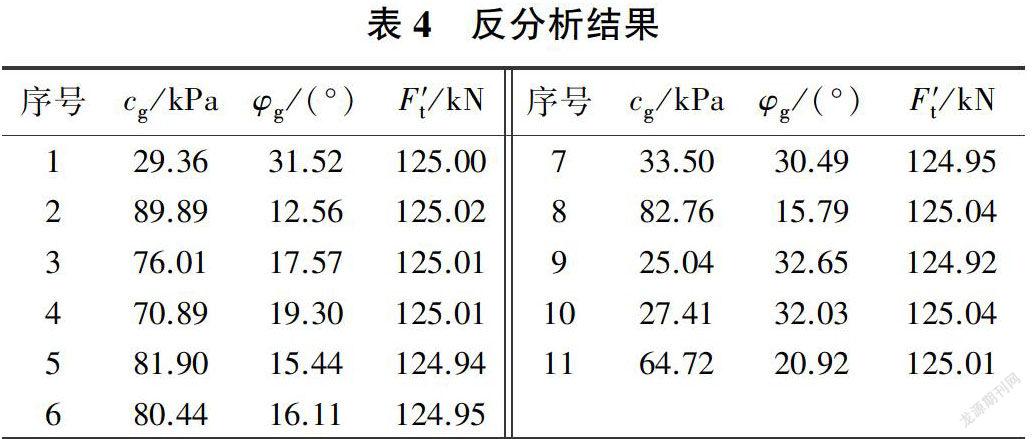
设注浆锚杆极限抗拔力的现场试验实测值为125kN，允许容差ε=0.1 kN，则目标实测值为[124.9，125.1]。根据待定锚固参数的初始范围，利用蒙特卡洛法枚举10 000组随机样本，采用上述已建立的映射关系计算每组随机样本，进而得到对应的10 000组输出样本，即锚杆极限抗拔力计算值。在此基础上，结合目标实测值范围，筛分出该范围内的目标计算值以及对应的锚固参数，见表4。

由表4可知，反分析结果不是唯一解，而是两个锚固参数的多种组合，主要原因是目标函数为1个方程、2个未知数，从数学求解的角度看，其结果为多组解。表4反分析结果不一定是注浆体的真实锚固参数，但每一组解均满足锚杆极限抗拔力的计算值等于现场实测值，因此可以替代真实锚固参数，解决数值模拟过程中锚固参数取值的问题。

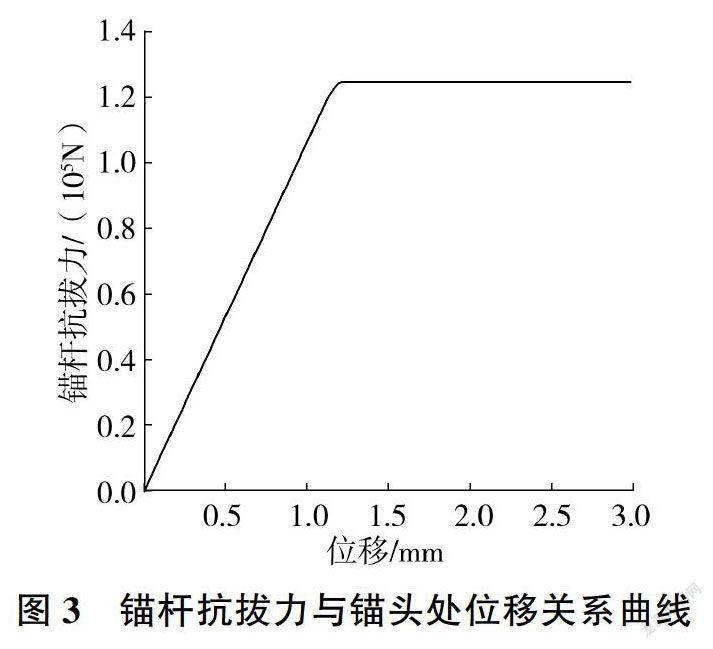
根据现有资料和参数的物理意义可知，注浆体的锚固参数φ约为30°[9]。根据表4，当锚固参数取c=29.36 kPa.φ=31.52°时，将其输入到上述用FLAC3D建立的数值模型中进行分析，结果见图3和图4。由图3可知，锚杆抗拔力随锚头处位移的增大而增大，当锚头处位移增大到一定程度时，锚杆抗拔力达到最大值，并且趋于平稳，此时即为锚杆的极限抗拔力。由图4可知，注浆锚杆距离锚头越近，轴力越大;注浆锚杆距离锚头越远，轴力越小。

3 结语

提出了一種基于支持向量机的注浆锚杆锚固参数反分析方法。利用该方法可以根据锚杆的极限抗拔力试验值反分析注浆体的锚固参数，从而便于注浆锚杆加固工程数值模拟过程中锚固参数的确定。同时，通过一个简单案例说明了该方法的可行性。通过引入支持向量机智能算法，建立样本之间的映射关系，进而快速计算大量参数样本，提高了参数反分析的效率。提出的参数反分析流程具有通用性。针对其他具体工程的参数反分析问题，建立相应的力学模型，选择合适的实测目标（如位移）和待定参数（如土体抗剪强度指标），也可利用上述流程进行参数反分析。

参考文献：

[1] L1 C，STILLBORG B.Analytical Models for Rock Bolts[ J].Intemational Journal of Rock Mechanics and MiningSciences， 1999， 36（8）：1013-1029.

[2]

CAI Y，ESAKI T，JIANG Y.An Analytical Model to PredictAxial Load in Grouted Rock Bolt for Soft Rock Tunnelling[J]. Tunnelling and Underground Space Technology， 2004，19（6）：607-618.

[3] SHAHIN M A， JAKSA M B.Neural Network Prediction ofPullout Capacity of Marquee Cround Anchors[J].Computersand Geotechnics， 2005， 32（3）： 153-163.

[4]魏新江，张世民，危伟，全长粘结式锚杆抗拔力计算公式的探讨[J].岩土工程学报，2006，28（7）：902-905.

[5]邓宗伟，冷伍明，李志勇，等，基于统一强度准则的预应力锚索极限承载力计算[J].岩石力学与工程学报，2007，26（6）：1138-1144.

[6] 贺建清，肖兰，张文勇，等，基于改进的Mohr- Coulomb强度准则下岩石锚杆极限抗拔承载力计算[J].岩土力学，2016，37（9）：2484-2488.

[7] Itasca Consulting Group， Ir'ic. FLAC3D： Fast Lagran～;ian A—nalysis of Continua in 3 Diruensions[M].Minneapolis： MN，2006： 95-108.

[8] JOHN C M， VAN DILLEN D E.Rockbolts：a NewNumerical Representation and Its Application in Tunnel De-sign[ C]//The 24th US Symposium On Rock Mechanics（USRMS）. Texas： American Rock Mechanics Association，1983： 66-76.

[9] LI Bin， TAIYUE Q， WANG Z，et al.Back Analysis ofGrouted Rock Bolt Pullout Strength Parameters from FieldTests[J].Tunnelling and Underground Space Technology，2012， 28： 345-349.

[10] 方开泰，均匀设计及其应用（Ⅱ）[J].数理统计与管理，1994，13（3）：52-55.

[11] SONG Zhigang， SONG Jie. Reliability Analysis of CompartmentFire by Improved Response Sruface Method[C]//Proceedings ofthe Eleventh International Symposium on Structural Engjneering.Beijing： Science Press，2010： 1271-1276.

[12]赵洪波，冯夏庭，位移反分析的进化支持向量机研究[J].岩石力学与工程学报，2003，22（ 10）：1618-1622.

[13] 许传华，任青文，周庆华，基于支持向量机和模拟退火算法的位移反分析[J].岩石力学与工程学报，2005， 24 （22）：4134-4138.

[14] 许传华，任青文，郑治，等，索风营水电站地下洞室岩体力学参数的位移反分析[J].岩土工程学报，2006， 28 （11）：1981-1985.

[15] 李波，徐宝松，武金坤，等，基于最小二乘支持向量机的大坝力学参数反演[J].岩土工程学报，2008， 30（11）： 1722-1725.