中小学教师教学领导力理论模型的验证
2019-09-10吴晓英
吴晓英



摘 要: 教师教学领导力理论模型的构建与验证是教师群体明晰教学领导力的内涵与结构进而提升与发展教学领导力的前提基础和关键起点,采用质性与量化相结合方法构建所得的教师教学领导力理论模型由“愿景创设力”“教学决断力”“教导执行力”“沟通激励力”“教学人际力”和“结果驱动力”等六维度构成,探索性因素分析表明该模型的信、效度良好;为进一步验证模型的跨样本稳定性,采用交互验证的方法对理论模型进行验证性因素分析和信、效度检验。结果显示教师教学领导力理论模型具有很高的信度和效度以及跨样本的稳定性和代表性,能为后续教学领导力的实践应用提供实证基础。
关键词: 中小学教师;领导力;教师教学领导力;理论模型;验证性因素分析
中图分类号:G451 文献标识码:A 文章编号:1674-7615(2019)01-0025-08
DOI:10.15958/j.cnki.jywhlt.2019.01.006
在以“立德树人”为根本任务,发展“核心素养”为教育目的的背景下,提升教师的核心素养是实现教育目的的根本路径;而教师教学领导力是教师综合素养具备的最佳体现,也是教师自身专业发展的内在要求和学校课堂教学效能实现的关键,因而构建并验证教师教学领导力理论模型的跨样本稳定性和代表性,多维度明晰教学领导力的内涵与结构,是教师深入认知自身和提升教学领导力的发展所需,其对教师群体教学核心素养的发展价值重大。
一、问题提出
结合理论文献[1-2]与教学实践的启示,研究建构了具有六维核心能力的教师教学领导力理论模型(见图1),并以模型为基点编制了教师教学领导力测度问卷,经过探索性因素分析得出,由“教学品格”为内在核心,“愿景创设力”“教学决断力”“教导执行力”“沟通激励力”“教学人际力”和“结果驱动力”六维能力为外在核心的教师教学领导力理论模型具有数据上的实证支持;为深入探究教师教学领导力理论模型是否具有跨样本稳定性和科学性,需要在探索性因素分析的基础上对模型进行验证性因素分析,以进一步验证教师教学领导力六维模型外在核心是否具有跨样本的稳定性和科学性。
二、研究设计
(一)测量工具
以自编的由“愿景创设力”“教学决断力”“教导执行力”“沟通激励力”“教学人际力”和“结果驱动力”等六维度构成的“教师教学领导力量表”作为测量工具,按照分层抽样原则向中小学教师进行抽样调查;采用的探索性分析工具是SPSS20.0,验证性分析工具为Amos21.0。
(二)研究对象及方法
运用“教师教学领导力量表”测量工具在全国的华东地区(山东、安徽)、华南地区(广东、广西)、华北地区(北京、山西)、西北地区(新疆、青海)和西南地区(贵州、四川、云南、重庆)各地州市的各类型与层次的中小学校教师实施大样本调查,采样方法为网上问卷与实地发放纸质问卷相结合的方式。问卷共发放3700份,收回3531份,回收率95.43%。剔除无效问卷,分析问卷共有3482份(其中网上回收有效问卷539份),问卷有效率为98.61%。
为更好探究量表结构,运用交叉验证方法,以样本来源地区为依据把有效的总问卷随机分成两组(每组1741份),一组(称为“探索卷”)用于对问卷结构进行探索性因素分析,另一组(称为“验证卷”)用于对探索出的结构模型进行验证性因素分析,以验证探索性因素分析所得的“教师教学领导力理论模型”的结构稳定性,限于篇幅,这里只呈现验证性因素分析结果。
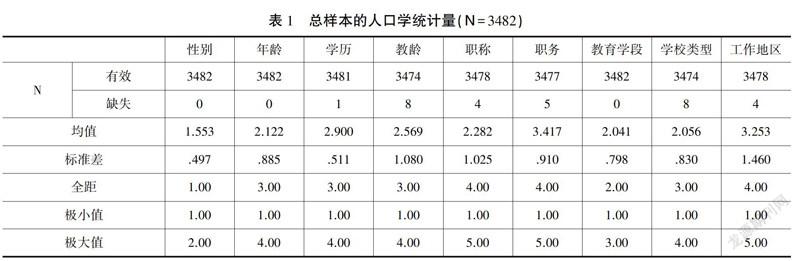
(三)总样本的人口学统计量
总样本的人口学统计量见表1所示。有效样本为3482人,人口學统计量的类别有9个,即性别、年龄、学历、教龄、职称、职务、教育学段、学校类型和工作地区,其中学历、教龄、职称、职务、学校类型和工作地区题项存在缺失值,分别为1、8、4、5、8和4人。
三、“教师教学领导力量表”的验证性分析结果
探索性因素分析偏向于理论的产出而非理论架构的检验;而验证性因素分析偏重于检验假定的观察变量与潜在变量间的关系。为验证前期经过探索性因素分析所得到的“教师教学领导力六维结构模型”是否具有跨样本的稳定性,需对总样本中的另一份样本(验证卷,N=1741)进行验证性因素分析,以对量表结构进行检验。
(一)教师教学领导力理论模型的竞争比较
一般来说,量表可能包含几种相异的结构维度,为检验量表在数据上是否具有最佳的指标,可运用竞争模型来实现多模型间的比较,进而验证出最佳的量表结构维度。竞争模型比较技术最大的优势在于,允许有测量误差的情况下对观察变量与潜变量、潜变量与潜变量之间的关系进行验证。[3]
以教师教学领导力的一阶六因素模型为基准模型,然后依据基准模型中维度间相关水平的大小以及相应理论的指导,将其中某两个或以上相关水平偏高的因素层面合并,从而得到如下三个可用于比较的竞争模型。
●竞争模型 1 = 五维模型
即五维模型:教学执行力=(教导执行力+沟通激励力);愿景创设力;教学决断力;教学人际力;结果驱动力。
●竞争模型 2 = 四维模型
即四维模型:教学影响力=(教导执行力+沟通激励力+教学人际力);愿景创设力;教学决断力;结果驱动力。
●竞争模型 3 = 三维模型
即三维模型:愿景决断力=(愿景创设力+教学决断力);教学影响力;结果驱动力。
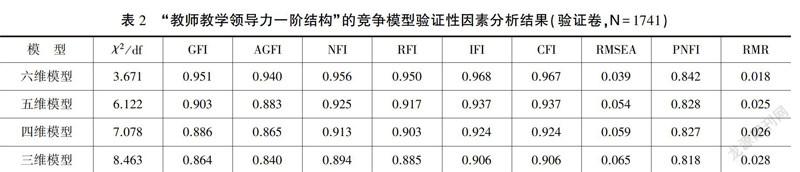
绝对、增值和简约适配度指数是竞争模型比较的主要检验指标。依据模型的适配标准,主要以“绝对适配度指数”(卡方自由度比值χ2/df、GFI、AGFI、RMR、RMSEA),“增值适配度指数”(NFI、RFI、IFI、CFI)和“简约适配度指数”(PNFI)等10个指数作为评价指标,结果见表2所示。
表2的数据表明,六维模型的数据较其它3个竞争模型的适配度更理想。χ2/df为3.671,达到小于5的适配标准;GFI值为0.951;NFI为0.956;RFI为0.950,达到完美指标;IFI为0.968;CFI为0.967,均大于0.90,拟合指数优良;RMSEA值为0.039,小于0.050;PNFI值为0.842,大于0.50,上述10个指标均优于其它三个模型。可见,教师教学领导力六维模型是竞争比较中最理想的,故选择“六维度教师教学领导力模型”是有据可依的。
(二)一阶验证性因素分析结果
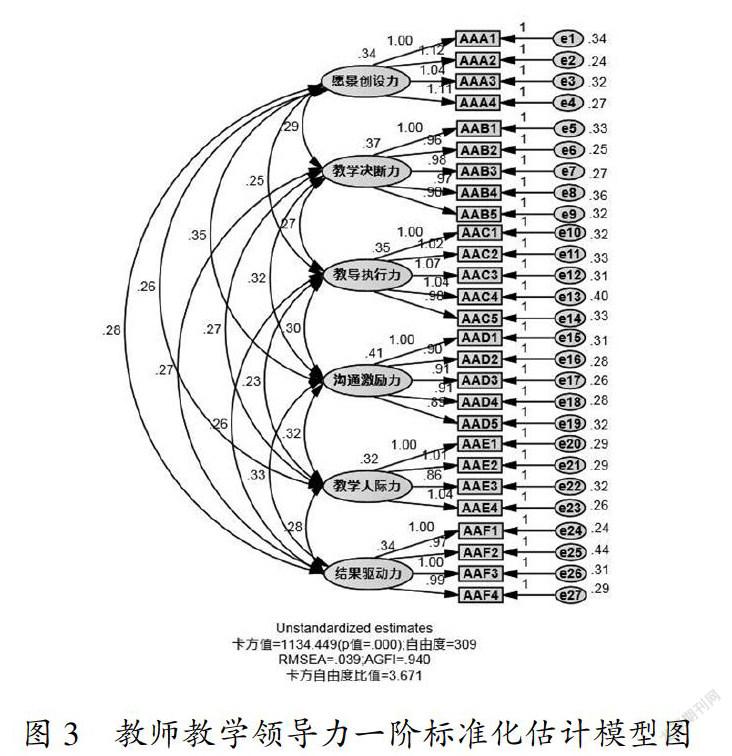
为探究“教师教学领导力”一阶模型的结构效度,检验经过探索性分析得出的“六维教师教学领导力”一阶模型的样本适配情况,研究进行了一阶模型的验证性因素分析,得到的非标准化和标准化模型估计值分别见图2和图3所示。
图2是非标准化估计值模型图,无负的误差方差,表明模型的界定没有问题;图3是标准化估计值模型图,卡方值为1134.449,自由度为309,RMSEA为0.39,AGFI为0.940,卡方自由度比值为3.671;因素负荷量介于0.65至0.80之间;潜在变量之间的相关系数值介于0.70至0.95之间,呈中高度相关,表示这六个潜在层面之间可能有一个更高阶的共同因素,即教师教学领导力。
模型内每个估计参数是否都达到显著水平是检验模型内在质量的重要指标之一,表中所估计的69个参数均达到显著水平,表示模型的内在质量理想。估计参数标准误还可用来检验假设模型是否有违反辨认规则。如果估计参数标准误很大或有负的误差方差存在,表示假设的理论模型有可能违反辨认规则。上述69个估计参数的标准误均很小(介于0.010至0.039),且没有出现负的误差方差,显示假设模型没有违反辨认规则。图2中数据表明,除6个固定参数外,其余估计参数都达到显著水平(P<0.05),t值的绝对值大于1.96且达到0.001的显著水平。将上述各测量指标变量的因素负荷量、信度系数、测量误差变异量整理成教师教学领导力一阶模型的参数估计摘要表,如表3所示。
首先,在一阶验证性因素分析中,潜在因素“愿景创设力”的四个测量指标的因素负荷量分别为0.706、0.796、0.729、0.781;“教学决断力”五个测量指标的因素负荷量分别为0.729、0.762、0.755、0.700、0.691;“教导执行力”五个测量指标的因素负荷量分别为0.720、0.723、0.749、0.697、0.708;“沟通激励力”五个测量指标的因素负荷量分别为0.758、0.742、0.752、0.745、0.713;“教學人际力”四个测量指标的因素负荷量分别为0.726、0.725、0.653、0.755;“结果驱动力”四个测量指标的因素负荷量分别为0.766、0.649、0.723、0.731;27个测量指标的因素负荷量介于0.649至0.796之间λ值皆在0.50和0.95之间,表示基本适配指标理想。
其次,在探索性因素分析中,各构念或层面的信度系数是“内部一致性α系数”;而验证性因素分析中,则以“组合信度”作为模型潜在变量的信度系数,可作为模型内在质量的判别准则,其值在0.60以上,表示模型的内在质量理想。“愿景创设力”的组合信度系数值为0.840,“教学决断力”为0.849,“教导执行力”为0.843,“沟通激励力”为0.860,“教学人际力”为0.807,“结果驱动力”为0.810,它们的组合信度系数值均大于0.60,表明模型的内在质量极佳。
再次,平均方差抽取量(ρv或AVE)的数值愈大,表示测量指标愈能有效反映其共同因素构念的潜在特质。由表3发现,“愿景创设力”为0.568,“教学决断力”为0.530,“教导执行力”为“0.518”,“沟通激励力”为0.551,“教学人际力”为0.512,“结果驱动力”为0.516,六个潜在变量的AVE值都大于0.50,表示模型的内在质量理想。
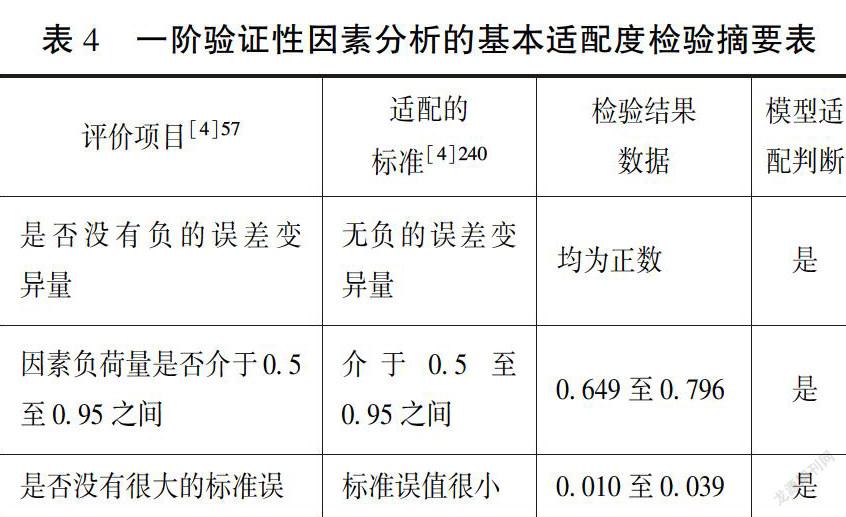
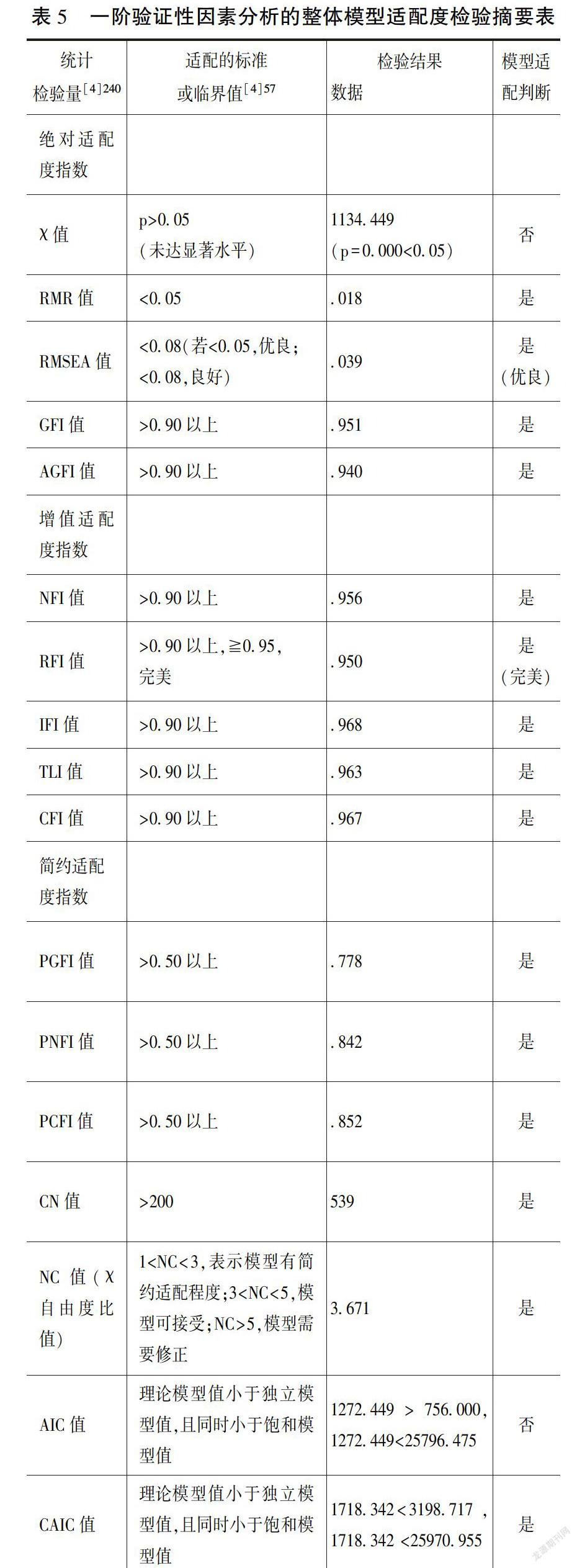
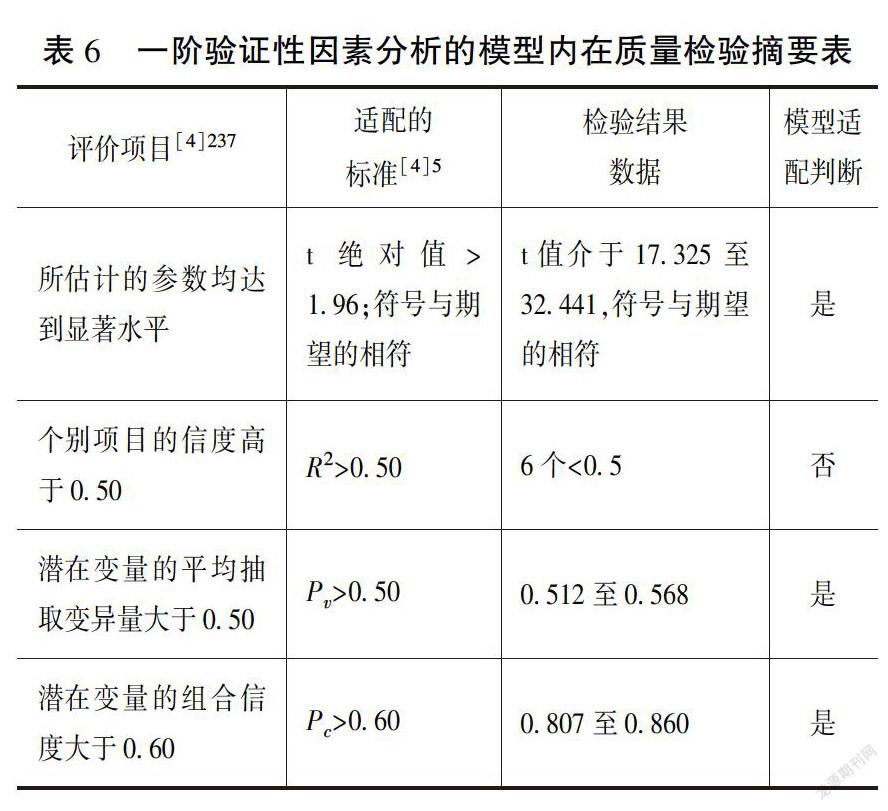
最后,“教师教学领导力结构量表”一阶验证性因素假设模型检验的模型契合度评价结果摘要如表4至表6所示。
从表4至表6中得知“教师教学领导力结构量表”CFA模型检验结果如下:
首先,“教师教学领导力量表”一阶验证性因素分析模型的基本适配度指标均达到检验标准,这表明估计的基本适配指标良好,无违反模型的辨认规则。[4]57
其次,在整体模型适配度方面,绝对、增值与简约适配指标统计量中,所有适配指标值均达模型可接受的标准,自由度为309时,卡方值为1134.449,p=0.000<0.05,拒绝虚无假设。卡方值对受试样本的大小非常敏感,样本数愈大,则卡方值愈容易达到显著,导致理论模型遭到拒绝的概率愈大;[4]41学者Rigdon也认为,χ2值受估计参数及样本数影响很大,因而使用真实世界的数据来评价理论模型时,χ2统计通常实质帮助不大;[5]而且模型参数愈多,所需的样本数就愈多,若是在一个模型大而样本小的状态下,χ2检验的问题就会更严重。[4]41估计参数越多,影响假设模型的变因越多,假设模型适配度不佳的情形会越明显,而当样本数较大时,往往造成卡方值变大,此时很容易拒绝虚无假设,[4]472因而χ2值的显著性仅仅作为一个参考的指标,还需要参考其他指标综合考虑。
从表5看出,除了χ2值的显著性之外,所有的其他关键指标都符合,并达到良好以上标准,因而表示研究者提出的理论模型与实际数据可以契合。整体而言,“教师教学领导力正式量表”一阶验证性因素分析模型与实际观察数据的适配情况良好。
再次,在内在质量检验方面,有6个测量指标的信度系数虽未达0.50的标准,但接近0.50。所估计参数的t值介于17.325至32.441,t绝对值>1.96,符号与期望的相符,所有待估计的参数均达到显著水平;潜在变量的平均抽取变异量值介于0.512至0.568之间,大于0.50的标准;潜在变量的组合信度值介于0.807至0.860之间,达到理想的信度水平。故模型的内在质量较为理想。
(三)二阶验证性因素分析结果
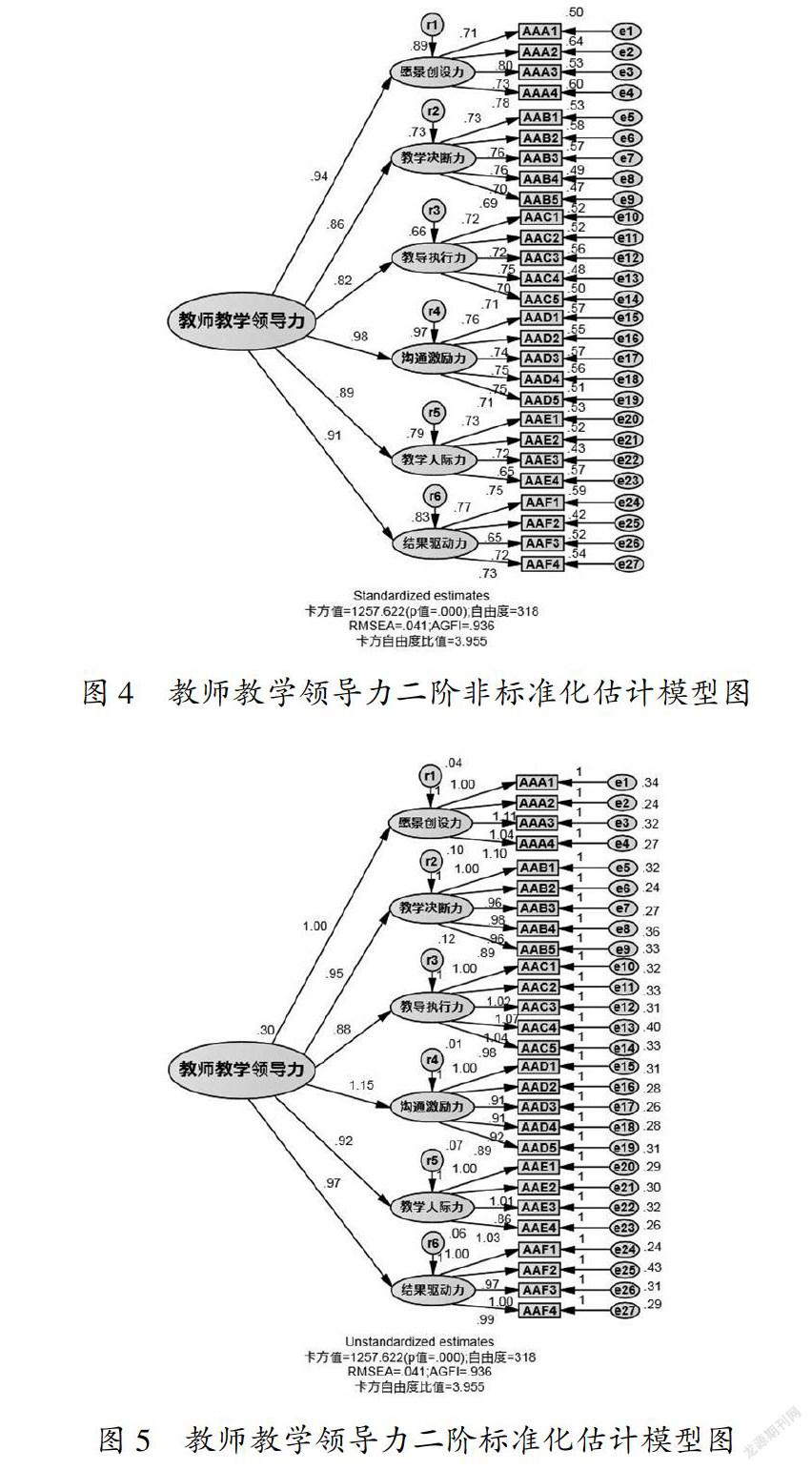
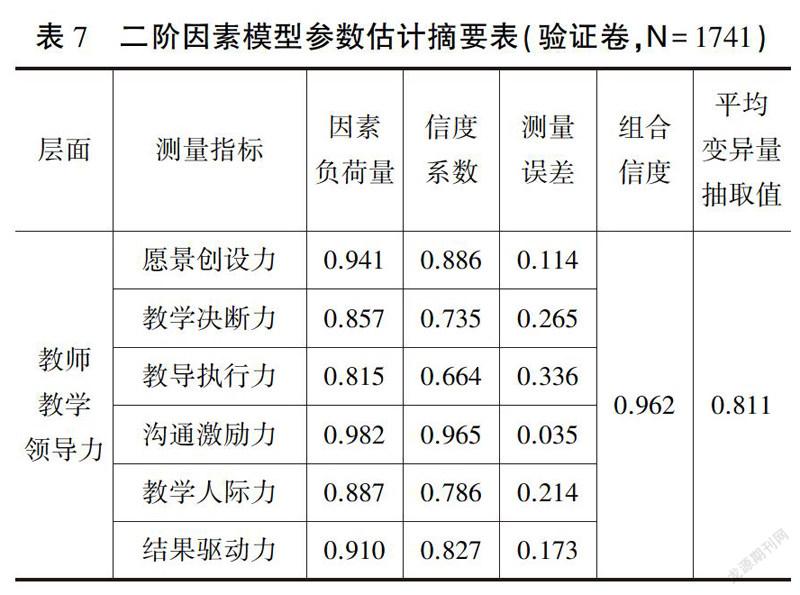
以上“教师教学领导力一阶模型”的验证性因素分析发现:一阶模型中六个潜在层面间有中高度相关,且一阶验证性因素分析模型与样本数据可以适配,因而可能这六个潜在层面间拥有一个更高阶的因素构念:即教师教学领导力。因而本研究再对样本二进行“教师教学领导力二阶模型”的验证性因素分析。其非标准化估计模型如图4,标准化估计模型如图5所示。
圖4教师教学领导力的非标准化估计模型图,卡方值为1257.622;自由度为318;RMSEA等于0.41小于0.5;AGFI等于0.936大于0.90;卡方自由度比值等于3.955(小于5的标准);并且没有出现负的误差变异量,表示模型界定没有问题;六个初阶因素构念与27个观察变量均为内因变量,因而无法估计其方差。
图5是教师教学领导力二阶标准化的模型估计图,其卡方值为1257.622;自由度为318;RMSEA值为0.41(小于0.50的标准);AGFI等于0.936(大于0.90的标准),卡方自由度比值为3.955(小于5的标准)。六个初阶因素构念的因素负荷量分别为0.94、0.86、0.82、0.98、0.89和0.91,均大于0.71;其信度指标值分别为0.89、0.73、0.66、0.97、0.79、0.83,大部分达到理想的指标值。
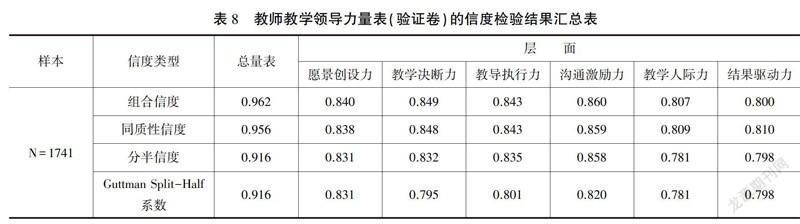
二阶因素的验证性输出结果汇总如表7所示,所有测量指标的因素负荷量介于0.815至0.982,都大于0.5;信度系数介于0.664至0.965,大部分都高于0.50;测量误差介于0.035至0.336;“教师教学领导力”的组合信度为0.962,大于0.60的标准;而且平均变异量抽取值为0.811,大于0.50的标准,因而“教师教学领导力二阶模型”的内在质量极佳。
结构方程模型的验证适配标准需要从“基本适配度”“整体模型适配度”和“内在质量检验”三方面来综合判别。首先,从“基本适配度”来看,二阶因素模型的误差变异量均为正数,因素负荷量均在0.5以上,标准误值很小(介于0.028至0.041之间),表明二阶因素模型完全达到基本模型适配度的标准;其次,从“整体模型适配度”来看,其绝对适配度指数:χ2值为1257.622,RMR值为0.020(<0.05),RMSEA值为0.041(<0.05,优良),GFI值为0.946,AGFI值为0.936(>0.90),大部分指标都达到了适配的标准,因而本量表的整体模型适配度良好。就增值和简约适配度指数而言,增值适配度指数(>0.90):NFI值为0.951,RFI值为0.946,IFI值为0.963,TLI值为0.959,CFI值为0.963,都均大于0.90;简约适配度指数(>0.50):PGFI值为0.796,PNFI值为0.862,PCFI值为0.872,CN值为499(>200),NC值(χ2自由度比值)为3.955(3
四、讨论与建议
(一)“教师教学领导力二阶模型”的信度检验
信度是指测验或量表工具所测得结果的稳定性以及一致性,量表信度越大,则其测量标准误越小,它关系到测量结果的可信度和有效性。本研究采用组合信度、同质性信度、分半信度和Guttman Split-Half 系数四个指数作为参照,对验证卷样本进行信度检验,所得结果如表8所示。
表8是验证卷样本六层面和总量表的信度结果汇总表,由数据看出,量表六层面的组合信度值介于0.800至0.860之间,大于0.50的标准;分半信度值介于0.781至0.858之间;Guttman Split-Half 系数值介于0.781至0.831之间,均达到理想的信度标准;总量表的组合信度值为0.962,同质性信度为0.956,分半信度为0.916,Guttman Split-Half 系数为0.916,均达到非常理想的信度水平,多种信度的数据都充分证明本研究的验证卷样本量表具有相当理想的内在信度。
(二)教师教学领导力量表的效度检验
量表效度主要指量表是否确实能够测量出其所欲测量的特质或功能程度。[6]这里主要检验量表的内容、收敛、结构和区分效度。
1内容效度
内容效度指一个测量实际测到的内容与所要测量内容之间的吻合程度。[7]量表开发始终扎根教师教学领导力已有的基础理论,密切联系基础教育学校教学发展的新理念和变化趋势、客观、科学地反映中小学教师教学领导力的典型特征、认知现状与观点,并在相关教育学、领导学专家的指导下来进行量表设计、维度命名和题项内容的确定等,同时还进行了探索性、验证性因素分析、相关分析与信度分析等,所得数据都支持:“教师教学领导力结构量表”具有相当好的内容效度。
2收敛效度
收敛效度是指测量相同潜在特质的题项或测验会落在同一个因素够面上,且题项或测验间所测得的测量值之间具有高度的相关。[4]这里主要从AVE值和确认性因子分析方法两方面来检验量表的收敛效度。首先,从AVE值(一般的判别标准是大于0.50)来看,量表各维度的AVE值在0.512至0.568之间(见表3),均超过0.50。其次,从确认性因子分析方法来看,全部测量题项的标准化负荷位于0.649至0.796之间,均超过0.50的可接受水平,并全部通过t检验,均在p<0.01的水平上显著。上述双方面的数据都证实本量表的收敛效度良好。
3结构效度
结构效度指一个测量实际所要测到的理论结构或特质程度。[8]研究通过多个竞争模型比较和验证性因素分析,各项拟合指标均达到理想状态,绝对适配度指数:RMR值=0.020,GFI=0.946,AGFI=0.936,RMSEA=0.041,均优于建议值。增值适配度指数:NFI=0.951,RFI=0.946,IFI=0.963,TLI=0.959,CFI=0.963,也优于建议值。简约适配度指数:PGFI=0.796,PNFI=0.862,CN=499,χ2/df=3.955等,所有题项均全部通过t检验,均在 p<0.01 的水平上显著,因此表明教师教学领导力结构测度量表具有很好的结构效度。
4区别效度
区别效度是指构面所代表的潜在特质与其他构面所代表的潜在特质间低度相关或有显著的差异存在。[4]467这里也从两方面来评估量表的区别效度:第一,量表全部题项都通过筛选,均不存在严重跨因子负荷的现象;第二,采用Amos的检验做法,即通过在每两维度的测量模型之间进行“未限制模型”和“限制模型”的卡方值差异显著性比较。教师教学领导力量表有六个维度,因而两两模型之间的关系共有15对,由于篇幅限制,结果汇总表这里不再展示;由嵌套模型比较摘要表显示:教师教学领导力总量表的各潜在构面中,两模型间的自由度差异为1,卡方差异量值介于443.696至707.779之间,卡方差异量的显著性检验的概率值p=0.000<0.05,均达到0.05显著水平,表示未限制模型与限制模型两测量模型有显著不同;与限制模型相比之下,未限制模型的卡方值显著较小,表示教师教学领导力总量表的六个因素构念间具有良好的区别效度,27个题项反映出六个不同的因素构念,因而由“愿景创设力”“教学决断力”“教导执行力”“沟通激励力”“教学人际力”和“结果驱动力”等六维度构成的教师教学领导力量表的区别效度佳。
总之,研究以教师教学领导力六维结构模型为基础,提取出能较好反映教师教学领导力典型特征的题项,并编制初始测量问卷,经过严格的问项筛选、内容润色、项目分析、探索性因素分析以及信、效度检验等试测分析后,得到内容简练、结构适宜、信度高的教师教学领导力正式量表;然后在全国华东、华南、华北、西北和西南地区的各地州市选择不同层次的中小学教师进行正式调查;经过对大样本数据的探索性因素分析(限于篇幅,这里略)和验证性因素分析,如多模型的竞争比较、信度与内容效度、结构效度、收敛效度、区分效度等项目的检验,最终验证了内、外在质量等各项指标均优佳的教师教学领导力理论模型的科学性与结构的稳定性。
参考文献:
[1] Alig-Mielcarek,J.M.A Model of School Success:Instructional Leadership,AcademicPress,and Student Achievement[D].The Ohio State University,2003:48.
[2] Alig-Mielcarek,J.M.and Hoy,W.K.Instructional Leadership:Its nature, meaning, and influence[A].In:W.K.Hoy & C.Miskel(Eds.) Educational leadership and reform.Greenwich,CT: Information Age Publishers,2005:29-54.
[3] 候杰泰,温忠麟,成子娟.结构方程模型及其应用[M].北京:教育科学出版社,2004:167-174.
[4] 吴明隆.结构方程模型:Amos的操作与应用(第2版)[M].重庆:重庆大学出版社,2010.
[5] Rigdon,E.A necessary an sufficient identification rule for structural equation models estimated[J].Multivariate Behavioral Research,1995(30).
[6] 楊国枢,文崇一.社会及行为科学研究法[M].重庆:重庆大学出版社,2006:269.
[7] 凌文辁,方俐洛.行为与心理测量[M].北京:机械工业出版社,2003:231.
[8] 黄光杨,原霞.教育统计与测量评价新编教程[M].上海:华东师范大学出版社,2013:77.
(责任编辑:蒲应秋)
