“好数”问题新解

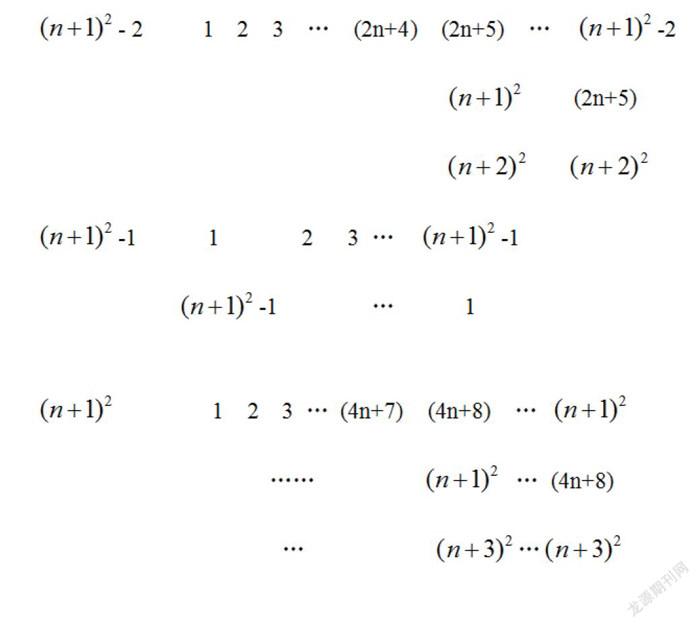
【摘 要】好数有多种理解。

理解一：好数，意思是两个整数，它们的积能被和整除，就称为一对“好数”。

理解二：好数：数ab（a>0，b>0）ab与ba最大公因数不为1，ab即是好数

理解三：好数：对于自然数N，如果找到自然数a和b，使得N=a+b+ab，则N称为“好数”

在此就不一一例举了

【关键词】好数;枚举;筛选;列表解法

引言

朱华伟教授和钱展望教授在他们的专著《数学解题策略》一书第三章枚举与筛选的第35页[例3.5]中，讨论了所谓“好数”问题：

如果存在1，2，…，n的一個排列a1，a2，…an，使得k+ak（k=1，2，…，n）都是完全平均数，则称n为“好数”。问在集合{11，13，15，17，19}中，哪些是“好数”，哪些不是“好数”，说明理由！

书中通过对集合中的5个元素逐一枚举，进行讨论，结论是：11不是“好数”，即13，15，17，19都是“好数”！

二位教授在本章问题第16题（见该书第44页）还把“好数”问题一般化：

如果存在1，2，…，n的一个排列a1，a2，…an，使k+ak（k=1，2，…，n）都是完全平均数，则称n为“好数”，问在正整数集合中，哪些是“好数”，哪些不是“好数”，并说明理由。

针对作者编著的《数学解题策略》一书，二位教授还编写了一本习题指导书，即《数学解题策略问题解答》，书中第40页，第41页对第16题给出详细的讨论和证明（笔者注：在问题解答一书中，相应问题的编号为15，不是16，经查，原来漏掉第14题的解答，从而把第16题当成第15题）。

笔者看了此题的解答后，觉得对一般化的讨论，较为抽象，因此在下文里，给出一种列表解法，同时纠正解答中的一处疏忽。

原解答第一句说“正整数集中只有{1，2，4，6，7，9，11}不是‘好数’”。经笔者演算，其中的正整数9是“好数”，兹列表如下：

k    1    2    3   4   5    6     7   8    9

ak     8    2   6    5   4    3     9   1    7

k+ak    32   22   32   32   32   32   42   32   42

所以，正整数集中只有6个数不是“好数”。

为讨论其他的正整数都是“好数”，先用列表法列出3—24之内的相应排列，分两个表，见附件1。

为了讨论一般的情况，不妨考察一下整数段52-62的排列特点，如下：

25=52       1   2   3 … 23   24   25

… 25   24

72    72

由于23已证明是“好数”，所以由左的排列法25也是“好数”。

26           1   2   3  …  22   23   25   26

…  26   24    23

34           1   2   3  …  14   15   16  …  32   33   34

…         34   33  … 17   16   15

现在可以讨论整数段n2-（n+1）2的情况，仿列表明示（鉴于前面的讨论，现可设n≥6）：

由于假设n≥6，不难断定，上列表中的大小顺序排列是没有问题的，且其中最小的划红波浪线的数2n+4>16，避开了非“好数”的出现！

这就证明了，除六个不是“好数”之外，其他的都是“好数”！

参考文献

[1]朱华伟，钱展望《数学解题策略》2版、科学出版社，2015.1（走进教育数学/张景中主编）

[2]朱华伟，钱展望《数学解题策略问题解答》2版、科学出版社

作者简介：高宁（1962-）女，云南省民族中等专业学校，本科，中专高级讲师，研究方向为中专数学、教育学、职业生涯规划