一题多解 开阔思路

陈剑青

对有些题适度进行一题多解既能调动学生积极性，又极大提高教学有效性，尽可能的让学生进行联想，去感知题中蕴含的基本思想。在此，我举一教学过程实例，会考复习在即，一天班上一位同学拿来一题请教老师，题目如下：

看起来好象没什么错，但学生忽略了基本不等式对取等号成立的条件。

教师为学生回顾x2+y2≥2xy当且仅当“x=y时等号成立”。实质上①式和②式取等号时不可能同时成立，学生恍然大悟。

启示1：教师在教学中展示数学概念、结论、应用的形成发展过程积极探索新的途径和方式，促进学生数学学科核心素养的发展。基本不等式教学重点是应用数形结合的思想理解基本不等式，并从不同角度探索基本不等式的证明过程，难点是用基本不等式求最大值和最小值。在解决实际问题中着重引导学生领会基本不等式√ab≤（a+b）/2（a，b≥0）成立时的三个限制条件（简称一正二定三相等）在求解实际问题中的作用。

那到底如何解呢？题目分析如下：

启示2：在教学中应在理解教材、把握教材的基础上，根据教学目标、所带学生的需要和学习特点做适度的延伸或对内容做适当的调整。

方法二：

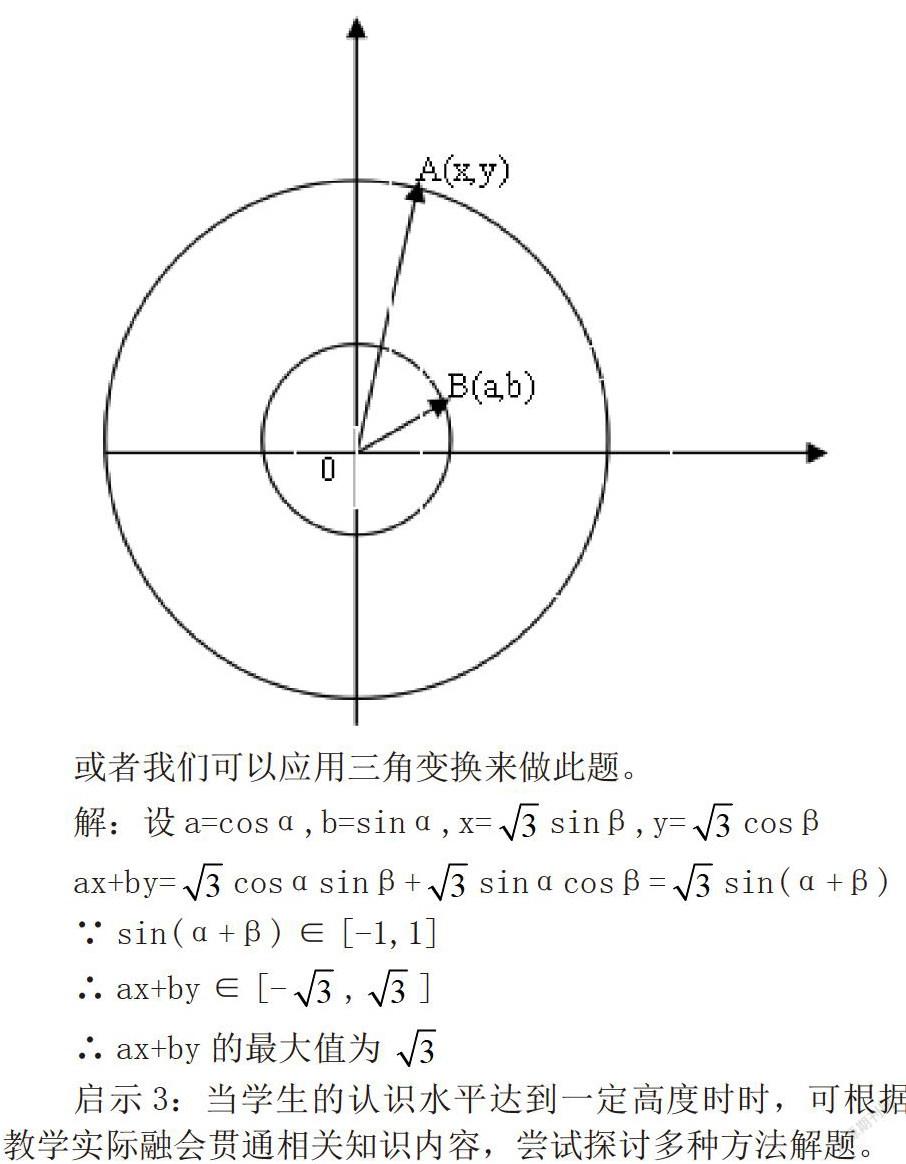
题中两个方程为圆的方程，因此利用圆的方程思想，数形结合思想及向量思想来做此题。

启示3：当学生的认识水平达到一定高度时时，可根据教学实际融会贯通相关知识内容，尝试探讨多种方法解题。

总结本题：

方法一、基本不等式的应用要注意取“等号”的条件。

方法二、向量是近代数学中重要和基本的数学概念之一，有深刻的几何背景，是解决几何问题的有力工具。本题通过平面向量的数量积运算把不等式问题通过数型结合转化为向量的运算体系。

方法三、利用三角知识，使学生体会三角恒等变换的基本思想和方法，发展推理能力和运算能力使三角恒等变换其到工具性作用。

反思与感悟：首先学生是数学学习的主体，一题多解应以学生能力为出发点，以学生发展为终点，在尊重学生现有思路的前提下帮助学生学会知识技能思想方法，更关注如何引导学生学会学习会思考会应用，使学生能够实现可持续发展和终身学习的基本保证。其次数学教学是思维的教学，在一题多解教学中，尽可能多的让学生进行联想，类比，归纳和概括等活动，反思它們的联系和区别，感知其中蕴含的基本思想，从而提高学生学习数学的兴趣。

参考文献

[1]《普通高中数学课程标准》（2017年版）人民教育出版社

[2]《数学必修5教师教学用书》人民教育出版社