建立数学模型 提升学生思维

卢佳

摘 要：最近在计算教学中认真学习“教学目标评价一致性”，发现原来一年级的教学中可以渗透的数学思想方法有这么多，例如最常见的数形结合、转化等，没想到在计算教学中还可以渗透数学模型的思想方法。

关键词：数学模型 思想方法 计算教学 一一对应 合作探究 总结提升

正文：

以前一说起数学思想方法，感觉这是高年级的事情，一年级的学生哪知道什么数学思想方法，最近在计算教学中认真学习“教学目标评价一致性”，发现原来一年级的教学中可以渗透的数学思想方法有这么多，例如最常见的数形结合、转化等，没想到在计算教学中还可以渗透数学模型的思想方法。

上学期读过王永春《小学数学思想方法》一书，当时对于数学模型这种思想方法还比较陌生，这次又深入阅读了一下，知道了“数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构。”

这几天我在教学“求比另一个数多几（少几）”一课时，重点对学生进行了数学模型思想的渗透。“比另一个数多几（少几）”的问题，借助学生在生活中经常对两种物体的个数进行比较，面对实物能判断哪种实物的个数多，哪种实物的个数少，哪种实物比哪种实物多几或少几的知识经验为基础，来教学求两数相差多少的实际问题。

一、复习引入，奠定模型基础。

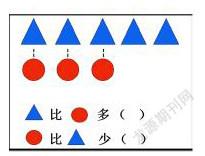
上課伊始，我就出示了一组图片，在教学中有意识地把抽象的数学思想方法一点一滴地渐渐融入具体的、实在的数学知识中，通过观察、操作、思考等活动，使学生逐步积累对这些数学思想方法的初步的直觉认识。首先让学生感受一一对应的数学思想，体会一一对应的优点，并渗透数形结合思想，让学生一眼看出谁多说少，为后面进行画图的操作学习和求两数相差多少的实际问题作了很好的铺垫。

二、合作探究，建立直观模型。

在复习之后，让学生先从以前的画一画比较的方法入手，建立解决“比另一个数多几（少几）”问题的直观模型。

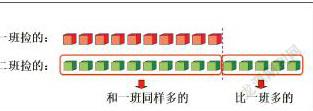
利用大问题“二班比一班多捡了多少个易拉罐？”引导学生，在动手之前，引导学生动脑来想“想一想你想用什么图形来表示一班捡的，画几个？二班呢？怎样画才能清楚的比较出两个班的多少？”让学生明确画的方法和要求，并借助画图，组内交流，归纳方法，建立模型，根据学生回答，引导学生用一一对应的方法排列，并通过数形结合，真正理解分成的哪两部分，为什么用减法，减去哪部分。

接着让学生自主迁移，了解“一班比二班少捡了多少个

与“二班比一班多捡了多少个”是同一个问题，只是说法不同，沟通联系，提升方法，并利用儿歌来帮助学生记忆，建立直观模型。

两数比多少，

先把大数找，

去掉同样多，

多几（少几）就知道。

最后用大问题“三班捡的易拉罐比矿泉水瓶少多少个”来提升学生思维，进一步巩固直观模型。

三、总结提升，建立方法模型。

独立解决大问题“二班比一班少捡了多少个矿泉水瓶？”，然后回顾总结，引导归纳：解决的问题有什么相同的地方？是怎样解决的？让学生发现这些题目都是求一个数比另一个数多几或者少几，都是用减法计算的，而且都是用大数减去小数，让学生建立这类题目的方法模型。

总之，这节课通过“画一画、比一比、想一想、列算式、说算理”等活动，自主探究“求一个数比另一个数多几”的解决方法和算理，再迁移方法，水到渠成地解决“怎样求一个数比另一个数少几”的问题，让他们亲历“操作——思考——交流——概括”的全过程，培养学生自主学习和迁移推理能力，渗透数学模型思想，放手让学生由两位数加一位数和整十数推想两位数减一位数和整十数的算理和算法，培养学生的推理能力，让学生质疑互动，培养学生的问题意识和合作交流的能力，由学具操作提升算法并进行沟通，突出算理和算法的有效结合，渗透数形结合和转化的思想，从画图到计算，逐步脱离情境，进一步抽象出解决一个数比另一个数多几或者少几问题的方法模型，从而最终实现算法模型的有效构建。

参考文献：

黄瑛玮. 借助几何直观 提升数学思考能力——以“求比一个数多（少）几”的问题解决为例[J]. 数学学习与研究， 2014（22）：98-98.