基于学生理解水平 进行适切教学设计

倪乃忠

摘 要：教学设计应该基于学生的理解层次、水平，学生对“两三位数除以一位数”运算的理解是有不同层次的。本文将学生在未进行课堂教学前对“两三位数除以一位数”的理解由低到高分为直观水平、程序水平、抽象水平和形式水平四个层次，进行分类研究，找到课堂教学的最佳切入点，寻找可以借助的学生原有知识框架。按照学生的理解水平，进行合理的教学的教学设计。从而，更好地解决造成学生错误增加的算理与算法沟通的问题。

关键词：教学设计;理解层次;分类研究

一、问题提出

《新课标》强调：“对数与代数学习的评价，应主要考察学生对概念、法则及运算的理解与运用水平”。义务教育教材除了较好地落实大纲精简繁难计算的要求外，还把教学的重点放到了让学生较好地理解算理上。

两三位数除以一位数是除法竖式计算的一次重要的扩展。一方面是理解代数思想、体验函数思想、理解实数系统、进行多项式除法等诸多后续学习的重要基础，不得不学;另一方面又由于除法竖式教学占有往往需要占用较多教学时间，且教学效果一般，学生错误较多，给教与学都带来了很大的挑战，成为小学数学教学中我们不得不直面的问题。

从学生的实际情况出发，对课堂进行有效的教学设计是课程实施的重要环节。本文以“两三位数除以一位数”的课堂教学时间为基础，探讨如何基于学生的理解水平，适切进行教学设计。通过本研究，期待解决以下问题：

1.学生对两三位数除以一位数运算算理理解达到什么层次？

2.学生达到该理解水平的主要影响因素是什么？

3.通过上述问题的探索，基于学生的理解水平，我们应该如何进行适切的有效教学设计？

二、理论背景

（一）相关研究成果综述

杭师大教育心理学教授巩子坤老师领导的研究团队提出有理数运算理解的四种类型：直观理解、程序理解、抽象理解、形式理解。基于这样的理解层次论，结合自己的教学实践，开展本次课题的相关研究。

（二）“三位数除以一位数”的内涵界定

本研究中“两三位数除以一位数”指乘法口诀表外的两位数除以一位以及三位数除以一位数的运算。对于“两三位数除以一位数”运算的理解即为对以上运算内容的算理与算法的理解。

（三）“两三位数除以一位数”理解水平分层界定

结合国内外研究成果，主要依据巩子坤教授提出的有理数运算理解的四种类型，本研究将“两三位数除以一位数”理解水平界定为以下四个层次：

（1）直观水平：能够用直观图像或现实情境来给出正确答案。

（2）程序水平：按照除法竖式运算法则算出正确的答案。

（3）抽象水平：会计算，并结合算式，用语言描述结果的合理性。

（4）形式水平：会计算，并结合已知的规则、规律，用逻辑推理的形式，证实运算结果的合理性。

三、研究过程

（一）研究对象

鉴于研究的代表性（选取学校位于城郊结合部，正在飞快融入大城市）和方便性，以所在学校作为研究对象。学校学生数学整体水平处于该地区中等偏上水平。从这所学校所有年级中选取三年级（进行两三位数除以一位数教学之前）全体共 105名学生。为了纵向对比了解，寻求学生对“两三位数除以一位数运算”随着年龄与知识增长而产生的理解层次水平的变化，又在这所小学选取了四年级全体 105 名（三年级时学习过两三位数除以一位数）学生作为对比研究对象。

（二）研究工具

1.问卷调查。对没有进行任何兩三位数除以一位数教学的三年级的学生，进行问卷调查。问卷要求尝试解决以下问题：用自己喜欢并且熟练地方式，比如用文字解释、画直观图展示、用算式计算等尽可能多的方法阐述计算结果的正确性。整个过程，阐述地越详细越好。问卷调查一共三个习题。

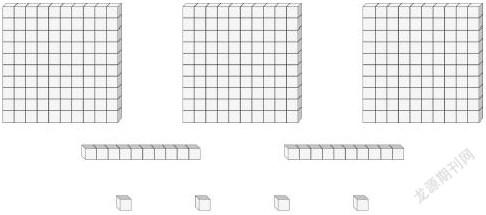
（1）这些小立方体要分装到 3 个盒子里，每个盒子里需要装几个小立方体？

（2）一共有 72 人参加会议，分为 6 个分会场，平均每个场地需要容纳多少人？

（3）648÷6 你会计算吗？

2.个别访谈。问卷调查结束以后，随即对问卷进行阅卷分析。同时，结合问卷答题情况，即刻对学生进行谈话访问。

（三）数据分析

1.定性分析。对问卷进行归纳整理。分析错误理解的结果及类型，并对产生错误理解的原因进行分析。

2.定量分析。 分类整理每一个学生的问卷答案，对其理解层次水平进行界定。得到全体参与问卷调查学生理解水平的分布图。

四、研究结果

（一）正确的理解

1.直观水平。画出直观图，并在图上请学生圈一圈，平均分，得到正确结果。（典型学生作品见图 1）

2.计算水平。列竖式，通过除法运算法则算出正确结果。（典型学生作品见图 2）

3.抽象水平。

（1）正确计算，用画图法验证结果的正确性。（典型学生作品见图 3）

（2）正确计算，用语言来说明结果的正确性。例：324 里包含了 3 个百，2 个十，4 个一，三个百先平均分给 3 个人，每人得 100，2 个十平均分给 3 个人，每人得 6，还多 2 个（一），2 个加 4 个是 6 个，平均分给 3 个人，每人得 2 个，合起来是108 个。

（3）正确计算，用乘法来验证结果的正确性。例：因为12*6=72，所以 72÷6=12 是对的。

（4）正确计算，用减法来验证结果的正确性。例：648—108—108—108—108—108—108=0，减了 6 次就减完了，没有多也没有少。

4.形式水平。正确计算，能够用乘法分配率的延伸了验证结果的正确性。例：324÷3=（300+24）÷3=100+8=108

（二）错误的理解

1. 除法计算仅限于表内试商，超过范围就不知如何计算。（典型学生错误见图 4）

2. 简单的能够画图，在图上分一分，有一个数位不够分的，就无能为力了。（典型学生错误见图 5）

3.只会用机械地法则进行计算，并出现错误，不能发现。（典型学生错误见图 6）

（三）学生理解水平现状

根据以上对于学生理解正确与错误的判断，以及水平层次划分，得出两三位数除以一位数运算学生理解水平现状如下表：

五、结论

（一）对于两三位数除以一位数的运算，学生在学习之前就有比较好的直观认识基础。有接近一半（45.7%）的学生在无明确暗示的情况下，选择了用画图等直观的方法来解决现实生活中出现的问题，其中的大部分都能得到正确的结果。

（二）要达到运算理解的程序水平是比较容易的。在课堂教学前达到该水平的学生就有 34.3%，经过访谈得知他们都是通过长辈教授、培训班学习等提前学习的方式达到了这种理解水平。在课堂教学后，达到该理解水平层次的百分比增长是最迅速的，增长了 25.7 个百分点。达到这一水平层次的学生，无论是课堂教学前还是课堂教学后，往往呈现出知其然（明确算法），而不知其所以然（不能与算理相沟通）的共同特点。

（三）从程序水平到抽象水平的提升，并未如我们想象中的那样顺利，特别体现在是课堂教学后，这一水平层次的增长幅度并不是很大，这与《新课标》中强调的学生对于算理的理解，是不吻合的，急需我们在教学设计上有所改进。

（四）要达到运算理解的形式水平，学生存在很大困难，课堂教学前达到这一水平的学生不到 2%，即使经过课堂教学后，达到这一水平的学生也不到 10%。这与学生所处年段以及知识储备（如乘法与除法的关系了解的局限性）都是息息相关的。

六、教学建议

（一）重视直观

虽然学生很难在形式层次上理解两三位数除以一位数的算理，但却有 45.7%的学生还是能够从直观层次来解决问题。依此，我们应该在教学设计时加强直观教学，辅助数学教学的开展，提升教学质量。

从直观情境引入，让学生充分经历分一分的过程，从可以直接分的数据到不能直接分的数据，借助学生原有的直观理解水平，造成矛盾冲突，为需要借位计算的除法在找到牢固的直观操作经验支撑，突破百位、十位余数的处理难点。

（二）强调估算

同样是根据学生直观理解水平达到的现状，他们中的绝大部分都能在没有提示或者简单提示的情况下，从直观层面感知两三位数除以一位数的商应该是几位数。如，324÷3，3 个百，2 个十，4 个一，分给 3 个人，每人能分到 100 吗？又如：240个学生，6 个老师分坐 6 辆车，每辆车会有 100 个人吗？那每辆车大概有多少人？

这样沟通计算结果与现实情境之间的联系，无论是在计算前确定商的位数，还是计算后进行反思检查，都是是减少学生错误的一个很好方法。

（三）不急简化

在教学后依然有近 40%的学生无法从程序水平提升到抽象水平，这与我们要求学生在初学时就采用最简便的竖式表示形式有很大的关联。

两三位数除以一位数的竖式计算是经历了数千年的发展，抽象和概括出来的。竖式计算中省略的部分，高于学生的生活经验与认知层次，要让他短时间接受比较困难。因而，也就成为了学生理解上的难点，导致对知识的掌握囫囵吞枣，只知其一不知其二。

由此，两三位数除以一位数的教学中，要还原竖式中隐去的数量。我们不能急于教學最简便的竖式表示形式，在教学初期，允许学生保留一些“原始”的竖式呈现形式（图 6），让学生经历逐步优化竖式的过程，从而在感悟中不断沟通算理和算法。

（四）分层设计

基于学生所处的年段以及知识储备，形式理解层次不应该成为教学设计中的人人必须达到的目标。但是，我们可以在两三位数除以一位数的竖式教学中，将竖式试商的每一个步骤与横式的拆分相结合（图 7），呈现在学生面前，让更多地学生能够进入形式理解的层次，实现真正意义上的分层设计，差异发展。

参考文献：

[1]中华人民共和国教育部.全日制义务教育数学课程标准（实验稿）[M].北京：北京师范大学出版社，2011.

[2]陶雪鹤.小学数学数与计算教学的回顾与思考[J].课程·教材·教法，1999，（8）：31–35

[3]巩子坤.有理数运算的理解水平及其教与学的策略研究[D].西南大学，2006.

浙江省杭州市萧山区盈丰小学，浙江 杭州 311200