用好“星号题”提升思考力

2019-09-10金溢李芳邵汉民

人物画报 2019年2期

金溢李芳邵汉民

摘要：笔者在对人教版四年级上册教科书中“带星题”多维分类的基础上，通过“带星题”的难度和学困分析，继而在相对简单的“带星题”上，引导学生在“疑问”中丰富概念、在“说理”中提升推理、在探究中构建模型，对难度较大的“带星题”则采用专题拓展的方式，以实现学生思考能力的提升和学科素养的有效发展。

关键词：带星题;思考力;四年级上册

教材中的练习题是数学教科书的重要组成部分。根据习题的功能可以分为三类：一是紧扣教学内容的基本题，它是教材中例题的模仿及适度变式，以巩固新知识，形成技能为主;二是紧扣教学内容但难度大一点的“星号题”，它是对课本基础知识和基本技能的拓展和延伸;三是难度较大的思考题，这些思考题有些与教材知识点有联系，有些则是内容相对独立的一道难题。三类题中的“带星题”蕴含着许多思想方法，对于学生独立思考能力的培养发挥着不可替代的作用，但是由于课堂时间限制等原因，大家往往会比较忽视，没有深入挖掘它蕴含的价值。于是，从学科核心素养落实的角度分析“星号题”，利用“星号题”培养学生良好的数学素养，形成数学思维方式转变是很值得我们研究的一个内容。带着这样的思考，笔者以人教版教科书“带星题”的整理教学为例，进行分类分析、策略构建等两个方面进行实践研究。

一、多维分类，指向思维特点

人教版教科书四年级上册“带星题”总共有 6 题，我们从学习领域、思维特点、难易程度等三个方面对学生在解决问题过程中遇到的困难进行了分类分析。

（一）依据学习领域分类

四年级上册的“星号题”分布在“数与代数”“图形与几何”两个学习领域，具体所在单元：数与代数中有 2 题，分别在第一段单元“大数的认识”和第四单元“两位数乘三位数”;图形与几何中共 4 题，其中第三单元“角的度量”中有 2 题，第五单元“平行四边形和梯形”中有 2 题。

“星号题”一般都是出现在一个单元的知识点学习完了之后的练习题中，或是在教学完几个相关联的知识点之后的练习中，习题的综合程度比较高，思考性比较强。

（二）依据思维特点分类

四年级的学生思维水平已经开始从直观形象向抽象逻辑过渡，开始学习运用归纳、类化和逻辑推理等思维方式。依据四年级孩子的思维特点，我们从概念理解、推理能力、模型构建这三个方面对四年级上册的 6 道“带星题”进行了思维特点和学习困难的分析。具体分类分析如下。

（三）依据难易程度分类

在对“带星题”以上两个维度分析的基础上，我们对这 6题进行难度的综合分析。

基于对“星号题”的多维分类，以及习题难度分析，并结合当前核心素养取向的育人理念，我们认为可以从课内渗透、专题拓展这两方面结合起来，来更好地发挥带有思维含量的“带星题”，更好地拓展学生的思路，开发创编同类型题目，让更多的孩子从中受益。

二、课内渗透，提升思维品质

简单的、中等难度的“星号题”，往往是对概念、原理、法则以及逻辑关系的理解，据此解释和解决较复杂的常规问题，并对其中的不同变式作出比较。这类题蕴含的思想方法我们在课堂教学的过程中可以逐步进行渗透。

（一）在学生“疑问”中丰富概念

小学阶段，有些概念的呈现不是那么规范、严谨、全面，导致学生在学习这些概念的时候，会产生疑问。学生的“疑问”就是学生的一种需求的表现，有些概念虽然书本没有明确呈现，但是在练习中却是多次出现，那么我们在新授课时就可以进行渗透。

如：大于 180°小于 360°的角是优角？在教学“角的分类”这一课时教材只出现：锐角、钝角、直角、平角、周角的概念，这些角分为两类，一类是固定角，分别是直角、平角和周角，另一类是区间角，分别是锐角<90°，90°<钝角<180°。在学习的过程中学生就会产生这样的疑问：大于 180°小于 360°的角叫什么角呢？并且在教材练习（P16 页第 15 题）中的 “星号题”就是有关优角度数的计算（图 3）。

“疑问”是学生的一种需求更是学生的兴趣。兴趣是最好的老师，浓厚的兴趣可以激发学生的求知欲、探索欲。所以“疑问”的产生是我们教学的契机，在学生的产生疑问的时候，恰当对一些概念的进行补充，可以开阔学生问题解决的思维。

（二）在学生“说理”中提升推理

四年级的学生，他们的思维已经从形象思维逐步向抽象思维提各，他们的表达形式已经从口头表达逐步向书面表达发达。但是，很多的说理题，学生想说说不出来，说的出又写不出来，写出来又不规范。因此，我们引导学生在遇到说理题的时候从会说到会写这样的一个过程顯得尤为重要。

1 一题多解，激励学生说理

启发学生用学过的知识、概念来说理，是培养学生推理能力的最主要手段和基本途径。每个学生思考问题的方式不同，允许不同水平层次的学生运用不同的方式进行表达。

如：计算优角度数时的“一题多解”（图 2）“一题多解”强调学生的积极主动参与，而且强调让学生获得成功的体验，让学生在数学实践过程中学习数学，在现实生活中应用数学，丰富数学知识及数学问题的现实背景。

2 利用直观，引导学生表达

诚然，依据由小学生的思维特点决定，小学数学学习过程中的数学推理，往往需要借助于直观与数学直觉，即在很多情况下，数学结果是“看出来”的。

如图 3，重叠的角，标上∠3。学生就很顺利的进行表达：因为∠1+∠3=90°，∠2+∠3=90°，所以∠1=∠2

语言是思维的外显形式，直观则使得抽象的数学发现与表达得外显，实现数学思维“看得见，摸得着”。这两者的结合，让学生不再觉得对抽象的数学难以表达。在对∠1 和∠2 相等的说理中，笔者充分利用直观，引导学生进行表达，然后通过变式练习，深入挖掘充分理解，提升了学生的推理能力。

（三）在学生“探究”中实现建模

在四年级上册中有三个层次的计数问题，即线段计数、角的计数，四年级下册又有三角形计数。这三类题目其实是属于同一类型，但是学生往往不能顺利的数出有序的排列的图形计数的问题。这三类计数问题有相同的思路，因此在教学中可以迁移策略，形成数学计数的基本策略。

小学生往往对一些新奇的东西往往比较好奇并充满兴趣，因此他们有很强的探究欲望。我们对简单的线段和角的计数问题进行探究激发他们的学习兴趣构建模型，然后再对较复杂的三角形计数问题进行模型运用。

三、专题拓展，提升思考能力

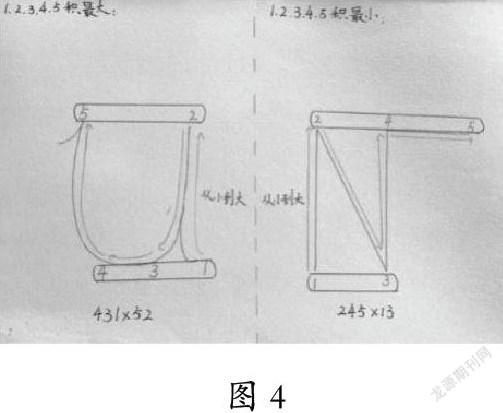
对于较难的“带星题”，它所涉及的知识点多，数学思维训练的价值大，，可以专门作为“一课一题的材料，作为拓展性课程的内容。如教材 P50 第 12 题： “0、1、2、3、4 这几个数字，组成三位数乘两位数求乘积最大最小的问题。”这是一道富有思考性的计算题，使学生经历丰富的推理过程，将对计算中的各种相关知识有更通透的理解，是很有价值的。因此，我们采用以下三种方式进行专题拓展。

（一）构建递进型题组，促进思维深刻性

递进性题组是指把有联系习题按由简到繁、由易到难的顺序进行组合。让学生在依据解决问题的过程中，由前一题的学习经验为基础，探究更复杂的问题。对于第 6 题笔者采用了以下的三个层次的题组。

题组中四个题，由数的最值，到和的最值，再到積的最值，前三个问题的解决，为第四个问题的解决做足了铺垫。

（二）构建对比型题组，提高“思辨”能力

对于最值原理学生已经有了理解，并且会找在有 0 的情况下，最大和最小三位数乘两位数的积之后，安排了下面的练习。

末尾的 0 无论放在两个乘数的哪个末尾，积是一样的。因此，当把 0 改成 1，就会产生于“两位数×两位数”时产生积的大小区别。思考这样的题，有助于增进学生对整数多位数计算的理解。

通过题组进行对比练习，让学生能够发现问题的差异，有利于克服方法选择的盲目性，培养数学思维的灵活性，提高问题解决的能力。

（三）创编运用，提高应用意识和创新意识

最值问题中有很多策略，我们不仅仅是让学生学会做题，更是为了更好的理解背后的数学道理。要求学生把最值问题的解题策略记录下来，并鼓励他们教会同伴。这样的学习方法，锻炼了学生的沟通表达能力（如图 4）。

通过对四上年级“带星题”的实践研究，为我们今天研究其他年级“带星题”的梳理、教学提供了策略。如果将学生的数学素养看作一个坐标系，那么数学知识、技能就好比横轴上的要素，而数学思想方法就是纵轴的内容，数学中的“带星题”则是联接它们的桥梁。

参考文献：

[1]曹培英.跨越断层，走出误区[M].上海教育出版社.2019：151-171