浅谈洛必达法则在高中数学导数教学中的应用

庞廷军

摘 要：函數与导数是数学高考试题中的压轴题，多数是求参数的取值范围问题，分类讨论思想的应用时常贯穿于这类题型，也是大多数学生感觉比较困难的一类题型，分类讨论应怎样讨论从哪儿开始讨论，这是多数学生感觉比较难掌握的地方;分离参数求解就避免了这类问题的出现，但是有时也会遇到新的一些问题，如分离参数以后构造的新的函数有时会遇到分母在极值点没有意义，或者函数值倾向于无穷大，这时学生就无从下手了，应用大学的一些简单的知识如洛必达法则就迎刃而解了。

关键词：洛必达法则;高中数学;导数

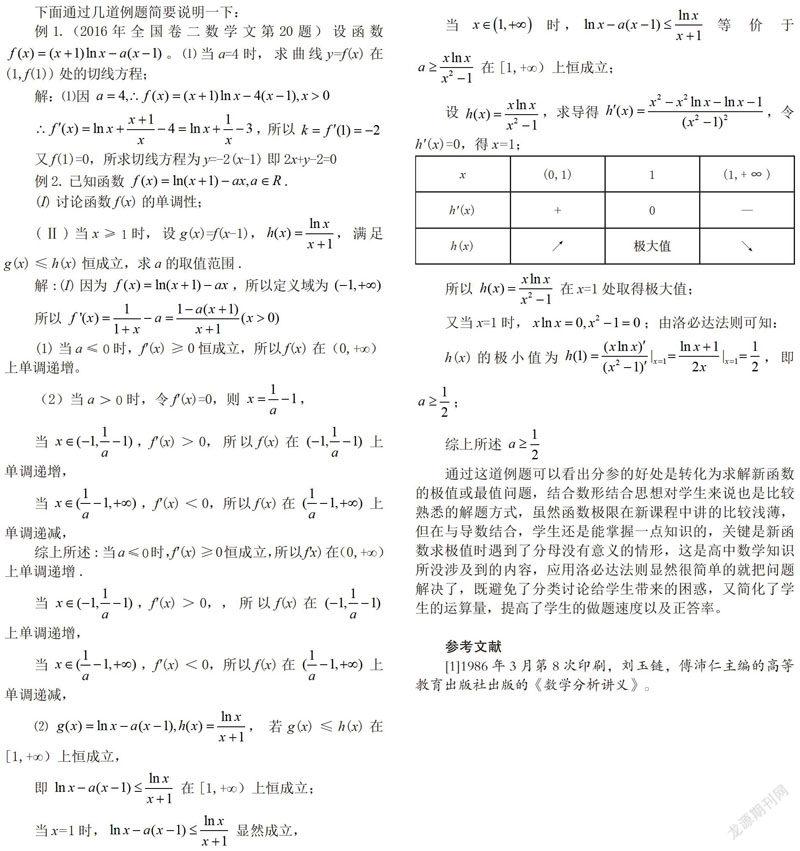
下面通过几道例题简要说明一下：

综上所述

通过这道例题可以看出分参的好处是转化为求解新函数的极值或最值问题，结合数形结合思想对学生来说也是比较熟悉的解题方式，虽然函数极限在新课程中讲的比较浅薄，但在与导数结合，学生还是能掌握一点知识的，关键是新函数求极值时遇到了分母没有意义的情形，这是高中数学知识所没涉及到的内容，应用洛必达法则显然很简单的就把问题解决了，既避免了分类讨论给学生带来的困惑，又简化了学生的运算量，提高了学生的做题速度以及正答率。

参考文献

[1]1986年3月第8次印刷，刘玉链，傅沛仁主编的高等教育出版社出版的《数学分析讲义》。