金属薄板材料冲击性能研究进展

刘牧东

摘要：金属薄板材料已广泛应用于航空、航天、汽车和船舶等工程结构的生产和制造，对于金属薄板材料冲击性能的研究也受到了国内外学者和工程界的高度关注。本文综述了近年来金属薄板材料冲击性能的试验研究，分析了金属薄板材料冲击性能的表征方法，归纳了金属薄板材料冲击性能的有限元仿真技术，明确了研究中尚未解决的问题，需要进一步探索。

关健词：金属，薄板，冲击，试验，表征方法，有限元仿真

中图分类号：V215.9 文献标识码：A

弹性力学中将板厚与面内最小特征尺寸的比值在1/8～1/5范围内的板材定义为薄板，目前工程上金属薄板材料的厚度通常为0.2～4mm[1，2]，已广泛应用于航空、航天、汽车和船舶等行业。金属薄板材料在工程应用中存在大量的冲击行为，如航空器受到飞鸟的冲击、航天器受到碎片的冲击以及船只受到冰山的冲击等，冲击行为发展迅速，破坏过程短暂，难以进行准确预测，对结构的安全性造成威胁。然而，目前人们仍不能完全掌握金属薄板材料冲击行为的物理本质和变化规律，许多学者在这方面进行了分析和研究，为金属薄板材料冲击的试验开展、性能表征和有限元仿真奠定了基础，具有重要的理论意义和应用价值。

1 金属薄板材料冲击性能试验研究

针对金属薄板材料的冲击行为进行了大量试验研究，通过试验了解冲击头、试样、表面处理方法，以及环境温度等因素对金属薄板材料冲击性能的影响。

（1）冲击头质量、形状和尺寸

R.S.J.Corran等[3]采用不同质量的冲击头对金属薄板进行冲击试验，研究冲击头质量与冲击极限速度间的关系，发现冲击极限速度随着冲击头质量的增加而减小，并且减小的幅度先快后慢。

T.Borvik等[4]试验研究了三种不同形状（半球、圆柱和圆锥）冲击头对Weldox 460E钢材薄板冲击结果的影响，发现半球和圆锥形冲击头的冲击极限速度相近，但明显大于圆柱形冲击头的冲击极限速度;圆锥形冲击头产生的变形最大，其次是半球形冲击头，最后是圆柱形冲击头。

穆建春[5]试验研究了不同圆锥半角尺寸的冲击头对金属材料圆形薄板冲击失效模式的影响，试验结果表明，当冲击头的圆锥半角尺寸较小时，冲击头直接穿透金属薄板而形成孔洞，发生刺透型失效;随着冲击头圆锥半角尺寸的增大，冲击区域主要会发生剪切变形，冲击头也不再穿透金属薄板材料，其失效模式转变为剪切型失效。

（2）试样尺寸和夹持方式

N.Jones等[6]以不同长宽比（1～2.5）的低碳钢矩形薄板为研究对象，试验探究长宽比对冲击性能的影响，试验结果表明，当试验的冲击速度为5～13m/s、冲击质量为25～200kg时，矩形试样不同的长宽比对冲击穿透能的影响很小。

D.Bonorchis和G.N.Nurick[7]试验研究了低碳钢薄板边界处的夹持高度对冲击脉冲和冲击凹坑深度的影响，选取的夹持高度分别为0mm、16mm和32mm，冲击头直径40mm，试验结果表明，随着薄板边界处夹持高度的提高，冲击脉冲加强，但冲击凹坑深度变化很小，说明边界处的加持高度会影响冲击脉冲，但对凹坑深度的影响作用不明显。

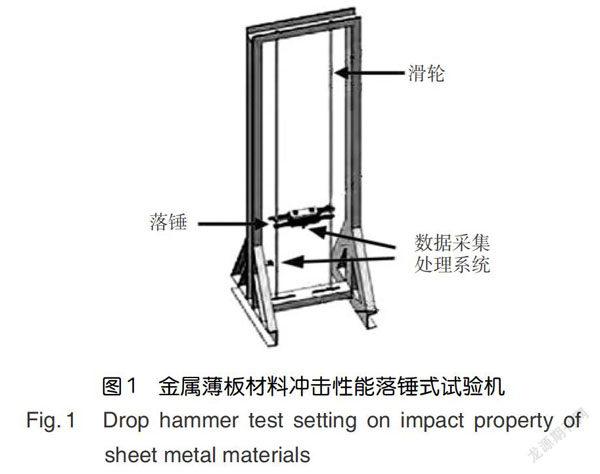
王守财等[8]对铝合金薄板进行低速冲击试验以研究飞机金属蒙皮的冲击性能，采用落锤式试验机开展冲击试验（如图1所示），铝合金薄板试件通过螺钉夹持在试验台上以模拟蒙皮与桁条的连接方式，通过调整落锤的高度获得不同冲击能量对应的冲击性能。

（3）表面处理方法

D.C.Lou等[9]对NVE36钢材薄板进行渗碳和渗氮处理，试验研究渗碳和渗氮表面处理对材料冲击性能的影响，试验结果表明，渗氮处理后试样的冲击极限速度下降6%，而渗碳处理后的冲击极限速度增加了27%～29.4%，这说明渗碳处理使低强度钢材薄板的抵抗冲击能力明显增强，而渗氮处理使材料的抵抗冲击能力减弱。

E.Ozsahin和S.Tolun[10]采用Co-Mo-Cr和ZrO₂兩种涂层对6061-T651铝合金薄板进行喷镀，试验研究等离子表面喷镀方法对材料冲击极限速度和凹坑深度等性能的影响（如图2所示），试验结果显示，两种等离子表面喷镀方法均能提高铝合金薄板的冲击极限速度，并减小了冲击的凹坑深度，使得铝合金薄板材料的抵抗冲击能力显著增强。

J.K.Holmen等[11]试验研究了4种回火方式（退火、自然冷却、极限强度冷却和过度冷却）对6070铝合金薄板材料冲击性能的影响，试验结果表明，经过退火后试样的冲击极限速度最小、产生的冲击碎片最少，经过极限强度冷却后试样的冲击极限速度最大、产生的冲击碎片最多，而经过自然冷却和过度冷却过程后试样的冲击性能介于前两者之间，这说明通过控制回火过程的方式，能够提高铝合金材料的屈服强度，进而增强抵抗冲击的能力。

（4）环境温度

J.A.Rodriguez-Martinez4[12，13]分别在288K常温和213K低温下对TRIP 1000钢材薄板和2024-T3铝合金薄板进行冲击试验，试样尺寸为80mm方板，冲击头为圆锥形，冲击速度不超过4.5m/s，试验结果表明，当环境温度由288K常温降至213K低温时，两种金属薄板材料的冲击能吸收能力提高，薄板的塑形弯曲变形增强，说明低温习境对金属薄板材料的冲击性能产生有益影响。

李卫军等[14]分别在4种环境温度（20℃、0℃、-20℃和-40℃）下对40CrNiMoA钢材薄板进行冲击试验，试验结果表明，在20℃，0℃和-20℃温度下，钢材薄板发生韧性冲击失效;当环境温度由-20℃降至-40℃时，材料的冲击失效模式逐渐由韧性向脆性转变，40CrNiMoA钢的韧脆转变温度约为-20℃。

可见，冲击头的质量、形状和尺寸，试样的尺寸和夹持方式，表面处理方法以及环境温度等均会影响金属薄板材料的冲击性能，其影响因素多、作用复杂。但目前对于金属薄板材料冲击作用机理的研究较少，可以进一步在试验的基础上，采用扫描（SEM）和透射电镜（TEM）技术分析断口微观结构，探寻冲击引起的晶体变形、位错滑移、凹坑演变和断裂失效等机理的变化。2金属薄板材料冲击性能表征方法研究

金属薄板材料的冲击性能通常借助能量和动力学两种方法进行表征。

（1）能量法

N.Perrone和P.Bhadra[15]采用指数型应变率强化模型表征低碳钢和钦合金材料的本构关系，并采用经验抛物线模型表征位移场和速度场，计算了低碳钢和钦合金薄板材料的冲击塑性功，能够获得在冲击载荷下材料塑性变形的理论解析表达式。

R.Zaera等[16]针对圆形金属薄板冲击载荷问题，考虑其外力功率等于动能变化率与塑性功率之和，建立了金属薄板的中心位移解析式，分析结果表明，薄板所受的径向弯曲内力、周向弯曲内力以及转动惯量均对计算结果产生影响，其中，径向弯曲内力的影响最大，周向弯曲内力的影响小于径向弯曲内力，而转动惯性的影响几乎可以忽略。

L.B.Chen R J.L.Yang["1采用线性和指数应变率强化模型表征圆形金属薄板中心冲击的本构关系，根据冲击塑形能等于冲击动能的能量守恒原理，构建了金属薄板中心冲击最大横向位移的解析模型。

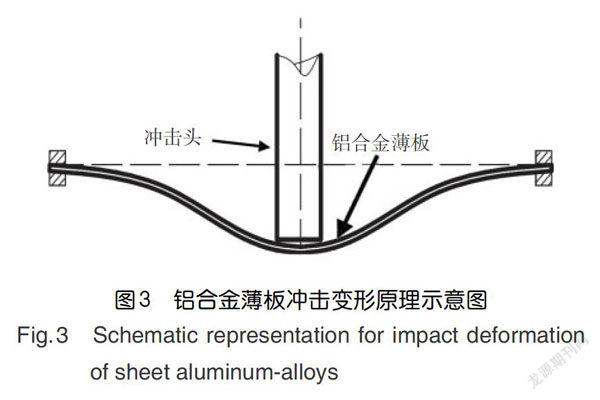
D.Mohotti等[is]针对铝合金薄板材料的低速冲击问题（冲击速度为3-15m/s）进行研究，图3显示出了冲击变形的产生原理，采用Johnson-Cook应变强化模型表征铝合金材料的本构关系，并根据薄板冲击塑形功等于冲击头动能损失的守恒原理，建立了铝合金薄板材料冲击的挠度解析模型，模型的有效性在试验中得到了验证。

王守财等181在试验的基础上，采用Johnson-Cook模型表征本构关系，并根据能量守恒原理建立了凹坑深度与冲击能之间的关系，发现低速冲击载荷下的薄板凹坑损伤与冲击能量之间近似呈線性关系，模型的训算结果与试验吻合良好。

（2）动力学法

M.J.Forrestal等[l9]建立了铝合金薄板材料高速冲击（冲击速度为0.3-lkm/s）的接触动力学模型，并求解微分方程，获得其冲击速度与冲击凹坑深度之间的关系，模型的计算结果与试验数据吻合良好。

Q.S.Wei[207针对低碳钢薄板锥形物冲击问题，考虑了弯矩和薄板内力的影响，借助动力学方法构建薄板内部和边缘处的塑性变形微分方程，获得了凹坑变形与冲击能量之间的关系，但模型中存在隐式计算，求解过程复杂，对其广泛应用造成不便。

N.Jones[2'7针对金属材料矩形薄板冲击问题，采用动力学平衡方程建立塑性变形与冲击能量之间的关系，获得了关于薄板边界条件的函数表达式，分析结果说明，在冲击头质量与薄板面积之比很大的条件下，边界条件对于金属薄板材料塑性变形的影响可以忽略，模型的有效性还需要在简支边界条件下进一步验证。

N.Jones 1211采用线性速度场表征金属薄板材料的塑性铰链，根据动力学平衡方程建立了在质量冲击、脉冲压力和爆炸载荷条件下金属薄板材料的横向位移解析模型，获得了圆形和矩形薄板的函数表达式，并与试验结果进行对比，发现冲击载荷、金属材料的动特性参数和薄板约束方式均会对其冲击性能产生影响，需要获得更加丰富的试验数据，进一步完善和发展金属薄板材料冲击性能的理论模型。

从上述文献中可以看到，目前主要考虑了内力、本构关系、速度场和位移场等因素的影响，建立金属薄板材料冲击性能表征模型，其中，内力方面主要考虑了面内弯矩、薄膜内力、切应力和转动惯量等因素;本构关系方面常根据不同的材料选取对应的塑性强化模型，铝合金材料选取应变强化模型，而低碳钢和钦合金材料则选取应变率强化模型;而速度场和位移场则是根据试验数据选取对应的抛物线型、指数型或三角函数型经验模型进行表征。这些因素确定后，借助能量和动力学方法获得金属薄板材料冲击性能表征模型的解析解，其中，能量法基于准静态假设进行分析，需要材料的冲击时间远大于应力波的传播时间;而动力学法的求解过程较为复杂，需要进一步简化和完善。3金属薄板材料冲击性能有限元仿真技术研究

通过有限元仿真模拟金属薄板材料的冲击行为，研究了网格的划分以及本构关系和失效准则的选取对冲击性能仿真结果的影响。

（1）网格划分

金属薄板冲击的有限元仿真主要借助拉格朗日型网格进行模拟，但由于材料在冲击时会发生较大变形，引起网格畸变而导致计算失真，在采用拉格朗日型网格的同时常伴随自适应型网格进行划分。G.T.Camacho和M.Ortiz[2'7采用自适应型网格分析金属薄板材料的冲击问题，以网格形状的内切圆和外接圆半径之比作为网格划分的依据，并根据不增加网格阶次的方法对其进行重新划分，能够减少网格畸变对金属薄板材料冲击性能仿真结果的不良影响。

T.Borvik等[247通过有限元模拟了Weldox 460E钢材薄板在三种不同形状（半球、圆柱和圆锥）冲击头作用下的冲击过程（如图4所示），采用自适应和拉格朗日型两种方法进行网格划分，研究不同的网格划分方法对冲击性能模拟结果的影响，分析发现，对于半球和圆柱形冲击头的情况，自适应和阿格朗日型网格计算的剩余速度结果相近，其相对差异不超过7%;但对于圆锥形冲击头的情况，自适应型网格预测的冲击极限速度精度更高，且其能量损失减少了10%，这是由于自适应型网格解决了冲击时的网格畸变失真问题，从而提高了仿真模拟的有效性。

此外，冲击过程中常存在较大的变形，为此可采用无网格方法模拟金属薄板材料的冲击性能。由于不依赖于网格的特性，无网格方法在解决大变形引起的网格扭曲问题上具有十分显著的优势，但该方法的计算稳定性较差且效率较低，需要进一步研究和探索。

（2）本构关系和失效准则选取

T.Borvik等[25]选取了Johnson-Cook本构关系分析Weldox 460E钢材薄板的冲击性能，仿真模拟穿透过程中产生的碎片和薄板的失效形式，分析发现，本构关系中的温度、应变率和应力水平等参数对钢材薄板的冲击性能仿真结果有较大影响。

S.Dey等[26]分别选取了Johnson-Cook和Zerilli-Armstrong本构关系模型，借助LS-DYNA非线性有限元方法模拟Weldox 460E钢材薄板的冲击极限速度，分析结果显示，在高温和高应变率条件下，Johnson-Cook本构关系模型的仿真效果要优于Zerilli-Armstrong模型，因此，Johnson-Cook模型预测的冲击极限速度精度更高。

A.Rusinek等[27]直鹧∪ower Law、Johnson-Cook和Rusinek-Klepaczko三种本构关系模型模拟不同冲击速度下的金属薄板冲击性能，仿真结果说明，对于较大范围的冲击速度（40～300m/s）情况，Power Law和Johnson-Cook本构关系模型无法同时模拟高、低两种冲击速度性能，需要根据材料的应变率进行分段表征;而Rusinek-Klepaczko模型则可以对较大范围的冲击速度情况进行模拟，但模型形式复杂、参数多，计算结果的稳定胜较差。

陈小翠等[28]选取与应变、应变率和温度相关的塑性本构关系模型描述剪切带，并在能量方程中考虑剪切带形成中的热传导效应，编写了适用于金属薄板材料高速冲击的新单元进行有限元分析，仿真结果表明，基于新单元的有限元计算收敛稳定、精度较高，且由于考虑了热传导效应，网格的敏感胜小。

K.Teng和T.Wierzbicki[29]分别选取了最大切应力准则、Cockcroft-Latham准则和Bao-Wierzbicki准则模拟圆形钢材薄板高速冲击（冲击速度为156.6～307.2mm/s）的失效形式，对比分析发现，最大切应力准则受到冲击温度的影响，其切应力先增后减，与薄板冲击性能单调递增的形式不一致，因此，最大切應力准则不适用于模拟金属薄板材料冲击的失效形式;Cockcroft-Latham准则中定义的冲击特性参数难以确定，为仿真计算带来不便，这一准则预测的冲击剩余速度精度较低，不适用于模拟金属薄板的高速冲击性能;Bao-Wierzbicki准则考虑了塑性应变破坏的影响，能够较好地模拟圆形钢材薄板的冲击剩余速度，仿真得到的冲击失效形式也与试验相吻合，具有很好的适用性。

大量文献表明，有限元仿真力祛已广泛应用于金属薄板材料冲击性能的模拟，仿真过程中网格的划分、本构关系和失效准则的选取等因素均会影响计算结果的有效性。但是，目前还未能完全解决冲击大变形引起的网格扭曲问题，可以加强对无网格方法的研究，同时，也尚未找到一种形式简单、训算稳定准确的本构关系进行仿真模拟，这都需要进一步修正和完善。

4 结束语

金属薄板材料冲击性能的研究主要包括试验、表征方法和有限元仿真技术三个方面，取得了显著的研究成果，帮助人们认识了金属薄板材料冲击特性和变化趋势，为评估材料冲击性能、优化设计和检修维护提供了依据，减少由于冲击而引发事故所造成的损失。然而，金属薄板材料的冲击行为复杂、影响因素多，尚未完全认清，未来可以进一步在以下几方面开展研究：

（1）在试验的基础上，可以进一步研究金属薄板材料冲击的作用机理，采用扫描和透射电镜技术分析断口微观结构，探寻冲击引起的晶体变形、位错滑移、凹坑演变和断裂失效等机理的变化，为工程故障分析及维护提供帮助。

（2）冲击性能表征方法中，能量法基于准静态假设进行分析，应用范围受限。而动力学法的求解过程较为复杂，可以进一步简化。

（3）有限元仿真中可以加强对无网格方法的研究，为冲击大变形引起的网格扭曲提供解决途径。还要进一步开发出稳定而准确的计算方法，以便更有效地模拟金属薄板材料的冲击行为。

通过理论与工程实践相结合的方法，相信未来对金属薄板材料冲击性能将会有更为深刻的认识和理解。

参考文献

[1]杨桂通.弹性力学[M].北京：高等教育出版社，2005.

[2]GB/T15825.1-2008金属薄板成形性能与试验方法[S].中国标准出版社，2008.

[3]Con-an R S J，Shadbolt P J，Ruiz C.l山pact loading of plates：An experimental investigation[J].International Journal ofImpact Engineering，1983，1（1）：3-22.

[4]Borvik T，Hopperstad O S，Berstad T，et al.Perforation of12mm thick steel plates by 20mm diameter projectiles withflat，hemispherical and conical noses：Part Ⅰ：experimental study[J].International Journal of]mpact Engineering，2002，27（1）：19-35.

[5]穆建春.金属薄板在圆锥头弹体正冲击下的破裂模式[J].爆炸与冲击，2005，25（1）：74-79.

[6]Jones N，Birch R S，Duan R.Low velocity perforation of mildsteel rectangular plates with projectiles having different shapedimpact faces[J].Journal of Pressure Vessel Technology，2008，130（3）：1047-1057.

[7]Bonorchis D，Nurick G N.The influence of boundaryconditions on the loading of rectangular plates subjected tolocalised blast loading-importance in numerical simulations[J].International Journal of Impact Engineering，2009，36（1）：40-52.