Wiener指数，Hyper-Wiener指数，Harary指数与图的哈密顿性

李星星，余桂东，任丽芳

（安庆师范大学数学与计算科学学院，安徽安庆246133）

连通图G的Wiener指数W(G)[1]，是指G中任意两个顶点的距离之和，即,若记，则有图G的hyper-Wiener[2-3]指数作为Winner指数的推广，记为WW(G)，

图G的Harary指数[4-5]是化学图论中另一个非常有用的拓扑指数，,记，则有。

下面先介绍两个相关引理。

引理1[6]设G为n阶连通图，，如果，则G是哈密顿-连通的，除非。

引理2[6]设G为n阶连通图，如果，则G是从任一点出发都是可迹的，除非。

下面给出本文的主要结论及证明。

若G∈NP1，由Winner指数的定义可直接计算得，与定理条件矛盾。

综上所述，假设不成立，即G是哈密顿-连通的。

当G ∈NP1时，由hyper-Winner指数的定义可直接计算出与定理条件矛盾。

综上所述，假设不成立，即G是哈密顿-连通的。

证明 假设G不是从任意一点出发都是可迹的，通过引理2，知或。

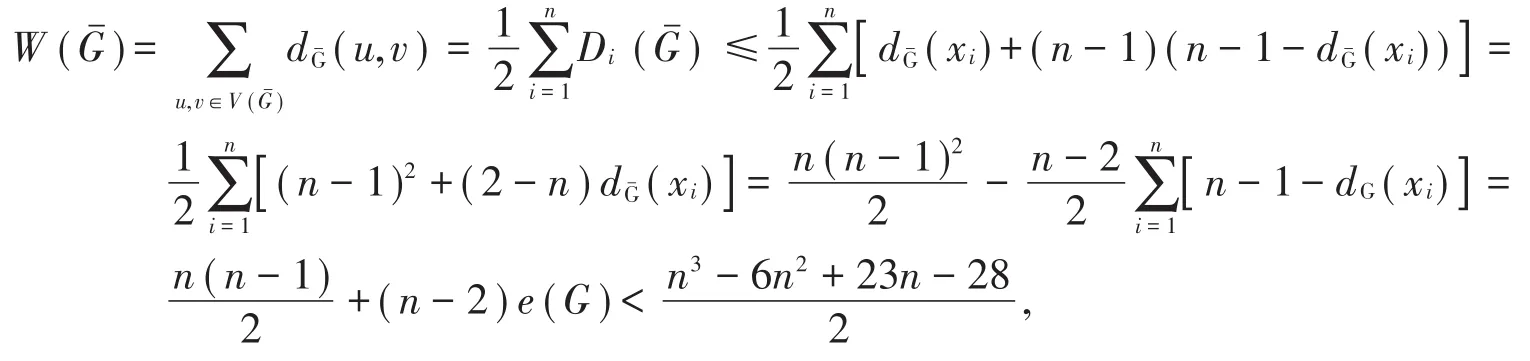
当G∈NP2时，由Winner指数的定义计算可得与定理条件矛盾。

证明 假设G不是从任意一点出发都是可迹的，通过引理2，知或

当G ∈ NP2时，通过hyper-Winner指数的定义计算可得与定理条件矛盾。

综上所述，假设不成立，即G是从任意一点出发都是可迹的。

证明 假设G不是从任意一点出发都是可迹的，通过引理2，知或

与定理条件矛盾。

当G∈NP2时，由Haraary指数的定义计算可得，当n≥8时，

得到G∈NC。当G∈NC时，则由引理2知，G不是从任意一点出发都是可迹的。