一类半线性椭圆型方程边值问题的可解性研究

田梦甜，钟金标

（安庆师范大学数学与计算科学学院，安徽安庆246133）

文献[1]考察了下列半线性椭圆型方程边值问题

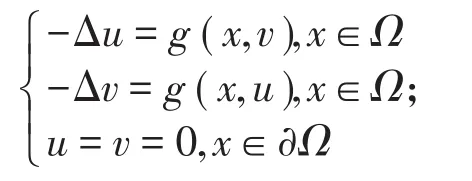
设（1）式中的非线性函数F(x,u)满足下列条件（或部分条件）：关于在上非负局部Holder连续，即，其中M为一个正常数关于s在单调递减；关于s在上单调递减。

1 解的存在性研究

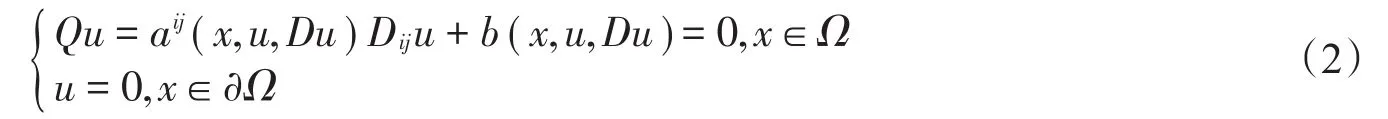
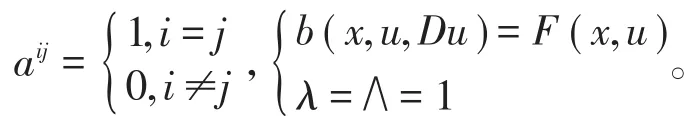
引理1[1]设在Ω中，假设Ω有界，则。

引理2[1]设Q在有界区域Ω中是椭圆的，并假定存在非负常数μ1和μ2，使得：则如果在Ω中满足，就有，其中又如果在Ω中，则有

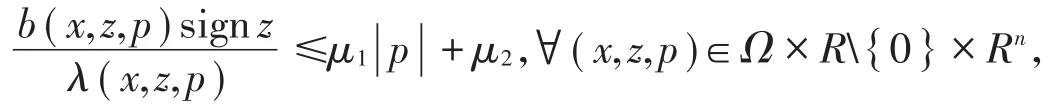
引理3[1]设T是Banach空间B到自身中的紧映射，又设存在一个常数M，使得，对所有满足的x成立，则T有一个不动点。

定义算子T如下，设u=Tv是半线性椭圆型方程Dirichlet问题：

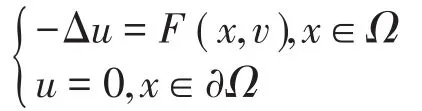
定理1 若条件(A2)成立，则问题（1）的解只能是正解。

证明 由条件(A2)及问题（1）方程可得：

例1 考察问题

解的存在性，其中Ω为Rn中有界光滑区域。因满足条件由定理2知，问题（4）存在有界正解。

2 解的唯一性定理

定理3 若条件(A4)成立，则问题（1）至多只有一个正解。

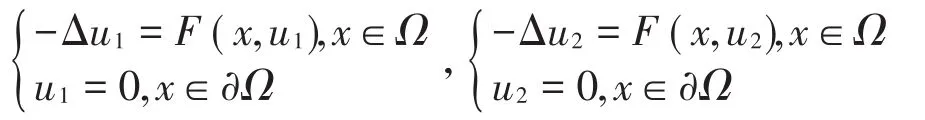
证明 设u1、u2为问题（1）的任意两个正解，则有成立，两个方程相减得：两边乘以u1-u2后在Ω上积分，并利用Green第一公式得，由 条 件知 ，从而得即结合知即问题（1）至多只有一个正解。

定理4 若条件(A5)成立，则问题（1）至多存在一个有界正解。

证明 设u1,u2为问题（1）的任意两个正解，则有成立，从而，因此，，两边乘上，并在Ω上积分，同时由可得：再由条件可得：u1≡u2，从而问题（1）至多只有一个解。

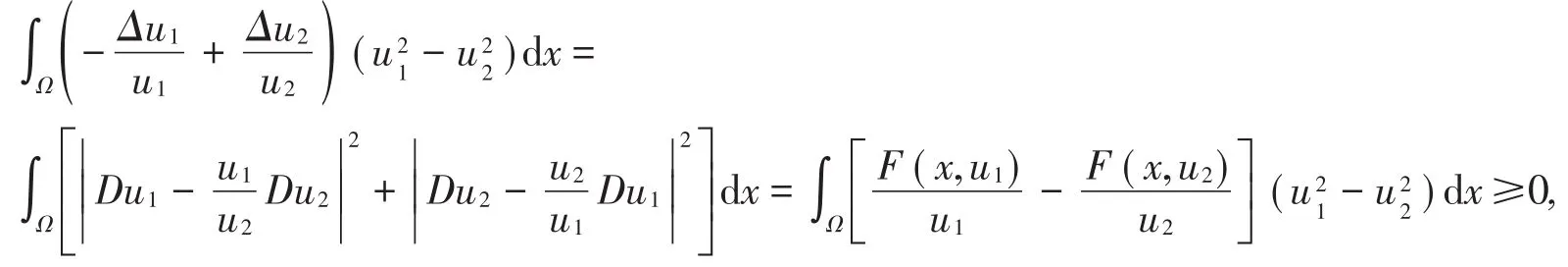
3 总结

本文通过考察半线性椭圆型方程边值问题的解，研究解的存在性并且给出解的唯一性定理，同时给出了证明。文中（A1）到（A5）是函数F(x,u)所分别满足的5个条件，这5个条件在不同定理中使用会得出不同的结论，从而得出文章的4个重要定理。