一类Schrödinger-Virasoro型李代数的Verma模

张 鑫

（合肥科技职业学院基础部，安徽合肥230000）

本文用N,Z,C分别表示正整数集、整数环和复数域；文中所指向量空间的底域都是复数域C。Schrödinger-Virasoro代数是一类重要的无限维李代数，其结构理论和表示理论得到很多专家学者的关注[1-3]。在文献[4]中，Roger等在研究Schrödinger-Virasoro代数的同调理论和表示理论时引入了一类Schrödinger-Virasoro型李代数，它是由复数域上的一组基生成的，并满足下面非平凡的李括号运算：此后，文献[5-7]分别研究了它的李双代数结构、量子化和李共形代数等结构理论，文献[8-9]分别研究了一类Schrödinger-Virasoro型李代数的Harish-Chandra模和秩为1的自由模。

令加法群Γ=由复数C和复数加法运算组成，其单位元为0；封闭性：∀a,b∈C,a+b∈C；结合律：∀a,b,c∈ C,(a+b)+c=a+(b+c)；逆元：∀a ∈ C,a-1=-a。现给出Schrödinger-Virasoro型李代数定义。

定义1 一类Schrödinger-Virasoro型李代数gsv是由复数域上的一组基生成，并且满足下面的非平凡的关系式：

下面介绍Verma模的定义，为计算Verma模的不可约性作准备。在Γ上定义一个与其加法相容的全序“”，即“”可得“”。当且时，记。令，有且 gsv有一个三角分解这里这时 gsv 的泛包络代数为当且时，元素和 1 成了的一组基。令是C上由va,b,c生成的一个1-维向量空间，即把看作满足的一个模，这时通过令把Va,b,c变成模。

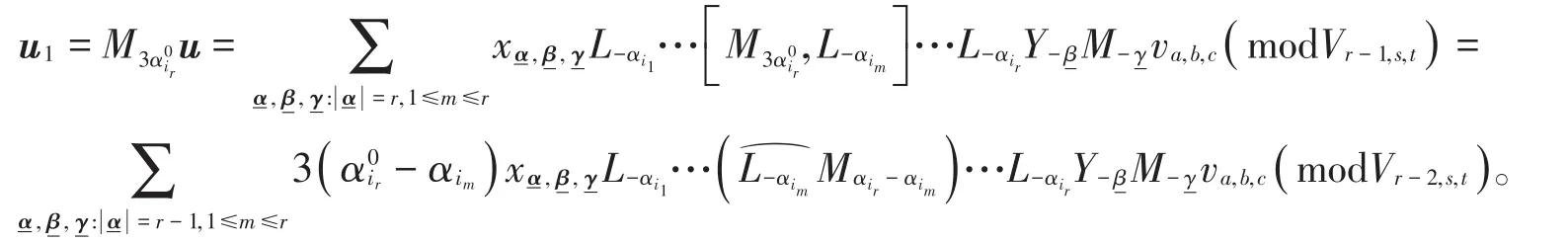
重复上面过程，当0≠a0∈C时，则

重复上面过程，当0≠a2∈ C时可得。因此，得到综上所述，是不可约的。