基于GA随机共振的模糊SVDD轴承性能退化评估*

2019-09-09高淑娟

组合机床与自动化加工技术 2019年8期

高淑娟

(淄博职业学院机电工程学院，山东淄博 255013)

0 引言

轴承作为旋转机械中的关键部件，一直是状态监测和故障诊断领域的热点研究对象。而滚动轴承是工业中应用最为广泛的一种通用机械部件，据统计在机械设备的各种故障中，滚动轴承故障占有相当大的比例，因此，研究滚动轴承性能退化评估的技术和方法，对轴承的故障诊断以及剩余寿命预测有重大的理论意义和工程应用价值[1-2]。

随机共振由于在提取微弱故障信号方面具有较好的效果而得到了广泛的应用，其主要原理是通过噪声来加强故障信号中的微弱成分[3]。张超等针对随机共振无法处理大参数信号的问题，提出了一种变尺度自适应随机共振方法[4]。张仲海以系统输出信噪比为指标，通过粒子群算法动态调整系统参数与压缩比系数，从而实现最优随机共振的效果[5]。然而上述方法在利用龙格-库塔求解时可能会发散，为解决这一问题，本文利用稳定约束条件下遗传算法优化的自适应随机共振来提取微弱故障信号，保证该方法的收敛性。

支持向量数据描述是一种在统计学习理论和支持向量机基础上发展起来的分类方法。这种方法具有针对目标样本点和非目标样本点进行分类，有效处理小样本数据等优点，因此得到了广泛的关注[6-7]。然而，SVDD也具有几个突出的缺点，一是对异常点太过敏感；二是训练过程中，所有样本对超球体构建的贡献率相同，这是不合理的[8]。为解决上述问题，本文结合模糊理论中的隶属度因子来实现对样本点的区分。为提高轴承性能退化评估的效果，本文提出一种通过改进随机共振信号提取与模糊SVDD相结合的方法来实现轴承的性能退化定量评估。

1 稳定约束GA随机共振

在微弱信号处理方面，随机共振理论在近几年得到极大的发展，其基本原理是周期信号和一定量的输入噪声在非线性系统的作用下，会在某一“共振”点大幅度提高系统输出的信噪比，从而使得原来被强噪声淹没的周期信号凸显出来。而变尺度随机共振的提出为随机共振在大信号检测领域的应用开辟了新的途径，并已得到了广泛的应用[9]。但应用该方法对实测信号进行处理时，由于信号幅值和频率未知，根据特征频率确定频率压缩比R并不现实。而且在实际条件下，噪声的强度也是未知的，这就给变尺度随机共振的应用带来了困难。本文利用带稳定约束的基于遗传算法的随机共振方法来进行信号提取。

经典遗传算法由于其在优化方面的鲁棒性、快速性较好得到了广泛应用，首先将系统参数b和频率压缩比R定义为优化参数，令系统参数a=1。系统参数a、b的大小与粒子跃迁的势垒高度ΔU的大小具有较大的关系。当a值固定，通过调整b值的大小，可以在变尺度随机共振基础上，得到适应新系统的最优参数取值。

然而在应用提出的遗传算法随机共振方法进行数据处理时发现，在一些情况下应用龙格-库塔方法求解，得到的结果会出现发散现象，导致寻优计算溢出,使随机共振输出不稳定，根据文献[10]可知要取得稳定的随机共振效果，应保证R和b变化范围满足:

(1)

同时可以看出，当xi取值过小时，b值的取值上限会很大，这样不仅增大了搜索范围，影响寻优速度，而且b值过大对提高稳定性并没有太大帮助。文献[11]以信噪比增益为测度，分析了a=1时，b取值对信噪比增益的影响，给出了b值取值范围为[1,100]，即b<1或b>100时，信噪比增益已经小于1，所以本文同样取b值范围为[1,100]。

基于稳定约束GA优化的随机共振信号提取算法步骤为：

STEP1：给定b值搜索范围为[1,100]，为了保证系统的稳定性，初始R值搜索范围定义为：

(2)

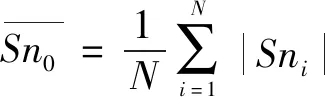
(3)

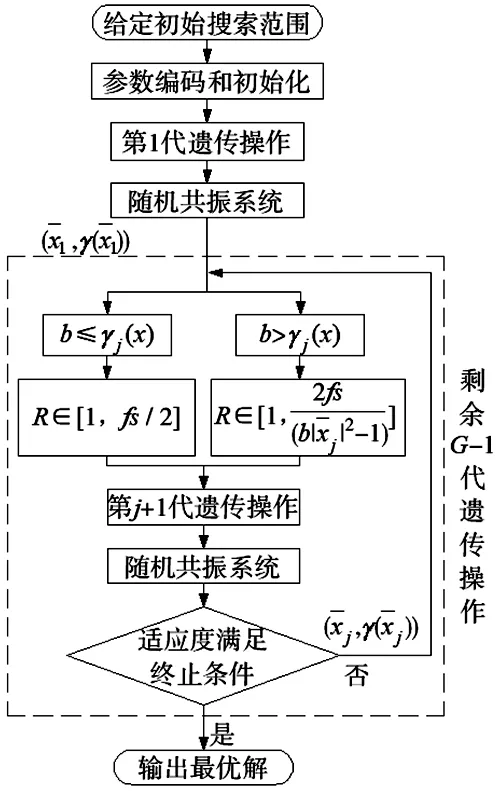
图1 改进的随机共振算法流程

2 模糊支持向量数据描述

2.1 支持向量数据描述

图2 利用超球体来包围目标样本

2.2 模糊支持向量数据描述

为了描述数据样本的重要程度或所属类别的不确定性，即模糊性，为数据样本xi引入模糊隶属度系数si(0≤si≤1)。si越大，说明xi越重要，在非类中所占的权重就越大；si也可以反映样本xi属于非目标样本的隶属程度，si越大，说明xi属于非目标样本的程度越大。利用模糊系数si，可以将标准的SVDD扩展为模糊SVDD[13]。

因此，高维特征空间中的内积运算可以定义为：

(4)

模糊支持向量数据描述最终目的是为了让所有权重特征向量(si+1)φ(xi)都能够包含在体积最小的一个超球体之内。模糊支持向量数据描述的超球体必须满足：

(5)

约束条件为：

(6)

由Lagrange定理得：

(7)

分别对R、ξi及c求偏导：

(8)

(9)

(10)

与支持向量数据描述的推导过程类似，对式(7)进行简化可得：

(11)

此时，对于一个新样本z,通过非线性模糊映射得到的超球体中心距离计算公式为：

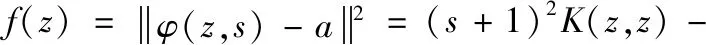
(12)

若f(z)>R2,则判断为非目标样本，否则即为目标样本。

3 GA随机共振与模糊SVDD的性能退化评估

3.1 退化评估流程

基于随机共振与模糊支持向量数据描述的轴承性能评估方法具体步骤如下:

(1)首先利用稳定约束自适应随机共振对获得的振动信号进行预处理，提取相应的时域与频域特征信号。设经过随机共振预处理后的振动信号为x(n)，共有n个数据点，提取14个常用的时域统计特征与12个频域特征信号。

(2)计算轴承的模糊支持向量数据描述的模糊隶属度系数；振动信号样本xi的绝对能量E(xi)愈大，则轴承偏离正常运行状态愈远，根据经验可选用升岭形分布函数作为隶属函数，a1为良好状态的轴承总能量，a2为轴承振动能量报警上限[14]。如模糊隶属度系数计算公式如下：

(13)

其中，A=[E(xi)-0.5(a1+a2)]/(a2-a1)，绝对能量的计算公式为：

(14)

(3)选取多个能形象描述轴承性能衰退状况的特征向量作为模糊支持向量数据描述方法的输入量；

(4)构造最优超球体，即构造二次规划问题的目标函数；

(5)计算所选取的特征向量的融合指标，最后得到性能退化评估指标监测系数IN；通常每一个指标包含的信息太少，并且只对特定阶段特定缺陷有效，对轴承当前运行状态的反映不够全面。然而一个好的性能评估方法应能够充分利用多重特征信息，因此，本文采用模糊支持向量数据描述的方法构造出能很好描述轴承状态的指标。

通过将新获取的测量数据输入到正常数据训练过的模糊支持向量数据描述，计算其监测系数IN，该系数就可以作为一种新的量化衰退评估指标。因此，定义监测系数IN表达式为：

(15)

式中，f(z)为样本离超球体球心的距离，R表示超球体半径。

3.2 自适应失效阈值的计算

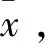
(16)

其中，ts表示可以确定的轴承处于正常状态的时刻，T(t)表示t时刻的检测系数IN，mean和std分别代表均值和标准偏差。阈值Th的求解分为3个阶段；第1阶段数据来源于早期无故障状态，是一个固定值；第2阶段将t时刻的T(t)与t-1时刻的进行比较，若T(t)在Th(t-1)范围内，则将T(t)纳入原始数据，计算Th(t)；第3阶段为其后连续Nu个IN值均超限，则定义t=te为轴承性能退化的初始时刻。

4 试验与结果分析

4.1 轴承疲劳试验简介

本实验采用的轴承疲劳试验机如图3所示，该试验机主要由转动部分、加载部分和测量部分组成。振动的采样频率为25600Hz，温度的采样频率为10Hz，转速为1500r/min，径向加载力为5000N。轴承疲劳试验机工作到轴承故障时停止。另外为了避免整个实验台发生故障(同时出于安全考虑)，在振动的加速度超过了20g时测试停止。

图3 轴承疲劳试验机

4.2 结果分析

首先采用基于稳定约束条件的遗传算法优化自适应随机共振对实验测量得到的信号进行处理，其中遗传算法的进化代数为100，种群数目为50，交叉概率为0.6，变异概率为0.1。最后经过遗传算法优化得到相应的适应度函数的收敛曲线如图4所示，从图中可知，该方法在迭代次数达到22次时收敛于-4.75dB,此时相应的共振参数b=26.2561，频率压缩比R=10.2445。原始信号信噪比与经过GA稳定约束的随机共振后得到相应的轴承振动信号如图5和图6所示。

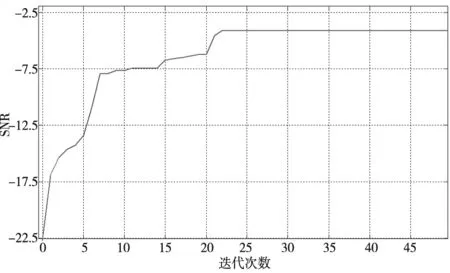
图4 SNR优化收敛曲线

图5 原始信号信噪比

图6 GA随机共振输出信噪比图

由图5和图6对比可得原始数据的信噪比在-22dB附近上下波动，然而经过稳定约束自适应随机共振处理过的轴承微弱故障信号的输出信噪比保持在-4.8dB左右，结果表明，经过GA稳定约束随机共振处理后的轴承振动信号能够提高轴承的微弱故障信号的信噪比，且能够保证提取方法的收敛性，提高了该算法的使用范围。

对预处理过后的振动信号进行特征信号提取，获得相应的时频域特征信号。在特征向量选择上，根据文献[16]可知时域信号与频域信号能够反映轴承退化的过程。时域特征中，和轴承衰退程度线性相关，随着损伤加深，幅值指数增加，所以但对早期损伤敏感度不够，易受工况影响。其特征向量如图7所示。而在频域特征中也是和轴承衰退程度成线性相关，随着实验时间增加，损伤增加，幅值指数增加，能形象描述轴承性能衰退状况。如图8所示。

(17)

图7 方根幅值特征信号变化图

(18)

图8 频域信号pf6变化图

轴承性能衰退评估目的就是构造一个指标，能够真实反映轴承运行状态的变化规律。因此本研究选取方根幅值、pf6两个特征信号前11000s部分共同作为模糊SVDD的训练样本，得到相应的超球体，然后利用该超球体模型求得样本距离球心的距离，进一步计算可以得到相应的自适应失效阈值Th与监测系数IN，然后为了使得评估结果更为精确，对数据进行平滑处理，最后实现轴承退化性能的定量评估。

表1 轴承退化评估结果对比

图9为利用本文的改进随机共振与模糊支持向量数据描述结合的轴承性能退化评估结果图，图10为利用本文的改进随机共振预处理与支持向量数据描述进行性能退化评估的结果图，图11为未经过随机共振预处理，单纯利用原始特征信号作为模糊支持向量数据描述的输入进行性能退化评估的结果图，表1为三种退化评估的相关数据对比。

从图9和表1中可以看出在开始运行的一段时间内，监测系数IN始终在一段较小的范围内变化，说明此时轴承处于正常状态，在一段时间的运行之后，检测系数IN超过阈值，根据图中的交点得到轴承开始失效的时刻为8920s，随着继续运行，发现轴承的监测系数急剧增大，整个退化变化过程中拐点较为明显，能够较为形象地表现出了轴承的失效情况。

图9 GA随机共振与模糊SVDD退化评估图

图10和表1结果显示改进随机共振预处理与支持向量数据描述评估方法检测系数超过阈值的时刻为10190s，比模糊SVDD的评估方法晚了1270s，说明模糊SVDD较SVDD能够较早的发现轴承的失效点，这主要是因为模糊隶属度的加入区分了样本对超球体模型的贡献值，使得超球体模型更接近实际。而在后期，SVDD波动的幅值更大，反应轴承状态的效果较差。而且可以看出SVDD相较于模糊SVDD来说，由于未区分各个样本点的贡献值，所以相应的样本离球心的距离均小于模糊SVDD。