改进梯度下降法的机载云台姿态解算*

王 铎，袁 亮，侯爱萍，姜 宏

(新疆大学 机械工程学院，乌鲁木齐 830047)

0 引言

随着国内外无人机(Unmanned Aerial Vehicle, 简称UAV)研究领域的迅猛发展，人们对无人机扩展功能的需求愈发强烈。无人机视觉技术作为其中较为突出的分支，在测绘、监控和安防等方面具有广阔的应用前景，而高度自稳定的机载云台则是无人机视觉技术获取稳定图像数据的基础。微机电系统(Micro-Electro-Mechanical System, 简称MEMS) 作为云台主要传感器，承担着实时反馈云台姿态，维持机载相机稳定的重任。

通常使用的MEMS中，陀螺仪存在严重的偏移积分累计误差[1]，需多传感器的融合处理，同时考虑机载云台载重量和有限的计算性能，选择合适的姿态解算尤为重要。扩展卡尔曼滤波(Extended Kalman Filter, 简称EKF)虽然具有较高的精准度[2-3]，但较大计算量和复杂性一直是EKF的难题。R Mahony等[4-5]提出的显式互补滤波算法(Explicit Complementary Filter,简称ECF)在较少的计算量下拥有较高的性能[6]，但面对复杂环境需要调整参数，适应性较差。S O H Madgwick等[7-8]提出的基于梯度下降法的姿态解算已在微控制器中应用[9]，其核心思想是通过梯度下降法缩小加速度计与地磁计表征的姿态四元数误差[10]，并与由陀螺仪计算得到的姿态四元数线性融合得到最优的姿态。该算法即能保证较高精度的同时又能满足云台计算量小的要求，无需调整参数适应性较强，但在较大运动加速度或姿态变化剧烈时，加速度计较差的动态性能对整体算法影响较大，解算出的姿态信息仍有所欠缺。

本文作者将卡尔曼滤波与梯度下降法相结合，提出一种改进梯度下降法的云台姿态解算。利用卡尔曼滤波器对加速度计进行预处理，减小剧烈振动引起的加速度噪声对姿态解算的影响，再通过梯度下降法消除姿态四元数误差，从而得到矫正后较为精准的姿态信息，并与同样是较低计算量的显式互补滤波作对比，印证了改进算法的优劣性和可行性。

1 姿态参考系

1.1 四元数及姿态解算

(1)

(2)

根据z-y-x的旋转顺序，可由四元数求解出最终姿态角：

(3)

1.2 角速度表征的姿态更新

由四元数描述E系相对S系的变化率，则有陀螺仪在t时刻表征的姿态四元数微分方程与更新方程：

(4)

(5)

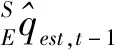
2 梯度下降法

虽然陀螺仪的动态稳定性良好，但易累计误差产生漂移，而加速度计的静态稳定性好，动态性能较差，二者融合后yaw角误差较大，地磁计能够有效缩小yaw角误差，因此需要多传感器融合。

由梯度下降法通用迭代公式应用在本文中有：

(6)

(7)

(8)

(9)

将梯度(9)代入迭代公式(6)，得到t时刻的加速度计和地磁计表征的姿态四元数更新方程：

(10)

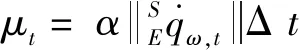
为融合多传感器表征的姿态四元数，由文献[9]可得融合的梯度下降法姿态解算四元数更新方程：

(11)

3 改进梯度下降法的加速度计预处理

为保证系统最终输出可靠、稳定的姿态角，本文在进行基于梯度下降法的姿态解算前，先对加速度计输出的数据进行卡尔曼滤波预处理。

在常规卡尔曼滤波[11]中，考虑如下线性离散系统有状态方程[12]：

xk+1=Axk+ωk

(17)

zk=Cxk+νk

(18)

系统下一点状态预测：

(19)

状态预测方差：

Pk|k-1=APk-1AT+Qk-1

(20)

卡尔曼增益计算：

Kk=Pk|k-1CT[CPk|k-1CT+Rk]-1

(23)

系统状态更新：

(21)

协方差更新：

Pk=[I-KkC]Pk|k-1

(22)

此处^为预测值，利用上述卡尔曼滤波器来减小加速度计动态误差对梯度下降法的影响，提高云台姿态反馈的真实性和稳定性。本文提出的改进梯度下降法叙述完毕，算法原理如图1所示。

图1 改进梯度下降法的云台伺服系统

4 实验结果与分析

4.1 实验平台

本文实验平台是以ARM-CortexM3为内核的STM32F103微处理器搭建的三轴无刷云台。惯性测量单元(Inertial measurement unit，简称 IMU)选用MPU6000，该测量单元为集三轴陀螺仪与三轴加速度计的MEMS传感器，采样频率25Hz，地磁计选用HMC5883L电子指南针罗盘。

实验参考的真实姿态由无人机飞行控制器pixhack px4提供，pixhack拥有双IMU、双地磁计和GPS等多种传感器来获得稳定、真实的姿态角。实验平台实物如图2所示。

图2 机载云台姿态解算系统实物

4.2 静态实验

为验证改进算法的综合性能，本文作者进行了两组对比实验：第一组为静态实验，以测试算法在平台空转情况下的静态性能；第二组为动态实验，以测试算法在复杂飞行环境中的动态性能。

静态实验中，在无人机电机未安装螺旋桨空转情况下，测试改进梯度下降法的静态性能，并与真实姿态和显式互补滤波姿态解算作对比，静态实验局部放大结果如图3所示。

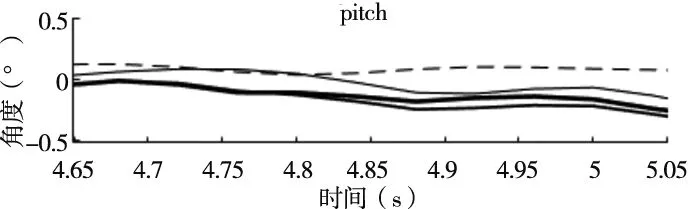
图3 静态实验下各姿态算法

表1给出了各算法姿态角与真实姿态角的均方根误差，由此可知改进算法整体精确度高于梯度下降法算法，整体姿态角精确度提高15.25%，但相较于显式互补滤波姿态解算，梯度下降法姿态解算及其改进算法静态性能明显较差，其根本原因在于梯度下降法的动态步长在平稳环境下步长过大，无法快速得到最优解，在静态环境中性能较差。

表1 静态实验姿态角均方根误差

4.3 动态实验

在动态实验中，无人机分别完成起飞-偏航前进-定点悬停-爬升-返航降落的动作，实验天气环境：雨后风力3级，以此复杂环境来测试改进梯度下降法的动态性能。动态实验姿态角对比结果由图4所示，局部放大图如图5所示。

图4 动态实验姿态角对比

表2给出了各算法解算出的姿态角与真是姿态的均方根误差，由表中可知，改进梯度下降法在动态性能上要明显优于显式互补滤波姿态算法，改进算法在梯度下降法的基础上，有效减小了加速度计的动态误差影响，精确度提升了27.53%，已基本接近由飞行控制器解算的真实姿态。图6为动态实验机载相机航拍图像。

表2 动态实验姿态角均方根误差

图5 动态实验局部放大图

图6 动态实验相机航拍图像

5 结论

本文针对低成本的机载云台系统，提出了一种改进梯度下降法的姿态解算，利用卡尔曼滤波对加速度计数据预处理，减小加速度计动态误差对姿态信息的影响，同时与显式互补滤波作比对，印证了改进梯度下降法姿态解算在静态与动态性能中的优劣势。在静态性能实验中，显式互补滤波要明显优于改进梯度下降法，证明了合适的动态步长对于梯度下降法的必要性。在动态性能实验中，改进梯度下降法精度要优于显式互补滤波，证明了其算法在机载云台系统中的可行性。