基于压电陶瓷驱动的六自由度空间光学拼接系统*

孙立宁，陈方鑫，董 为

(哈尔滨工业大学 机器人技术与系统国家重点实验室· 哈尔滨·150000)

0 引 言

随着空间科学技术的飞速发展，大口径空间光学望远镜在深空探测和对地观测中发挥着重要作用。由于制作工艺的限制，直径为米级的镜面通常需要数个子镜拼接而成，而不是通过整体加工方式。每个子镜都需要在毫米级范围内实现高精度定位，以便光学系统获得高质量的图像。

与地面环境不同，在设计空间定位平台时，应考虑空间的热效应和真空环境。为了减小温控系统的压力，定位系统所用的驱动模块应尽可能减少其对温度的要求。此外，考虑到真空环境下的冷焊效应，应避免机械传动过程中的摩擦。众所周知，火箭在发射过程中的振动是不可避免的，这将增大装配件的装配误差。但在空间环境中，无法在工况下对机构进行标定。总而言之，空间定位平台的设计应考虑空间适应性(高低温、真空、摩擦)和控制策略的特殊性(简单的运动学，即运动对结构参数偏差不敏感)。

在空间应用中，Stewart平台因其结构简单、刚度高、技术成熟等独特优势，常被用作六自由度定位平台[1-4]。VISTA[5]是一个直径为4m的空间测量望远镜，它利用Stewart机构在5个轴线上对230kg的子镜进行位置调节,实现了1μm和0.1rad的精度。LSST中的镜面是由基于音圈电机驱动的六足并联机构调整的，它能在3060kg负载下实现20μm的定位精度[6]。VST[7]望远镜的主动光学系统也安装了六足并联机构，以调整望远镜管和光学列阵的不正确的相对位置。根据实验研究，该机构可实现1μm的分辨率。

虽然Stewart平台可以用于镜面拼接，但对于某些特定的应用场景，定位平台的方案设计需要综合考虑结构尺寸、系统质量、空间适应性、系统精度、运动学复杂性等因素。因此，作为六足并联机构的一种替代方案，混合机构引起了研究者的关注。混合机构一般由多个并联机构串联而成，其运动学比纯并联机构简单。Gaunt[8]设计了一个六自由度的定位平台来校正Altair镜面的位置，Altair是位于夏威夷的Gemini North望远镜。该定位平台是一种将两种三自由度并联机构串联在一起的混合机构，任何期望的单一运动都可以由对应的执行单元实现。Wang[9]提出了一种用于光纤拼接的六自由度定位平台，该平台是由一个三自由度并联机构和一个三自由度串联机构组成，其优点包括结构紧凑、运动学简单、连杆误差零积累等。Cai[10]将一个三自由度平面定位机构与三自由度空间定位机构进行了串联，构造出了六自由度的混合机构。文中提出的解耦控制方法很轻松地解决了运动耦合问题。

与传统铰链相比，柔性铰链具有无返程间隙、无磨损、无摩擦、重复性好的优点，适用于精密工程[11-13]。同样的原因，它也适用于空间环境。通常情况下，PZT的行程只有自身材料的0.1%。因此，在实现具体应用时，需要配合行程放大机构来使用[14-15]。Kim[16]研制了一种基于压电材料的三自由度空间定位平台。该平台由一个新的紧凑桥式放大器驱动，运动平台的运动范围和分辨率分别为190μm和4μm。Chao[17]提出了一种六自由度混联柔顺机构，该机构结合了两个由杠杆放大机构驱动的并联机构。实验表明，机构的最大行程为130μm，分辨率为50nm。Xu[18]设计并分析了一款XY并联机构。该机构采用两个压电执行机构来实现位移输出。在桥式放大机构的帮助下，其输出行程大约为120μm。

在前人工作的基础上，本文设计了一种用于空间光学对准的、由PZT驱动的六轴高精度定位系统。该系统由三个串联连接的子平台组成，其中每个子平台由位移放大器驱动。

1 机械系统设计

图1为六自由度调整机构的三维实体模型，该机构由三级串联的子平台组成。其中，第一级为空间三自由度机构，第二级为完全解耦的XY并联机构，第三级为冗余驱动的单自由度机构。

(a)机构总览

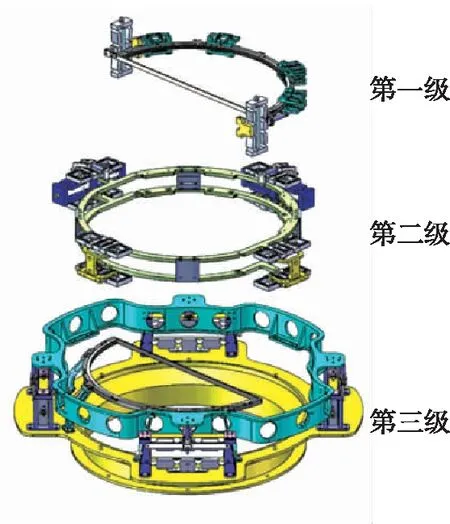
(b)平台爆炸图

(c)机构主要尺寸图1 三维实体模型Fig.1 3D solid model

1.1 空间三自由度并联机构

空间三自由度平台的设计是为了实现X轴、Y轴旋转和Z轴平移。众所周知，位移放大器在放大PZT位移的同时也会减小输出力。因此，不同于以往包含3个驱动模块的设计[19]，这里增加了一个冗余驱动模块，以提高平台的负载能力。考虑到对称性，4个驱动模块呈90(°)排列，如图2所示。

(a)

(b)图2 (a)传统的三支链空间并联机构； (b)四支链空间并联机构Fig.2 (a)Traditional spatial parallel mechanism with three branches；(b)Space parallel mechanism with four branches

平台的每个执行模块均由一个主动线性驱动、被动线性关节、被动虎克铰关节和位移传感器组成。为了减少驱动模块的惯量，主动线性驱动被固定在底座上。被动线性关节起引导作用，可抑制非运动方向的负载力，如图3所示。此外，为了避免光学遮挡，平台的包络线必须被限定在图1所示的圆环内。因此，虽然各种直线电机和音圈电机能够提供超高线性位移分辨率及毫米级的运动范围，但是基于PZT和放大器机构的驱动模块仍因为体积小、结构灵活而成为了该类平台驱动器的优选方案。

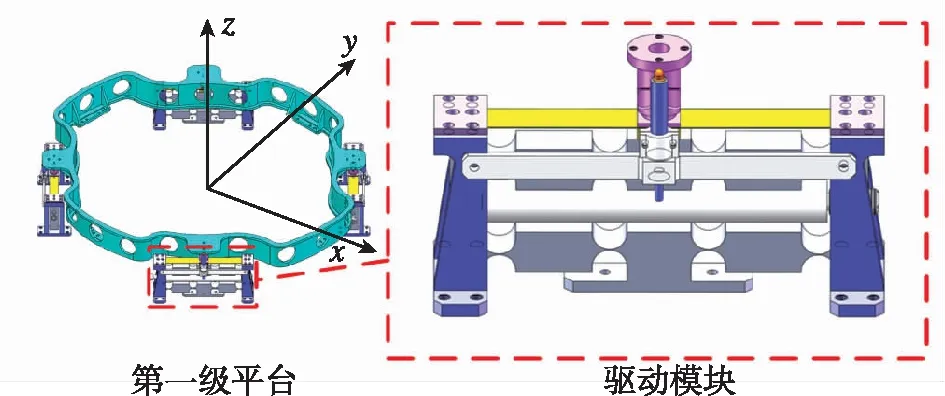
图3 空间3-DOF并联机构及其驱动器Fig.3 Space 3-DOF parallel mechanism and its driver

1.2 XY并联机构

第二级平台负责X轴和Y轴的线性运动。一般情况下，XY二维平台有串联和并联两种设计。串联模式结构简单，但其承载能力低，难以支撑下一级平台和镜面。因此，这里采用并联模式。

具体而言，XY并联平台有2个垂直排列的驱动模块，其中每个模块包含1个线性驱动关节、1个复合平行四边形关节和1个位移传感器，如图4所示。复合平行四边形关节也叫解耦器，其可被看作是2个垂直布置的导向装置。因此，2个相互垂直的直线运动可以实现完全解耦。

(a)第二级平台 (b)驱动模块 (c)原理图图4 第二级平台驱动单元Fig.4 The second platform driver unit

为了减小驱动模块运动方向的尺寸，设计了一款紧凑型放大器[20]。与传统的桥式放大器相比，紧凑型放大器由2个双面桥式机构组成。陶瓷置于双面机构之间，尽可能减小运动方向尺寸。此外，2个解耦器也如此对称布置，以进一步减小运动方向尺寸，如图5(c)所示。

(a)

(b)

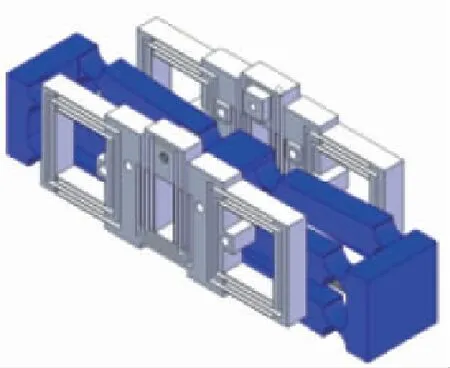
(c)图5 传统设计和紧凑型设计的比较Fig.5 Traditional design versus compact design

1.3 第三级机构

Z轴旋转由第三级平台实现。第三级平台由回转导向装置、驱动模块、位移传感器组成。回转导向装置类似于传统的平行四边形机构，其不同之处在于其延长线将相交于一个旋转点，而平行四边形机构永不相交，如图6所示。放大器的输出端装有片状柔性铰链，以避免径向方向的寄生运动。

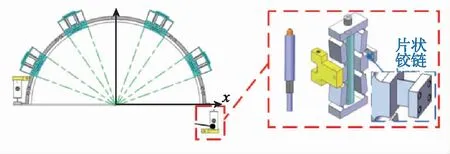
(a)第三级平台 (b)驱动单元

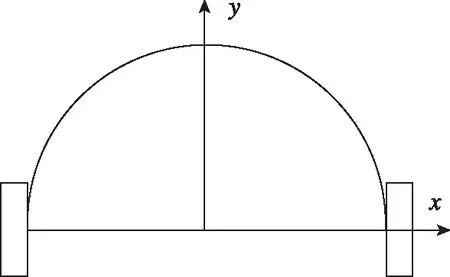
(c)平台的结构简图图6 第三级平台结构图Fig.6 The level 3 platform structure diagram

2 柔性单元的建模

2.1 桥式放大机构

本节将采用柔度矩阵法对桥式放大器进行理论建模。根据弹性梁理论，从坐标系Oi到另一个坐标系Oj的力与位移的关系可以表示为

ei=[Tij]T[Rij]TC[Rij][Tij]Fi

(1)

其中，

[Rij]和[Tij]是转换矩阵，C是铰链的柔度矩阵。

由于对称性的原因，可以只分析该机构的一半。简化模型可以看作是一个一端固定、一端受导向约束的串联链，如图7所示。根据小变形假设，点在链上的位移等于各个力分别作用于链上所产生的位移之和。此外，当施加一个力时，位移等于相关柔性铰链变形的总和。因此，输出点和输入点的位移可表示为

(2)

(3)

F和ε表示力和位移，其下标表示所关注的点。

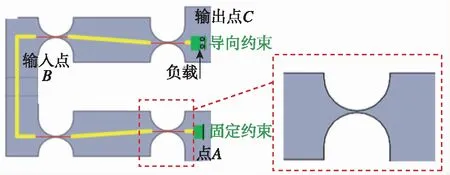
图7 对称模型的约束和尺寸Fig.7 Constraints and dimensions of symmetric models

根据定义，放大倍数和输入刚度可用下式进行计算

(4)

(5)

其中，da和kin表示放大器的放大倍数和刚度。

考虑压电陶瓷的刚度，PZT在放大器中的实际位移为

(6)

其中，lPZT和LPZT分别为PZT的实际位移和名义位移，kPZT为PZT的刚度。根据公式(6)，可得到放大器的实际输出位移

(7)

此外，还需要分析应力，以预测实际输出的最大位移。利用铰链的旋转变形，根据文献[21]，可计算出圆形柔性铰链应力集中部分的弯曲应力

(8)

β=tbridge/lbridge是文献[21]定义的一个量纲为1的参数。此外，最大拉应力可表示为

(9)

旋转变形θ和轴向力Faxial可通过公式(8)和公式(9)获得。为保证放大器的安全运行，弯曲载荷和轴向载荷的最大应力应小于材料的许用应力，即

(10)

其中，na是安全系数。

2.2 柔性导向器

本文将第一级平台的被动线性关节、第二级平台的复合平行四边形机构和第三级平台的旋转导向装置称为导向柔性元件。由于这3个柔性元件的基本柔性单元的变形原理相似，如图8所示，因此可将其放在一起进行讨论。

图8 导向机构Fig.8 The steering mechanism

在以前的文章中，很容易找到柔性平行四边形的建模方法[22-24]。本文提出了一种基于悬臂梁受力公式的平行四边形机构设计方法。一端固定一端受导向约束的柔性梁，可被看作是一个自由端受切向力F和力矩M作用的悬臂梁。由于梁与其几何中心是呈中心对称的，当梁被对称中心分离时，梁的对称中心只被施加一个等效力F′，且该力大小等于F，如图8所示。由悬臂梁的受力公式，可以计算出其末端位移为

(11)

式(11)中，E为材料的杨氏模量，I=bt3/i2为截面绕中性轴的惯性矩。考虑到对称性，导向机构梁单元的位移为

(12)

第一级平台的导向装置可以看作是两个并联的导向单元，其刚度是单个导向单元的2倍。

(13)

图8所示的导向机构由4个串联的导向单元组成，其刚度可计算如下

(14)

复合平行四边形可分为3个平行四边形机构，其中一个垂直排列，另两个水平排列。因此，复合平行四边形机构水平方向的刚度以及第三级平台导向装置的刚度等于平行四边形机构的刚度，而复合平行四边形沿垂直方向的刚度是平行四边形机构刚度的2倍，即有

(15)

根据材料力学和图8中的参数定义，悬臂梁的应力可表示为

(16)

行程与机构刚度的关系可表示为

(17)

结合公式(16)、公式(17)和公式(13)～(15)，3种导向机构的行程可计算为

(18)

2.3 柔性虎克铰

柔性虎克铰精度高、无机械摩擦、无静态阻力、运动平稳无需润滑、易维护、分辨率高和可一体化加工等优点使其在精密机械和微机械中得到了广泛应用。从本质上讲，柔性虎克铰是2个垂直布置的簧片式柔性铰链，如图9所示。其力位关系可由式(1)获得。

图9 虎克铰Fig.9 The hooke joint

3 参数设计及FEA仿真

根据光学系统的要求，3个线性运动的行程和分辨率要求为1mm和1μm；对于旋转运动，行程和分辨率分别为600(′)和1(′)。结合图1(c)所示的几何参数，很容易得到3个平台驱动模块的性能要求。具体而言，第一级平台需要1.6mm行程和1μm精度；第二级平台需要1mm行程和1μm精度；第三级平台所需的行程和分辨率分别为0.85mm和2.1μm。

3.1 放大机构负载特性分析

桥式机构是一种经典的柔性位移放大器。前人在研究中，采用了多种方法对桥式机构进行了分析。然而，以往的研究往往忽略了施加在放大器上的外部负载。对于执行机构而言，在实际工作中不可避免地要承受外部载荷，因此对带有外部载荷的桥式机构进行分析是非常必要的。

在柔性机构中，执行机构一般需要承受两种载荷，即弹性荷载和恒定荷载。弹性载荷主要来自于构件的变形，这在柔性机构中是不可避免的。恒定载荷则来自于平台的重力。分析参数如表1所示，输入位移与放大倍数的关系如图10所示。一般情况下，当选择参数时，放大倍数被认为是一个常数。然而，图10显示放大倍数会受到弹性载荷的影响。从图10(a)可以看出，随着弹性荷载的增大，放大倍数会减小(曲线的斜率会减小)；而当施加恒定载荷时，曲线斜率不变、截距改变，即放大器的初始位置不同。因此，在放大器的设计过程中，必须考虑实际的负载情况。

表1 放大器参数

对上述线形进行理论解释。根据小变形假设，当放大器输入端固定时，输出端的力-位移呈线性关系即为线性弹簧。假设其弹性系数为k0，不加负载时的放大倍数为da0，当施加恒定载荷时，输出位移可表示为

δout=da0δin-k0fload

(19)

对于弹性荷载，其表达式为

δout=δinda0-k0(kloadδin)

=(da0-k0kload)δin

(20)

式(19)为线性方程，其截距由荷载决定。式(20)为比例函数，其斜率受荷载弹性系数kload的影响。这2个方程与图10的结论完全一致。

当考虑两种荷载时，放大倍数可表示为

=da0-k0kelastic

(21)

式(21)表示实际放大倍数由放大器的结构和弹性荷载共同决定。此外，在设计放大器时，应通过式(21)计算其实际放大倍数。

(a)弹性负载

(b)恒力负载图10 输入位移与放大倍数的关系Fig.10 The relationship between input displacement and amplification

3.2 设计参数

由于存在放大极限的现象，柔性桥式放大器的放大倍数很难超过30。考虑到驱动器的负载和制造工艺，实际的最大放大倍数约为20。因此，第一级和第一级平台的压电陶瓷行程为160μm，第三级平台的压电陶瓷行程为120μm。放大器材料采用铝7075-T6，其杨氏模量为71GPa，最大屈服强度为500MPa。结合上述公式，可以预测放大器的实际行程为

(22)

虽然设计参数的选择是一个耗时的过程，但是第3节中建立的模型加速了这一过程。经过多次迭代，放大器和所有导向机构的设计参数如表2所示。

表2 弹性单元的参数

3.3 有限元仿真

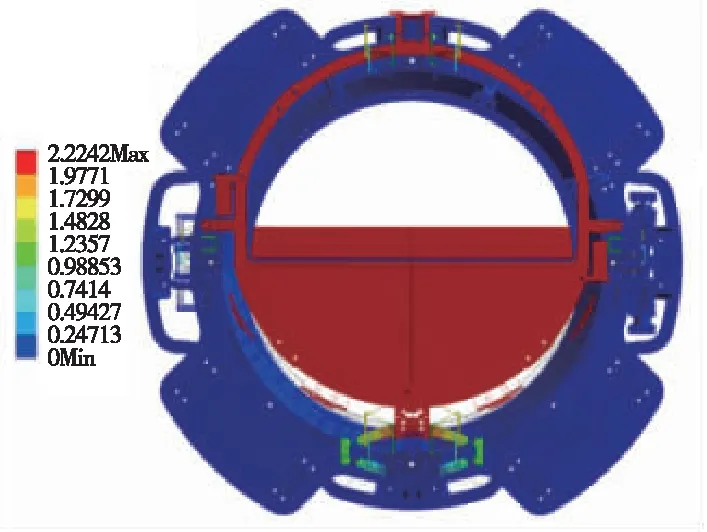
本节通过有限元软件进行仿真分析。需要注意的是，由于在实验过程中，镜子是垂直放置的，因此在仿真环境中需打开沿Y轴的引力场。图11为仿真环境下各自由度的运动情况。假设有限元分析结果足够准确，以机构行程和应力的数值解为标准，评价设计参数的可行性。FEA的计算结果如表3所示。

(a) X轴位移

(b) Y轴位移

(c) Z轴位移

(d) 绕X转动

(e) 绕Y转动

(f) 绕Z转动图11 六维运动仿真Fig.11 Six-dimensional motion simulation

自由度有限元仿真数值分析行程应力/MPa放大倍数解耦率/%放大倍数误差/%θx1336(″)16918.026.24θy1339(″)17018.005.02Z3.06mm16419.120.6719.618.18.22.5X2.22mm17913.930.52Y2.24mm18213.910.5014.534.14.2θz1064(″)15210.75—11.032.5

有限元结果和数值计算结果之间的最大偏差约为8%，出现在对θx和θy的计算中。误差主要是由于忽略了虎克铰的柔度而造成的。此外，数学模型中使用的柔性铰链柔度矩阵也会引入误差。可以看出，第3节建立的模型对设计参数的预测是足够准确的。每个自由度的设计行程都覆盖到了所要求的范围，确保了足够的余量。运动过程中的最大应力远小于材料的屈服应力。值得注意的是，XY轴的旋转耦合分别为6.24%和5.02%，约为其他自由度运动的10倍。在仿真中，左边2个放大器的输入位移为0.16mm，右边2个放大器的输入位移为0(即输入端的相对位置受限)。根据理论，这种情况下放大器的输出理应为0，但在实际过程中检测到的放大器输出端位移为0.179mm，如图12所示。出现这种情况是由于虽然放大器的输入端是固定的，但是当输出端产生反作用力时，驱动单元中的柔性铰链仍会发生变形。在施加外力的情况下，弹性元件不可避免地会发生弹性变形。考虑到这一点，有必要在驱动模块的输出端放置位移传感器，通过闭环控制消除变形现象。

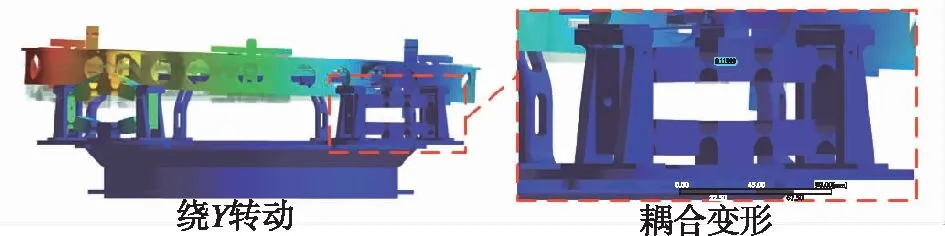
图12 输入耦合Fig.12 The input coupling

3.4 动力学性能

在这一节中，采用有限元法对系统的动态性能进行分析。图13为定位平台的前6阶振动模态，其中第一阶固有频率为19.45Hz。光学系统只需要完成点对点运动，即定位系统是在准静态条件下工作的。因此，该频率满足使用要求。

(a) 一阶模态

(b) 二阶模态

(c) 三阶模态

(d) 四阶模态

(e) 五阶模态

(f) 六阶模态图13 定位机构的模态分析Fig.13 The modal analysis of positioning mechanism

4 实验研究

为了进一步验证设计的可行性，制作并组装了如图14所示的定位系统样机。样机中所有的柔性元件均采用7075-T6铝合金材料制造。与其他合金材料相比，铝合金材料具有较低的密度和杨氏模量。柔性元件采用线切割-电火花加工工艺制造。考虑到上节中分析的输入耦合现象，将线性位移传感器(DONG-DO，测量范围和分辨率分别为2mm和2μm)安装在驱动模块末端，实现闭环控制。下位机与功率放大器、数据采集卡、信号发生器和PID控制器相结合，对各执行模块进行闭环控制。上位机在Labview环境下实现编写，用于各平台的运动学计算。图14(d)为软件操作界面，每个自由度的运动均可被单独控制，平台位置可实时显示。

当第一级被控制时，控制量由逆运动学可得

(23)

对于第二级平台，由于两个自由度的运动完全解耦，因此平台运动直接等于相关的驱动模块输出量

(24)

第三级平台只控制一个自由度的运动

(25)

可以看出，与其他六自由度定位平台相比，该系统的运动学非常简单，这也是该系统的主要优点，如图15所示。

图14 (a)实验平台；(b)工业相机图；(c)电容位移传感器控制界面；(d)上位机软件Fig.14 (a)The experiment platform；(b)the industrial camera diagram；(c)Capacitive displacement sensor control interface；(d)Host software

图15 定位机构控制策略Fig.15 The positioning mechanism control strategy

4.1 工作空间测试

定位平台的工作空间是由CCD相机(DAHENG成像像素大小5.6μm×5.6μm)测量的。在相机的视场内粘贴一个刻度作为标准距离参照，这样便不需要再对相机进行标定了。假设粘贴在移动平台上的刻度是准确的，则可以通过移动前后的两张照片上的同一标记点来评估平台的位移，如图14(b)所示。具体而言，在平台移动前，拍一张照片。在平台沿着运动方向移动到极限位置后，再拍一张照片。将两张照片上标记点的距离与照片上的刻度进行比较，计算出平台的实际位移。在旋转运动方面，利用两台CCD相机对直径两端的位移进行测试，然后用三角函数将线性位移转化为角位移。

为了研究“输入耦合”对运动的影响，实验采用了两种控制模式。第一种模式采用了集成在PZT中的应变片测量PZT的输出位移，PZT在此模式下输出期望位移(局部闭环)。第二种模式在驱动模块的末端放置了一个位移传感器，驱动模块能够在此模式下输出期望位移(全局闭环)。与第一种模式相比，第二种模式可以消除“输入耦合”现象。为了定量描述运动的耦合，定义耦合率为最大非期望位移除以每个自由度运动的期望行程。表4列出了工作空间实验的结果，其中要求距离是光学系统所需的行程。可以看出，在第二种控制模式下，LVDT传感器的行程限制了运动范围(运动行程等于位移传感器的测量范围)。考虑到安全性，在第一种控制模式下，每个自由度的运动都被驱动到相同的范围。需要注意的是，其实际最大行程均大于表4所列的值。在第二种控制模式下，耦合运动明显受到限制。特别是当X和Y旋转时，解耦率近似等于其他自由度的解耦率。

4.2 位置分辨率测试

定位平台的分辨率是定位平台最重要的指标。众所周知，迟滞效应是压电材料的一个固有问题。目前，有3种常用方法可以对其进行补偿，即基于迟滞模型的前馈控制、基于位置反馈的闭环控制，以及前馈反馈控制相结合的混合控制。该系统采用基于PID控制策略的反馈控制对迟滞进行抑制。由于定位平台的中心位置被镜面占据，位移传感器的测头沿Z轴接近运动平台的顶面。在闭环控制下，定位系统输入阶梯驱动信号。定位平台能够输出的最小步长被认为是分辨率。图16给出了每个自由度运动的对应输出。

(a) X 轴位移

(b) Y 轴位移

(c) Z 轴位移

(d) X 轴转动

(e) Y 轴转动

(f) Z 轴转动图16 各个自由度的分辨率Fig.16 Resolution of each degree of freedom

表4列出了分辨率的实验结果。可以观察到X轴、Y轴的最佳分辨率是0.5μm，Z轴是1μm，旋转运动的分辨率可由三角函数计算而得。

表4 分辨率实验结果

5 结 论

本文提出了一种串并混联的、由压电陶瓷(PZT)驱动的六轴高精度定位系统。采用桥式放大器对PZT行程进行放大，利用柔性铰链消除运动过程中的摩擦和间隙，同时实现了大行程和高分辨率。分析了放大器在两种外部负载下的性能，并根据实际应用情况对放大器进行了设计。此外，还发现在执行机构的输出端必须使用位移传感器，以消除柔性机构中常见的输入耦合现象。设计的可行性通过了有限元分析和实验研究验证。