脉冲推力轨道拦截可达性描述及求解方法*
2019-09-09张洪波
李 彬,郑 伟,张洪波
(国防科技大学 空天科学学院·长沙·410073)
0 引 言
轨道拦截问题是一种典型的空间对抗问题。为了实现对目标航天器的有效拦截,必须合理规划拦截航天器的转移轨道,使其与目标航天器在同一时间到达同一位置。传统的航天器轨道机动任务设计均是在假设机动任务可实现的前提下进行的。如果在设计过程中发现不能满足任务要求,需再进行迭代设计,在这方面表现比较突出的是航天器燃料约束下的轨道机动设计。由于航天器携带的燃料有限,因此航天器在空间的可达范围也是有限的。如果能够事先确定航天器实施空间机动的可达范围,则能够为航天器轨道机动任务的实现提供可行性判据,为轨道机动任务的规划、设计与实施提供有益的支持,从而使得任务设计省时省力,提高航天器任务规划的智能自主能力[1-2]。目前关于轨道拦截任务规划的研究主要可分为两部分,即拦截的最优性和拦截的可行性。
关于拦截最优性研究,研究人员针对轨道拦截快速响应的特点及燃料最优的需求,研究了最短时间拦截和最省燃料拦截问题。John等[3]研究了轨道拦截初制导问题,提出了在燃料约束下两点之间的最短时间拦截问题的求解方法,并将该问题转化为求解一元四次方程的实根;Vinh等[4]研究了一般性的时间约束下的最省燃料拦截问题,并讨论了该问题最优性的必要条件和横截条件;Zhang等[5]研究了燃料约束下的切向脉冲最短时间拦截问题。该方法针对共面拦截问题,利用数值优化方法得到了考虑停泊等待的全局最短时间。
关于拦截任务规划的可行性研究,针对拦截航天器对目标轨道的可达性,研究人员提出了拦截可达范围的概念。常燕等[6]研究了航天器单脉冲变轨与目标航天器交会的机动问题,用追踪区的概念描述了航天器在初始轨道上的可变轨弧段;在此基础上,陈茂良等[7]针对天基拦截器提出了攻击区和威胁区的概念,并利用遍历搜索方法确定了攻击区和威胁区的范围;徐加瑞等[8]也对脉冲变轨的追踪区和机遇区进行了研究,基于Lambert定理,提出了考虑最大变轨能力约束的数值解法;武健等[9]针对初始轨道为圆轨道和椭圆轨道的不同前提研究了拦截器单脉冲作用下的覆盖范围。上述文献所描述的追踪区和攻击区的概念较为相似,均为停泊轨道上的航天器在任务约束条件下能够实现的任务的特殊弧段。
雪丹等[10-12]进一步研究了航天器的空间可达范围。与此前的工作相比,该可达范围仅考虑了航天器的初始轨道状态和机动能力的影响,不再考虑具体的拦截目标及时间约束,表明了航天器在燃料约束下的最大轨道覆盖区域。航天器可达范围的主要应用包括服务航天器对目标航天器的可达性分析和空间安全分析。一方面,通过研究服务航天器的可达范围,可以判断在一定燃料约束下服务航天器可提供的服务的范围,并以此来设计转移轨道,这对于航天器转移轨道的快速设计有着重要的意义;另一方面,其应用可以拓展到轨道拦截的可达性判断。理论上而言,一旦目标进入拦截器的可达范围,目标即存在一定的概率被拦截。这一特性使得可达范围的研究成果可用于拦截任务的可行性预判,也可用于对危险目标进行规避预判。
在航天器空间可达范围概念的基础上,Li等[13]研究了两类脉冲下的航天器轨道的可达区域,该方法的计算结果与雪丹的计算结果一致。在分别考虑各向同性和各向异性速度增量的条件下,Wen等[14-16]研究了航天器单脉冲空间可达范围的精确计算方法。Duan等[17]提出了一种快速、精确的方法,用于确定航天器的可达域,该方法能够以较低的计算复杂度实现相对精确的结果,能够适用于在线和实时应用。以近地空间环境为研究背景,Chen等[18]研究了航天器经过天体引力辅助之后的可达域,使得可达范围分析能够适用于更为广泛的深空飞越任务。此外,不确定性条件下的航天器相对运动可达性,也得到了一定程度的研究[19-21]。
在可达范围概念的基础上,根据拦截器和目标器在不同时刻的位置特点,本文系统定义了拦截航天器的可达范围,随后基于航天器空间可达范围提出了拦截航天器对目标航天器轨道的潜在命中区计算方法;并进一步以轨道面交叉点为命中点,基于共面变轨、逆轨拦截假设,研究了拦截任务的可拦截区和可发射区的计算方法。仿真分析表明该方法能够快速有效地计算出航天器的拦截可达范围,能够用于确定共面变轨、逆轨拦截任务的拦截机会和发射窗口,丰富了面向目标可达范围的应用场景。
1 基本概念
脉冲推力轨道拦截任务的可达范围是一种典型的面向目标的可达范围,根据拦截航天器在对目标航天器实施拦截过程中初始状态和终端状态的关系,可以用命中区、可发射区和可拦截区三种集合来描述轨道拦截任务的可达范围[22],如图1所示。

(a) 命中区

(b) 可发射区和可拦截区图1 轨道拦截可达范围示意图Fig.1 Diagram of reachable domain for orbit interception
下面分别介绍其具体定义。
(1)命中区
给定拦截航天器的初始状态及目标轨道参数,在最大变轨能力和最大任务时间等约束条件下,拦截航天器通过变轨所能到达的目标轨道上点的集合被称为拦截航天器的命中区。命中区是位于目标轨道上的点或弧段,可表示为集合H={φob}。
(2)可发射区
给定拦截航天器的初始轨道参数及目标轨道参数,在最大变轨能力和最大任务时间等约束条件下,在初始轨道上,拦截航天器能够对目标航天器进行拦截的初始位置集合被称为拦截航天器的可发射区。可发射区是位于拦截航天器初始轨道上的点或弧段,可表示为集合L={φM}。
(3)可拦截区
给定拦截航天器的初始轨道参数及目标轨道参数,在最大变轨能力和最大任务时间等约束条件下,在目标轨道上,能够被拦截航天器拦截的目标航天器在初始时刻所在的位置集合被称为拦截航天器的可拦截区。可拦截区是位于目标轨道上的点或弧段,可表示为集合I={φT}。
2 拦截命中区分析
航天器轨道拦截任务的命中区分析是在航天器单脉冲空间可达范围的基础上进行的。航天器单脉冲空间的可达范围可描述为:一个具有施加任意方向脉冲能力的航天器,在单脉冲机动下所有可能到达的位置点构成的集合。显然,该可达范围在惯性空间中为一个三维区域,航天器的空间可达范围也可描述为一系列轨道的集合。为了便于描述航天器的空间可达范围,引入了空间曲面包络的概念[12],航天器的可达范围为该空间内外包络所围成的区域构成,如图2所示。目前,关于航天器单脉冲空间可达范围的计算已有较为成熟的方法[10-12,14-15,17]。

图2 航天器空间可达范围示意图Fig.2 Diagram of reachable domain for spacecraft
航天器的空间可达范围描述了单脉冲轨道机动在惯性空间中的覆盖区域;如果航天器为轨道拦截器,则其可达范围即为拦截航天器在惯性空间中的攻击覆盖范围。当给定一条目标轨道时,若拦截航天器的可达范围与目标轨道存在交集,则表明拦截航天器可对目标轨道特定区域实现覆盖。拦截航天器的可达范围与目标轨道的交集用命中区来进行描述,该命中区为目标航天器轨道上的一段或两段弧段。下面将结合具体的目标轨道分析拦截航天器对给定目标轨道的可达性,并给出拦截航天器对目标轨道命中区的计算方法。
拦截航天器的命中区计算实际上是在航天器的空间可达范围的基础上进一步考虑了目标轨道约束,所以需要首先给出空间包络方程和目标轨道方程的参数化表达形式。下面首先定义计算需要用到的坐标系。
惯性坐标系OE-xyz的定义:以地心OE为坐标原点,x轴方向与初始轨道偏心率矢量方向e0一致,z轴垂直于初始轨道面并指向角动量方向,y轴由右手法则确定。该坐标系用于描述航天器空间可达范围包络在惯性空间中的位置,如图3所示。

图3 Q点在坐标系中的位置表示Fig.3 The position of point Q in the coordinate system
地心惯性系OE-XIYIZI的定义:以地心OE为坐标原点,基本平面为J2000.0地球平赤道面,XI轴在基本平面内由地球质心指向J2000.0的平春分点,ZI轴为基本平面的法向,指向北极方向,YI轴由右手法则确定。
设拦截航天器可达范围外包络上的一点为Q,如图3所示,则Q点在惯性坐标系OE-xyz下的描述为
(1)
式(1)中,rq为Q到地心的距离,其表达式为[15,22]
(2)
式(2)中,Δφ为转移轨道面内的地心转移角,其表达式为[15,22]
(3)
式(3)中,μ表示地球引力常数,h表示转移轨道角动量,ξ、η表示Q点的方位角,α表示脉冲在转移轨道面内的投影矢量的方位角,v1r和v1f分别为航天器在被施加脉冲后的径向速度和周向速度,可表示为α的函数,Δi表示初始轨道面和转移轨道面之间的夹角。
根据几何关系tanη=sin(ξ-f0)tanΔi和cosΔφ=cos(ξ-f0)cosη,对式(3)消去ξ、η,可得
(4)
式(4)中,f0表示脉冲施加点的真近点角。
记拦截航天器的轨道根数为[a0,e0,i0,Ω0,ω0,f0],其含义分别为半长轴、偏心率、轨道倾角、升交点赤经、近地点辐角和真近点角。点Q在地心惯性系OE-XIYIZI下的描述为
(5)

(6)
另一方面,记目标轨道上一点的轨道根数为[at,et,it,Ωt,ωt,ft],则目标轨道上任意一点在地心惯性系OE-XIYIZI下的描述为
(7)
式(7)中,rt表示地心距。

(8)
定义状态变量X=[Δi,α,ft]T,令
(9)
则目标轨道与拦截航天器可达范围的外包络交点在F(X)=0时取得,可通过牛顿迭代法求解该方程组,即可得到命中区在目标轨道上的边界值。图4给出了外包络地心距与目标轨道地心距交集的示意图。从图4可以看出,该场景下的航天器单脉冲空间可达范围包络与目标轨道存在4个交点,从而构成了2个命中区(I和II)。利用点到点的最小能量拦截轨道计算方法[23],以命中区内的点为目标点进行遍历求解拦截航天器初始点到目标点的最小拦截能量Δvmin,得到的结果如图5所示。从图5可以看出,在每一个命中区内均存在一个最小拦截能量点,计算表明该最小拦截能量点与两轨道面交叉点几乎一致。这是由于当预设命中点为两轨道面的交叉点时,拦截航天器对目标轨道的拦截为共面变轨,从而可以节省改变轨道倾角的大量燃料。从节省燃料的角度考虑,两轨道面交叉点是一个较好的预设命中点。

图5 命中区内最小拦截能量变化示意图Fig.5 Diagram of minimum intercept energy in the hit region
3 基本拦截问题
前文在考虑脉冲大小的约束下、结合航天器空间可达范围给出了拦截命中区的计算方法,并且发现两轨道面交叉点为较省燃料的命中点。若以两轨道面交叉点为预设命中点,则拦截策略可简化为共面变轨拦截问题。在脉冲推力轨道拦截任务中,最为常见且最为简单的是初始轨道和目标轨道均为圆轨道的情形,后续分析将基于圆轨道进行假设,仅考虑命中点为两轨道面交叉点的情况,考虑能量、时间及交会角约束分析可拦截区和可发射区的求解方法。
根据轨道拦截任务可达范围的定义,在已知拦截航天器初始状态和命中点的前提下求解拦截任务可拦截区和可发射区(以下统称拦截可达范围),需要分析各种约束对拦截可达范围的影响的特性。
首先,需要分析能量约束对拦截可达范围的影响的特性。最大能量约束决定了航天器的空间可达范围,即决定了拦截航天器可否到达某一高度的目标点,可通过最小能量拦截问题进行判断分析;然后,分析时间约束对拦截可达范围的影响特性。轨道拦截任务时间为拦截航天器调相等待时间与转移轨道飞行时间的和,由于最大任务时间的限制,拦截航天器需要在能量消耗、调相等待时间及转移轨道选择方面进行合理搭配。可通过最短和最长时间拦截问题、固定时间拦截问题及能量给定下的最短时间拦截问题,分析转移轨道飞行的时间特性。通过能量给定下的最短等待和最长等待拦截问题,以及固定任务时间下的最短等待和最长等待拦截问题,分析调相等待的时间要求;最后,分析交会角约束对可达范围的影响特性。交会角影响了拦截航天器与目标航天器之间的视线角度及相对速度,可通过固定交会角拦截问题及交会角与地心转移角之间的关系进行分析。
根据求解拦截可达范围的需要,表1给出了以下8种基本拦截问题[22]。

表1 8种基本拦截问题

续表
Q1~Q3均为经典的拦截问题,文献[1]和[23]研究了针对它们的求解方法;Q4~Q8为针对考虑能量、时间及交会角约束下求解拦截可达范围而提出的拦截问题,文献[22]对其求解过程进行了详细说明。
4 可拦截区分析
根据可拦截区的定义,若给定拦截器初始轨道参数和目标轨道参数,在考虑能量、时间和交会角约束下,可拦截区由拦截航天器变轨点和命中点的相对位置决定。为了求解多约束下的可拦截区,需将求解过程分为三步:首先,求解点到点的可拦截区,即给定调相时间tw下的可拦截区;然后,求解可实施变轨点的集合,即求解调相时间范围。当拦截航天器调相等待时间在此范围内时,均存在与之对应的可拦截区;最后,根据调相时间范围搜索可拦截区边界,即可确定整个可拦截区的范围。
4.1 调相时间给定的可拦截区计算方法
针对给定的变轨点和命中点,根据不同转移轨道飞行时间可以规划出不同的拦截轨道。根据可拦截区的定义,在初始轨道参数、目标轨道参数及约束条件确定之后,可拦截区只与转移轨道飞行时间有关。根据这个特点,可以求解调相时间给定的可拦截区。求解方法主要包含三步:首先,分析能量约束下命中点的可达性;然后,分析在时间和交会角约束下的转移轨道飞行时间范围;最后,求取飞行时间的交集,即可得到三个约束下的实际飞行时间范围。具体的求解流程如下:
步骤1:求解最小能量拦截问题Q1,得到最小拦截脉冲的大小ΔvQ1。如果ΔvQ1≤Δvmax,则进入步骤2。否则,结束计算;
步骤2:求解最短和最长时间拦截问题Q2,得到最短和最长飞行时间Tt min和Tt max。然后,求解时间区间[Tt min,Tt max]与(0,Tob-tw]的交集,将其记为[Tt low,Tt up]。如果[Tt low,Tt up]≠φ,则进入步骤3。否则,结束计算;
步骤3:求解θ=θmax时的固定交会角拦截问题Q4,得到飞行时间Tθmin和Tθmax;
步骤4:求解时间区间[Tt low,Tt up]与[Tθmin,Tθmax]的交集,将其记为[Tlow,Tup]。如果[Tlow,Tup]≠φ,则进入步骤 5。否则,结束计算;
步骤5:根据命中点在目标轨道上的相位角φc和任务总时间范围[Tlow+tw,Tup+tw],可推算初始时刻目标轨道上的弧段区间[φlow,φup],该弧段区间即为可拦截区。
4.2 调相时间范围的计算方法
从给定调相时间的可拦截区的计算部分可以看出,每一个调相时间均对应着一个可拦截区,因此调相时间范围直接影响着可拦截区的范围。分析调相时间范围的计算方法,对于分析可拦截区的存在性及计算可拦截区的大小有着重要作用。由于任务时间为有限值,调相时间范围必然也是有限的,而且该范围必定位于任务时间范围内。记调相时间的最小值和最大值分别为tw min和tw max,为了降低分析难度,将该问题转换为求解能量和时间约束下的调相时间范围问题,以及能量和交会角约束下的调相时间范围问题。然后,求解它们的交集,即可得到三种约束下的调相时间范围。下面分析调相时间范围[tw min,tw max]的求解方法。
(1)能量和时间约束下的调相时间范围
(a)tw max的求解
由于拦截航天器初始点到命中点的地心角Δfob是确定的,因此拦截轨道地心转移角与调相等待地心角的大小呈反相关性,继而求解最大调相时间即可转化为求解拦截轨道地心转移角的最小值。其求解步骤如下:

步骤2:计算最小地心转移角为Δfmin时的拦截轨道飞行时间ΔtE。若ΔtE≤Tob-tEw max,则tw max=tEw max,停止计算。否则,进入步骤3;

(b)tw min的求解
由于最小调相时间tw min的最小值可能是0,因此首先需要判断调相时间为0时是否满足拦截的要求,若非如此,则分析调相时间不为0的情况。由于当拦截轨道转移角为最大时,对应着调相时间的最小值,此时需要求解考虑调相等待的最大和最小转移角的拦截问题。求解步骤如下:


步骤3:求解调相时间为tEw min时的最短飞行时间Δtmin,令T′ob=Tob;



能量和时间约束下的调相时间范围计算流程图如图6所示。

图6 能量和时间约束下的调相时间范围计算流程图Fig.6 Flowchart of calculating the range of phasing time under energy and time constraints
(2) 能量和交会角约束下的调相时间范围
由于调相时间范围与约束下的拦截轨道地心转移角密切相关,因此求解能量和交会角约束下的拦截轨道地心转移角的最大和最小值,即可得到调相时间范围。求解步骤如下:

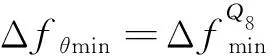
步骤4:若Δfθmin≤Δfob≤Δfθmax,则在能量和交会角约束下的最小调相时间为tθw min=0,最大调相时间为tθw max=(Δfob-Δfθmin)/ni0;
步骤5:若Δfob>Δfθmax(若Δfob<Δfθmin,根据轨道周期性,可转化Δfob=Δfob+2π,即满足Δfob>Δfθmax),最小调相时间为tθw min=(Δfob-Δfθmax)/ni0,最大调相时间为tθw max=(Δfob-Δfθmin)/ni0。
(3) 求交集
在分别求解得到了能量和时间约束、能量和交会角约束下的调相时间范围之后,只需求解它们的交集,即可得到三个约束下的调相时间范围[tw min,tw max],即有
(10)
在能量、时间和交会角约束下的调相时间区间[tw min,tw max]的基础上,即可通过一维搜索算法分别求得可拦截区的最大值及最小值。
5 可发射区分析
根据可发射区的定义,当给定拦截航天器的初始轨道和命中点时,可发射区为拦截航天器初始轨道上的一个弧段,该弧段的大小可由初始轨道上的点相对于命中点(记相位角为φob)的地心夹角范围来描述。为了求解该地心夹角在能量、时间和交会角约束下的范围,结合能量、时间和交会角对拦截轨道地心转移角的影响特性,下面先分别求解能量和时间、能量和交会角约束下的可发射区,然后再计算它们的交集,即可得到三种约束下的可发射区。
5.1 能量和时间约束下的可发射区
能量和时间约束下可发射区的计算步骤如下:
步骤1:计算最小飞行时间Δtmin,如果Tob≥Δtmin,则进入步骤2。否则,停止计算,返回可发射区为空集;

步骤7:可发射区可表示为[φob-Δft max,φob-Δft min]。
5.2 能量和交会角约束下的可发射区
能量和交会角约束下的可发射区的计算方法与能量和交会角约束下的调相时间的计算方法的步骤有相似之处,均是需要先求解能量和交会角约束下的拦截轨道地心转移角的最大和最小值,然后再转化为所需要求解的值。其求解步骤如下:

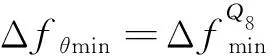
在分别求得能量和时间约束、能量和交会角约束下的可发射区之后,只需要求解它们的交集,即可得到三种约束下的可发射区。
6 仿真分析
6.1 可拦截区仿真
假设拦截航天器的初始轨道高度hi0=400km,初始相位φi0=200(°);目标航天器的轨道高度hob=2000 km,命中点相位φc=0(°);两轨道均为圆轨道,轨道面夹角ξ=20(°);拦截航天器的最大变轨能力为Δvmax=500m/s,最大交会角约束θmax=20.4(°),最大任务时间约束Tmax=2900s,地球半径为Re=6378.137km。
利用调相时间范围计算方法计算得到调相时间的范围为[0, 480.4075s];利用可拦截区计算方法计算得到可拦截区的相位区间为[223.2056(°), 229.6058(°)],目标轨道上的可拦截区示意图如图7所示。

图7 可拦截区示意图Fig.7 Diagram of intercepting region
图8给出了调相时间范围为[0, 480.4075s]时的可拦截区上下边界的变化曲线。从图8中可以看出,随着调相时间tw的增大,可拦截区上边界曲线单调递减,可拦截区下边界曲线先保持不变,然后单调递增;两条曲线的共同作用使得当调相时间为tw min时,可拦截区的范围最大。当调相时间为tw max时,可拦截区的范围缩小为一个点。
图9给出了调相时间与拦截任务总时间的对应关系。外侧虚线表示不同调相时间下能量约束对拦截任务总时间的限制作用,内侧实线分别表示时间约束和交会角约束对拦截任务总时间的限制作用。对比图8和图9,可以看出时间约束边界对应可拦截区的下边界;交会角约束边界对应可拦截区的上边界,并且当调相时间较短时,最大任务时间约束对可拦截区的下边界起到了主要的约束作用,从而使得可拦截区的下边界在一定调相时间范围内可保持不变。
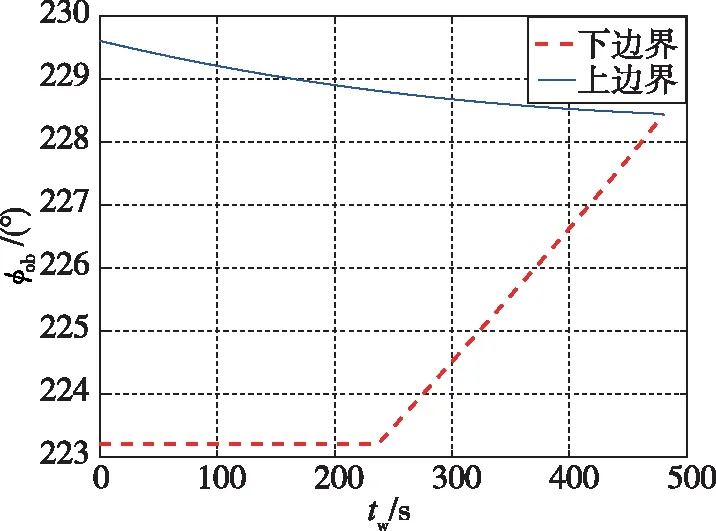
图8 调相时间与可拦截区的关系图Fig.8 Diagram of phasing time and intercepting region

图9 调相时间与任务总时间的关系图Fig.9 Diagram of phasing time and total task time
6.2 可发射区仿真
可拦截区的仿真条件与前述可发射区的仿真条件相同,只是此时拦截器的初始相位不再是给定值,而是需作为可发射区进行求解。利用可发射区计算方法计算得到的可发射区的相位区间为[191.3257(°), 231.1413(°)],可发射区的示意图如图10所示。

图10 可发射区示意图Fig.10 Diagram of launching region
图11和图12分别给出了考虑不同约束组合时的最小能量和最小时间随可发射区相位角的变化曲线。从图中可以看出,最大能量、最大时间和交会角约束对可发射区均起到了限制作用。随着可发射区相位角的增大,拦截能量也不断增大。在可发射区为180(°)附近,拦截脉冲达到了最小,但此时的最小任务时间较长,这与此时霍曼变轨燃料最为节省的结论保持了一致。

图11 可发射区内的最小拦截能量Fig.11 Minimum interception energy in the launching region

图12 可发射区内的最短拦截时间Fig.12 Minimum interception time in the launching region
7 结 论
本文研究了脉冲推力作用下的共面变轨、逆轨拦截任务航天器的拦截可达性问题。首先,基于航天器单脉冲可达范围计算了燃料约束下拦截器对目标轨道的命中区。分析结果表明,两轨道面交叉点为拦截任务燃料的最省点;基于此结论,以轨道面交叉点为命中点分析了共面变轨、逆轨拦截任务的可拦截区和可发射区的计算方法,计算过程考虑了拦截器的调相等待,以及燃料、时间和交会角约束。通过求解不同约束的组合问题,得到了部分约束下的拦截可达范围。然后,计算了它们的交集,得到了三种约束下的拦截可达范围,从而降低了问题的求解难度。仿真分析表明了该方法的有效性,本文所考虑的三种约束均对拦截可达范围产生了影响。针对不同的约束条件,拦截可达范围也将发生变化。该计算方法能够用于分析共面变轨、逆轨拦截任务的拦截可达范围,丰富了面向目标可达范围的应用场景。
