预制混凝土梁吊点处应力集中效应的讨论

任 彧 徐沛韬

(福建省建筑设计研究院有限公司 福建福州 350001)

0 引言

现行国家规范对于预制混凝土构件吊点的设计要求较为简略，设计手册对于吊点的设计细节也未涉及。在工程实践中，设计人员通常将预制混凝土梁简化为一维杆件，按照结构力学和材料力学的经典公式进行验算。实际上，由于吊点的局部作用，会导致在在吊点区域的应力集中。如果预制梁的几何尺寸较大，吊具点处的局部应力可能会超过混凝土的抗拉强度，从而导致混凝土开裂。

当前国内对于预制混凝土构件的研究，主要集中在复杂节点的受力性能以及装配式结构整体抗震性能等方面，对于预制混凝土构件吊装开展的研究相对较少。黄荣[1]根据工程力学知识对预制混凝土预制构件吊点合理位置进行了研究；冯国祥[2]通过理论分析了吊点附加弯矩对预制梁吊装应力的影响，提出了考虑吊装附加应力的必要性以及合理吊点位置的确定方法。但上述工作对于预制混凝土梁在吊装阶段受力性态的研究尚不充分。

然而，在目前工程实践中发现，部分预制混凝土梁由于不合理的吊点设计导致构件在安装阶段开裂，影响预制混凝土构件的力学性能和使用寿命。因此，有必要对预制构件吊点的应力集中问题进行分析。本文的研究主要集中在预制混凝土梁式构件上。

图1 预制混凝土梁

1 计算模型的确定

在工程实践中，预制混凝土梁(图1)通常采用带悬伸段的起吊方案。合理的吊点布置可以使得吊点处的最大负弯矩值与跨中部分的最大正弯矩值相等。当2个吊点对称布置在构件两侧时，吊点距离构件端部0.207L为最佳位置，如图2所示。

图2 两点起吊的预制梁示意图

本文拟采用有限元法进行分析，为控制计算规模，并考虑实际工程情况，计算对象取吊点两侧挑长为2.5倍梁高的对称区域。计算对象如图3所示。

图3 预制混凝土梁模型计算示意图

2 建立有限元模型

基于ABAQUS软件是国际知名的有限元分析软件，其丰富的单元库和其强大的相互作用模拟机制对于研究钢筋混凝土构件力学问题适应性较好，所以，本研究采用ABAQUS软件建立有限元计算模型。

根据指导工程实践的原则，本文算例在梁截面尺寸上选取了20个常见组合，取值如表1所示。计算条件如下：混凝土强度等级 C30，吊具采用Q235型钢，边界条件为梁端部设置X向与Y向的平动约束，在吊点位置的单元4个角点处设置Z向平动约束，其中吊点位置的单元大小为20mm。

表1 预制混凝土梁算例截面尺寸 mm

本文主要研究预制梁在起吊阶段避免开裂的问题，因此不考虑材料的塑性性能。混凝土单元与钢筋单元均选用C3D8R单元，即线性减缩积分8节点六面体三维实体单元。在模拟中混凝土与钢筋均视为各向同性均质材料。材料力学参数根据现行规范取值。

采用Embedded(嵌入)的相互作用方式，将钢筋部件镶嵌在混凝土实体部件中，靠混凝土部件来约束钢筋部件的自由度。在Assembly模块中对梁进行分区处理后，对整体模型采用结构化网格的方式进行划分网格。

3 验证算例对比

取300×600mm的素混凝土预制梁为算例，进行手算结果和有限元分析结果的对比，以验证模型的正确性。

根据平截面假定，支点处由重力荷载引起的弯曲正应力σ可由以下公式得到：

(1)

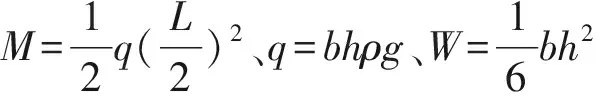
当L=5h时，经计算后可得：

=0.276N/mm2

(2)

由推导结果可知：最大正应力σ与梁高h和材料密度ρ正相关。

建立相应的ABAQUS模型，分别将约束条件设置为：

①梁截面中性轴处的线约束；②梁上表面处的线约束；③梁上表面中点处的点约束。

图4给出了不同约束条件下沿梁高度方向的正应力曲线。

图5给出了点约束条件下的全截面正应力分布。

图4 不同约束情况下的梁高度方向正应力分布图

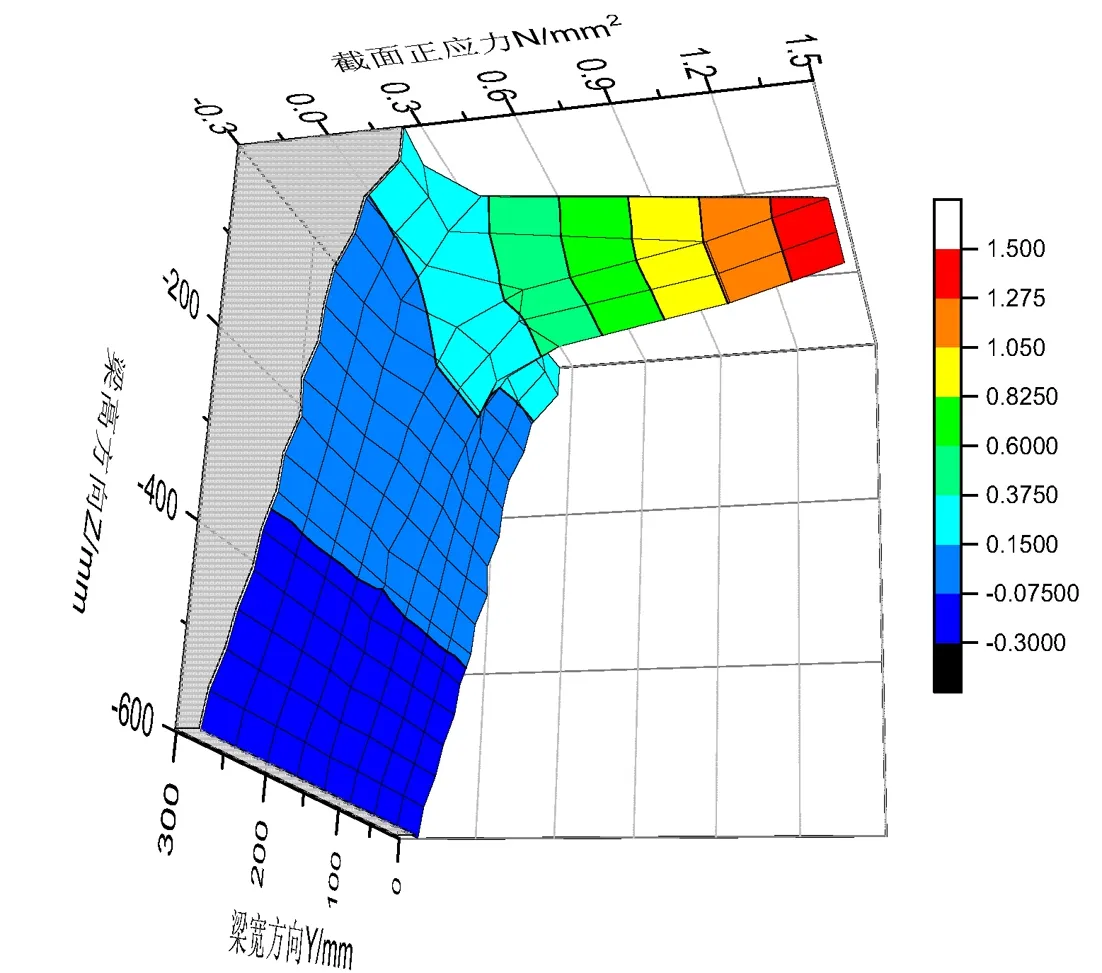
图5 上表面点约束时最大弯矩截面正应力分布图

由图4～图5可知，当约束布置在中性轴处时，计算得到的峰值应力为0.261N/mm2，与经典算法的理论结果相差约5%。结果表明：本有限元分析模型的计算精度可以满足工程需要。

同时，计算结果表明：理论算法仅适用于梁中性轴处线支承的情形；当线约束上移至梁顶面时，混凝土梁变形已不符合平截面假定，梁面最大应力约为理论算法的2倍；当梁面约束由线约束变成点约束后，梁表面应力集中效应更加明显。

4 预制混凝土梁吊点有限元计算

4.1 素混凝土梁

首先考察素混凝土梁在梁面点约束下的内力分布情况。根据有限元分析结果绘制出梁宽度方向的正应力分布曲线，并通过积分计算出的截面平均正应力值σa。把有限元分析获得的最大正应力与截面平均正应力值σa的比值定义为应力集中系数r。不同梁截面尺寸下的计算结果汇总如表2所示。

表2 素混凝土梁应力集中系数(r)

计算结果表明，如将预制混凝土梁视为均质弹性体，应力集中系数与梁宽和梁高正相关，应力集中系数的数值在2.8～6.5之间。该结果符合弹性力学中的圣维南原理。

4.2 设置单点吊具的预制梁

在工程实践中，在起吊位置需设置吊具。首先讨论单点吊具的影响。在计算模型中设置1根20×20×100mm的虚拟吊筋，如图6所示。

图6 虚拟吊筋示意图

由于单点吊具的荷载传递效应，有限元结果显示：吊点周边的应力集中度有所降低，吊点位置处的正应力云图如图7所示。

图7 单点吊具的正应力云图

图8～图11给出了不同梁宽条件下增加单点吊具前后的正应力分布曲线对比。

图8 b=250mm正应力分布图

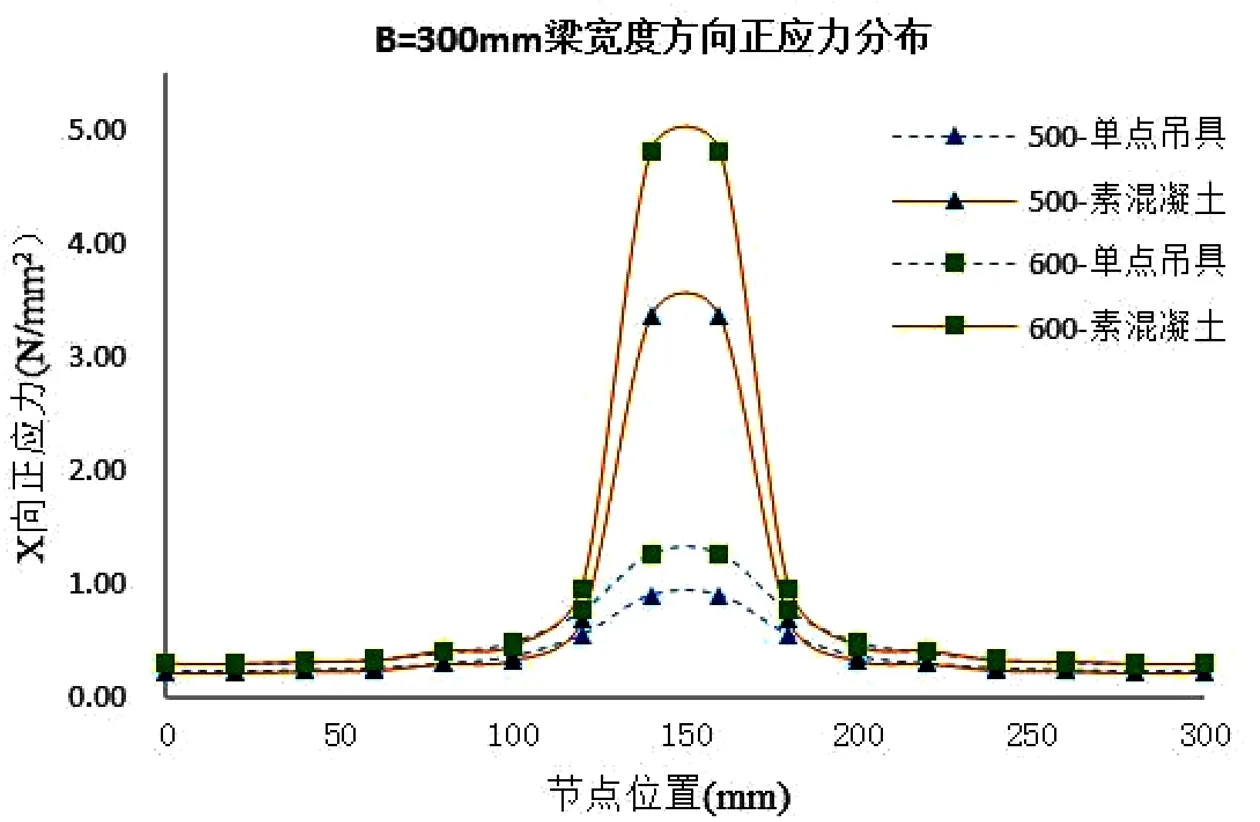
图9 b=300mm正应力分布图

图10 b=350mm正应力分布图

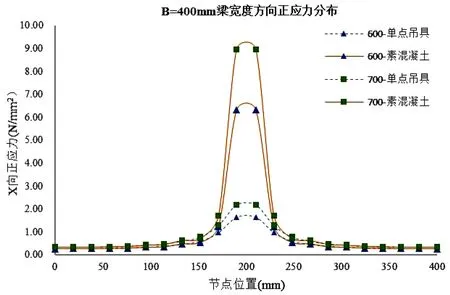
图11 b=400mm正应力分布图

表3～表4给出了增加单点吊具前后混凝土峰值正应力的比值以及应力集中系数r。

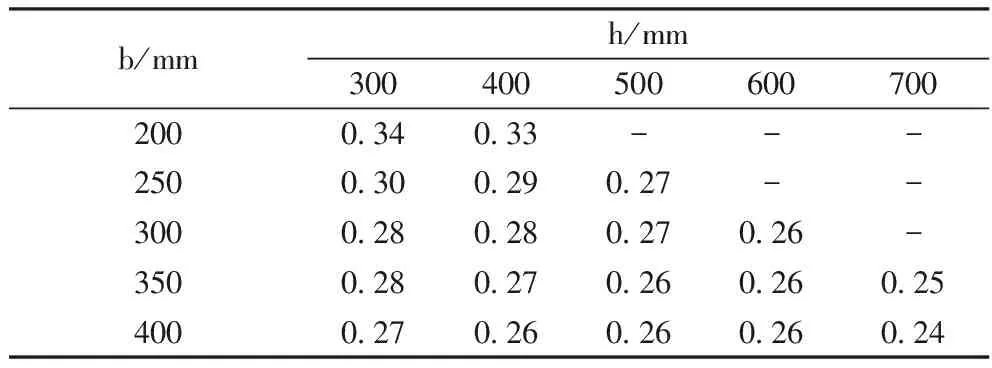
表3 预制混凝土梁加吊筋前后峰值应力比(p)

由图8～图11可知，应力集中区域位于吊点周边各50mm宽的范围。设置单点吊具可显著降低正应力的峰值，降低比例在0.24～0.34之间。

表4 单点吊具的应力集中系数(r)

由图7的正应力云图可知，单点吊具使得高应力区域向梁下部延伸，应力分布较素混凝土梁的集中度低。对比表3～表4可知：设置单点吊具后，正应力沿梁宽方向的不均匀度显著降低，但对于梁宽和梁高较大的预制梁，应力集中系数依然达到了3以上。

为便于讨论，将理论算法得出的最大正应力称为名义正应力；将有限元计算获得的最大正应力与名义正应力的比值定义为应力放大系数P。

由式(1)可知，名义正应力与梁宽无关，表5给出了不同梁高情况下的名义正应力。表6给出不同梁宽和梁高条件下，有限元计算获得的应力放大系数。

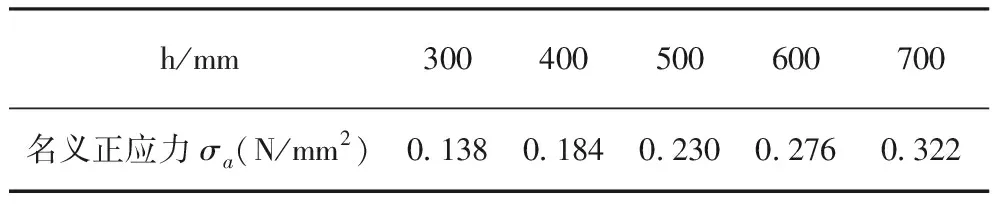
表5 名义正应力σa

表6 设置单点吊具时的应力放大系数(p)

由于存在明显的应力集中效应，当梁宽及梁高较大时，需考虑对预制梁吊点进行加强处理。以下分别对单点吊具两侧设置补强钢筋和采用吊环式吊具两种方案进行分析。

4.3 设置补强钢筋的预制梁

图12 补强钢筋示意图

选取梁宽较大(b=350mm和b=400mm)的两组预制梁，在表层对称设置两个钢筋带，其局部俯视图如图12所示。本节首先考察不同的补强钢筋间距a的对应力峰值的影响,计算结果如图13所示。

图13 梁宽度方向正应力分布图

结果显示：设置补强钢筋后，预制梁正应力分布的峰值有所降低；正应力峰值随着钢筋间距a的增大，呈现出先减少后增大的趋势。针对算例，当补强钢筋间距为a=60mm时，正应力分布曲线的峰值最低，约为无加强筋时的87%。

以补强钢筋间距a=60mm为建模条件，通过有限元计算得出了各种梁截面尺寸在设置补强钢筋前后的峰值应力对比，如表7所示。

表7 设置补强钢筋前后峰值应力比(p)

由表7可知，不同梁宽和梁高的预制梁峰值比均保持在0.87左右，且设置补强钢筋以后，所有算例的应力集中度都得到了改善，应力云图如图14所示。

图14 设置补强钢筋后的正应力云图

4.4 设置吊环吊具的预制梁

当梁宽较大时，预制混凝土梁如采用单点吊具，应力集中度大、容易开裂；这时可以使用钢筋弯曲加工的吊环，构造如图15所示。

图15 单点吊具与吊环构造图

本节选取梁宽为300mm、350mm、400mm的3组预制梁，在梁中部设置虚拟吊环，即以两根20×20×100mm 的棱柱体模拟吊环锚固于混凝土梁中的部分，如图16所示。

图16 虚拟吊环示意图

图17 设置吊环的正应力云图

首先考察吊环沿梁长度方向放置的情形。图17给出了有限元分析的正应力分布。图18～图20给出了不同梁截面尺寸的单点吊具和吊环的正应力分布曲线对比。

图18 300mm梁宽正应力分布图

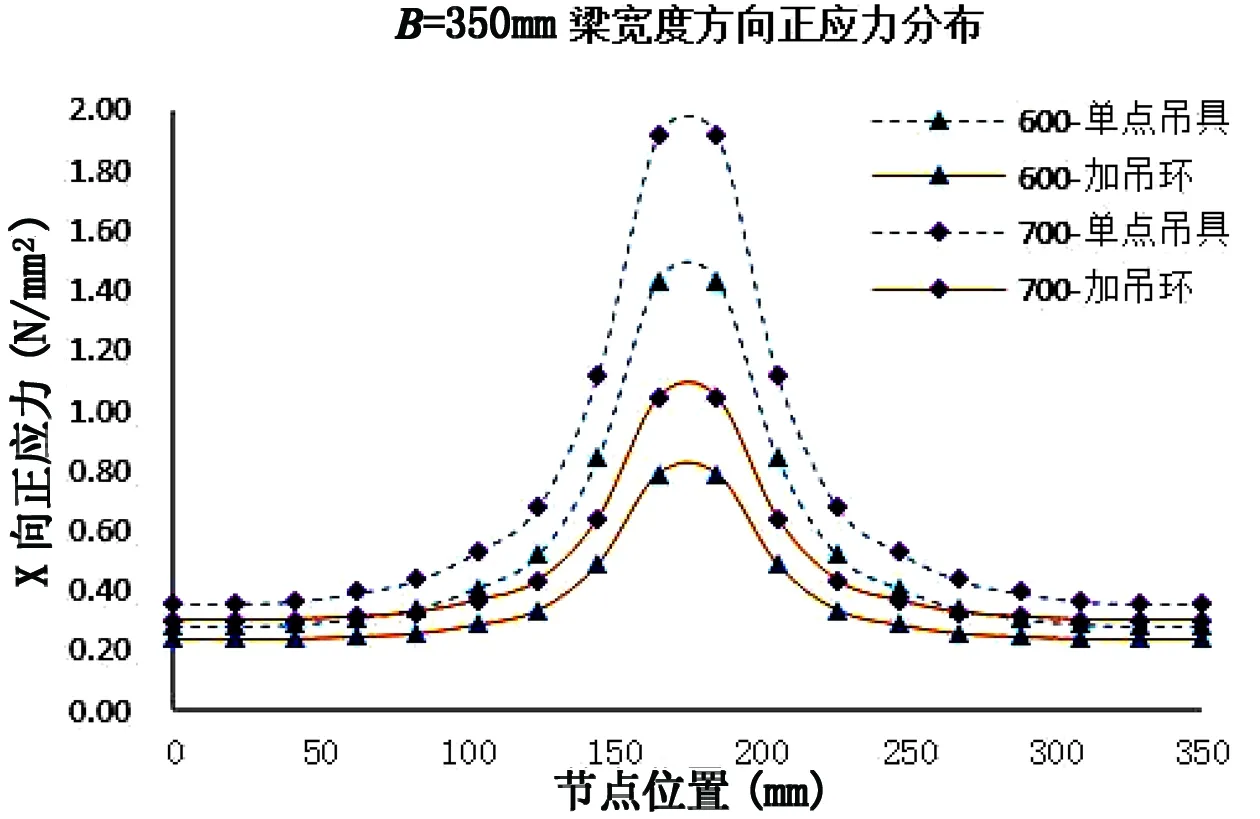
图19 350mm梁宽正应力分布图

图20 400mm梁宽正应力分布图

表8给出不同梁截面尺寸时，吊环与单点吊具的应力峰值比。计算结果显示：改用吊环可以显著降低正应力峰值。

表8 吊环与单点吊具的峰值应力比(p)

其次，考察吊环沿梁宽度方向放置的情形。有限元分析的正应力云图如图21所示，梁截面正应力分布图如图22所示。

计算结果显示：当吊环沿梁宽方向布置时，正应力会在2个吊筋位置形成双峰分布。最大正应力数值和吊环沿梁长度方向布置时相近。

图21 吊环横向放置时正应力云图

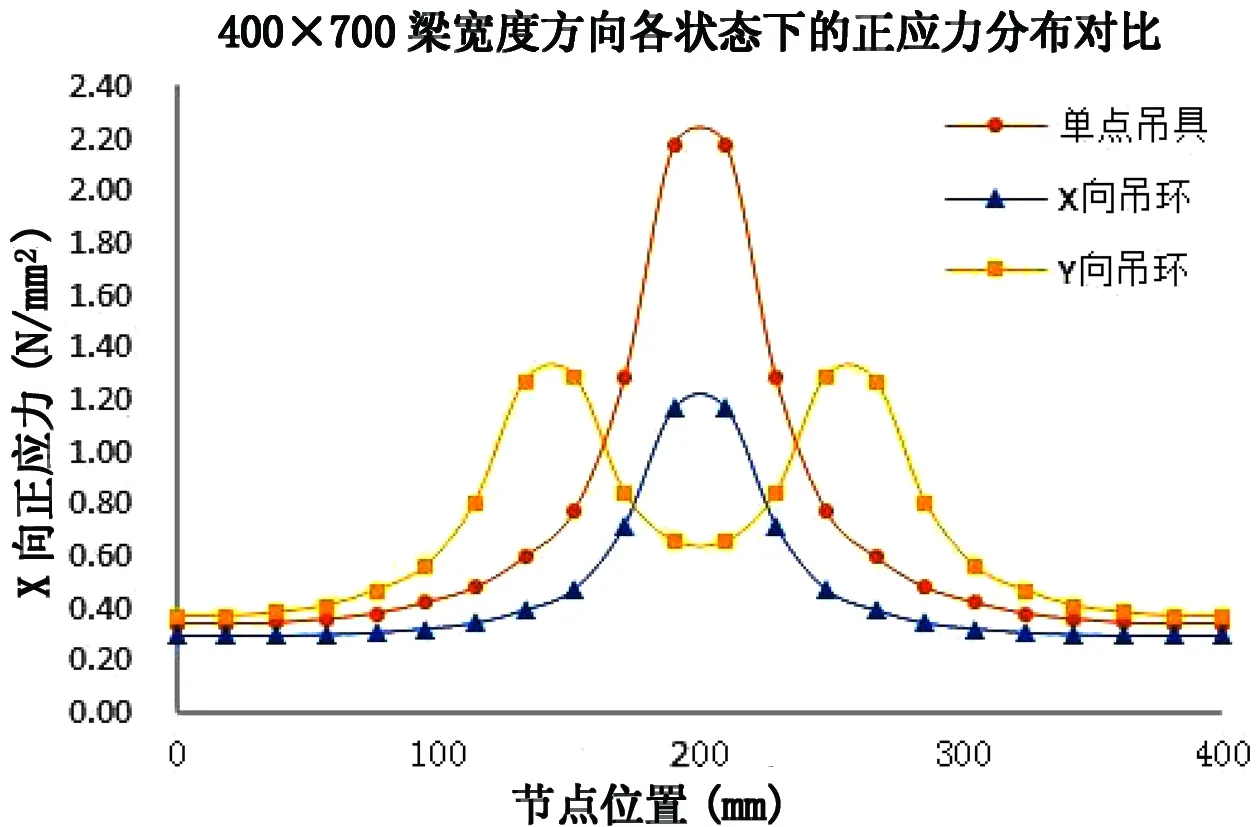
图22 不同吊具时梁截面正应力分布图

5 结论

综上可知：由于吊点处存在显著的应力集中效应，按照结构力学和材料力学的经典公式进行预制混凝土梁的吊装验算，以截面平均最大拉应力进行裂缝控制是偏于不安全的，需要对经典力学公式的结果进行修正。

因此，根据本文进行的近百组有限元分析结果的汇总分析，对于预制混凝土梁开裂验算，笔者建议采用如下公式：

σr=σmη1η2ζ≤ftk

(3)

式中：

σr为考虑吊点应力集中效应的梁面折算正应力；

σm为根据经典公式计算，且考虑吊装动力效应的截面最大正应力；

η1为应力放大系数。

按式(4)计算；

(4)

式中：

b为梁宽；

h为梁高，单位均为mm；

η2为吊具形式修正系数：当采用单点吊具时，取1.0；当采用吊环式吊具时，取0.6；

ζ为加强钢筋修正系数：当在吊具两侧设置加强钢筋时，当钢筋直径不小于D20，且与吊点距离不大于30mm时，取0.9；其余情况取1.0；

ftk为混凝土抗裂强度设计值。