基于PFC2D模拟的矿物粒径非均质效应研究*
2019-09-06韩振华张路青
韩振华 张路青 周 剑
(①中国科学院地质与地球物理研究所, 中国科学院页岩气与地质工程重点实验室 北京 100029)(②中国科学院大学 北京 100049)
0 引 言
岩体作为一种天然的非均质体,由结构面和被结构面包围的岩石块体共同组成。其中,岩石是由一种或多种强度和变形特征不同的矿物构成,矿物颗粒往往会呈现出不同的晶形,并被不同的胶接材料黏结在一起(刘广等, 2013)。岩石与岩体的重要区别就是岩体包含若干不连续面(如:裂隙、节理、层理等),不连续面的存在使得岩体的强度远低于岩石强度。由于细观层次上的非均质性,不同岩石之间强度上也存在很大差异。岩石的非均质性可定义为:岩石在形成过程中受成岩环境、成岩作用和构造作用的影响,物质组成及其结构在空间分布、物理、力学属性等方面的不均匀变化(王香增等, 2016)。岩石物质组成的非均质性主要体现在:矿物颗粒的形态及大小、强度差异及矿物颗粒的接触方式(Lan et al.,2010)。非均质性是导致岩石强度不同的根本原因之一(尤明庆等, 2000; 尹小涛等, 2011),一直以来都是一个重要的研究课题。
岩石作为矿物颗粒的集合体,矿物粒径非均质性对岩石力学特性有很大的影响。一些学者很早就认识到粒径的重要作用,并开展了相应的实验研究。Robina et al.(1996)通过对大理岩单轴压缩实验研究表明岩石峰值强度随粒径增加而减小,并与粒径平方呈反比。Fredrich et al.(1990)对4种不同粒径的大理岩进行三轴压缩实验,发现岩石由脆性向塑性转换所需的围压与粒径成反比。Eberhardt et al.(1999)通过单轴压缩实验分析了粒径对岩石内部裂纹启动和扩展的影响,并指出岩石强度随粒径增大而减小。Sabri et al.(2016)基于巴西圆盘实验研究了粒径对岩体断裂韧度的影响,发现断裂韧度随粒径增大呈现先增大后降低的规律。
还有部分学者利用数值模拟对岩石力学特性进行研究,常用的方法有基于连续介质力学的有限元(FEM)、有限差分(FEM)等和基于非连续介质力学的离散元(DEM)等(魏怀鹏等, 2006)。但岩石非均质性、不连续性及各向异性的特点使得连续介质力学理论在模拟岩石破坏方面有很大局限性。离散元作为解决非连续介质力学问题的重要数值模拟方法更能真实地还原岩石破坏过程,基于离散元理论的颗粒流程序PFC也成为研究岩石类材料的重要工具(周健等, 2000)。一些学者通过PFC数值模拟方法研究了粒径对岩石力学特性影响。Yang et al.(2006)基于PFC2D 模型指出,弹性模量随L/R(L为接触面宽度,R为颗粒平均半径)的增加呈增大的趋势,当L/R大于一定值(L/R>130)时弹性模量增长缓慢并趋于稳定,泊松比随L/R的增大而减小。Potyondy et al.(2004)研究发现,在PFC3D模型中,弹性模量、单轴抗压强度及抗拉强度随粒径的减小均呈增大趋势。还有部分学者研究了模型中粒径分布特征对宏观特性的影响。Ding et al.(2014)研究发现,在模型平均粒径不变的前提下,随粒径比Rmax/Rmin的增加,弹性模量和峰值强度降低,泊松比升高。Koyama et al.(2007)研究表明,即使粒径参数相同,颗粒在模型内随机分布的位置不同,所得到的宏观参数也不同,因颗粒分布状态改变导致的模型宏观参数变异系数随L/R的增加而减小,当L/R>50 时趋于稳定。
已有研究在一定程度上揭示了粒径与材料力学特性之间的关系,但在粒径非均质性方面还缺乏系统的认识。对粒径的研究通常是通过改变平均粒径R或粒径比Rmax/Rmin值来实现,粒径在Rmin~Rmax范围内连续分布。然而实际岩样是由多种矿物组成,不同矿物颗粒的粒径相差很大,如砾岩中粒径大于2imm的颗粒碎屑含量占30%以上,而砂、粉砂等填隙物粒径很小; 花岗岩中钾长石、斜长石粒径可达3imm以上,而云母粒径小于1imm,这说明岩石中矿物颗粒粒径并非连续分布。通过设置不同粒径的组合,本次研究考虑了粒径的非连续分布情况。研究中设计了6种不同的粒径组合方案,以粒径比Rmax/Rmin值作为非均质性的量化指标,旨在研究矿物粒径非均质性对宏观力学特性的影响。由于Lac du Bonnet(LDB)花岗岩是一种很有代表性的脆性岩石,其岩石力学参数全面(Potyondy et al.,2004),常被用来对模型进行对比和校验。以LDB花岗岩为例,作者采用PFC2D 颗粒流程序来模拟岩石单轴压缩破坏,分析了不同粒径组合下的宏观响应,为掌握矿物粒径对岩石强度及变形特性的力学效应提供依据。
1 颗粒流分析法的基本原理
颗粒流分析法通常把离散介质看作是无数颗粒单元的集合体,每个颗粒单元独立运动,单元之间相互接触、相互作用,对非连续介质力学行为的研究就是通过模拟颗粒单元间的这些关系来实现的。如图1所示,颗粒流分析法的基本计算原理为(Cundall, 1971; Cho et al.,2007):(1)根据颗粒单元的位置和半径确定单元相互间的接触关系,采用接触本构模型(力-位移定律)计算接触颗粒单元间的接触力; (2)根据计算得到的接触力,运用牛顿第二定律,计算颗粒单元运动的加速度、速度和位移,更新颗粒单元的位置与相互的接触关系重新计算接触力。如此循环计算,直到试件破坏或满足预定条件,计算结束。

图1 颗粒-黏结系统的受力-位移关系Fig. 1 Force-displacement behavior of grain-bonding system
颗粒流分析法的基本接触模型有3种:接触刚度模型、滑动模型和平行黏结模型。由于平行黏结(图1)可以传递颗粒之间的力和力矩、黏结强度和岩石材料强度有较好的对应关系,因此岩石类材料的细观模拟多采用平行黏结模型。平行黏结模型可以假想为胶结聚合物,颗粒在接触点处胶结在一起,同时黏结物自身受力时,允许产生一定的变形,当接触力超过黏结强度时,黏结破坏。
2 颗粒流模型及计算方案设计
2.1 颗粒流模型的建立
本次研究采用平行黏结模型,模型尺寸为100imm×50imm。首先生成试样模型墙体,确定模型边界,然后通过伺服调节法控制模型的“墙体”运动,模拟加载过程,从而实现单轴压缩模拟试验。根据LDB花岗岩的矿物含量及颗粒特征尺寸(Potyondy et al.,2004),计算出矿物的平均半径为1.2imm(表1)。因此,模型颗粒最小半径取0.8imm,粒径比选为1.66,以保证模型颗粒平均半径为1.2imm。采用“试错法”(徐金明等, 2010)反复改变细观参数,使得模型的宏观力学参数接近LDB花岗岩室内试验力学参数(弹性模量70iGPa、峰值强度224iMPa、泊松比0.26),最终确定的模型细观物理力学性质参数(表2)。校核后,花岗岩室内试验与模型模拟宏观力学参数吻合较好,弹性模量、泊松比和峰值强度分别为70iGPa、0.26iMPa和207iMPa。
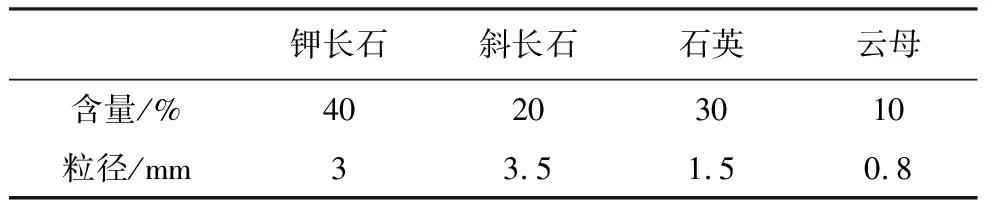
表1 LDB花岗岩矿物含量及粒径Table 1 Composition and average grain sizes of LDB granite
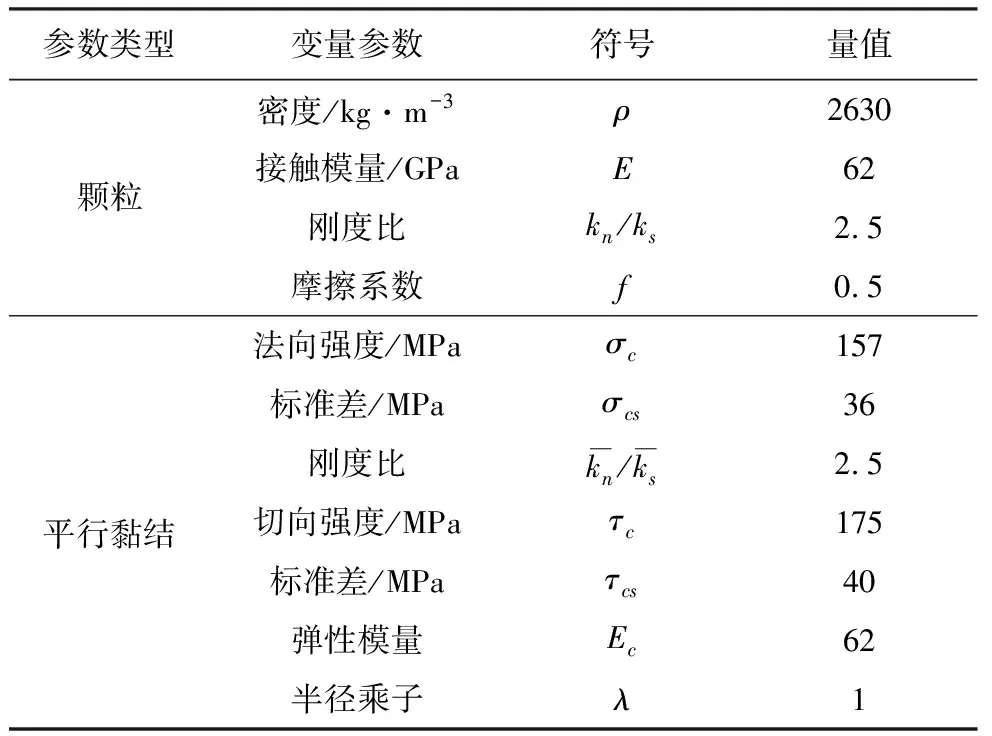
表 2 PFC轴压实验模型细观参数Table 2 Micro physico-mechanical parameters of particle
2.2 计算方案设计
本次研究内容为矿物粒径分布对岩石宏观力学特性的影响。模拟过程中,通过设置不同的粒径组合来体现粒径非均质性。由于岩土材料内部存在颗粒尺寸效应,根据前人研究成果(尹小涛等, 2011),当粒径非常小时,它对模型特性的影响很小,以致可以忽略粒径的作用。但当粒径相对变大时,模型宏观特性受粒径的影响较大。因此,研究中首先采用均质模型分析了颗粒的尺寸效应,为后续非均质模型方案设计提供参考。共设计了一种均质模型及6种非均质模型,具体如下:
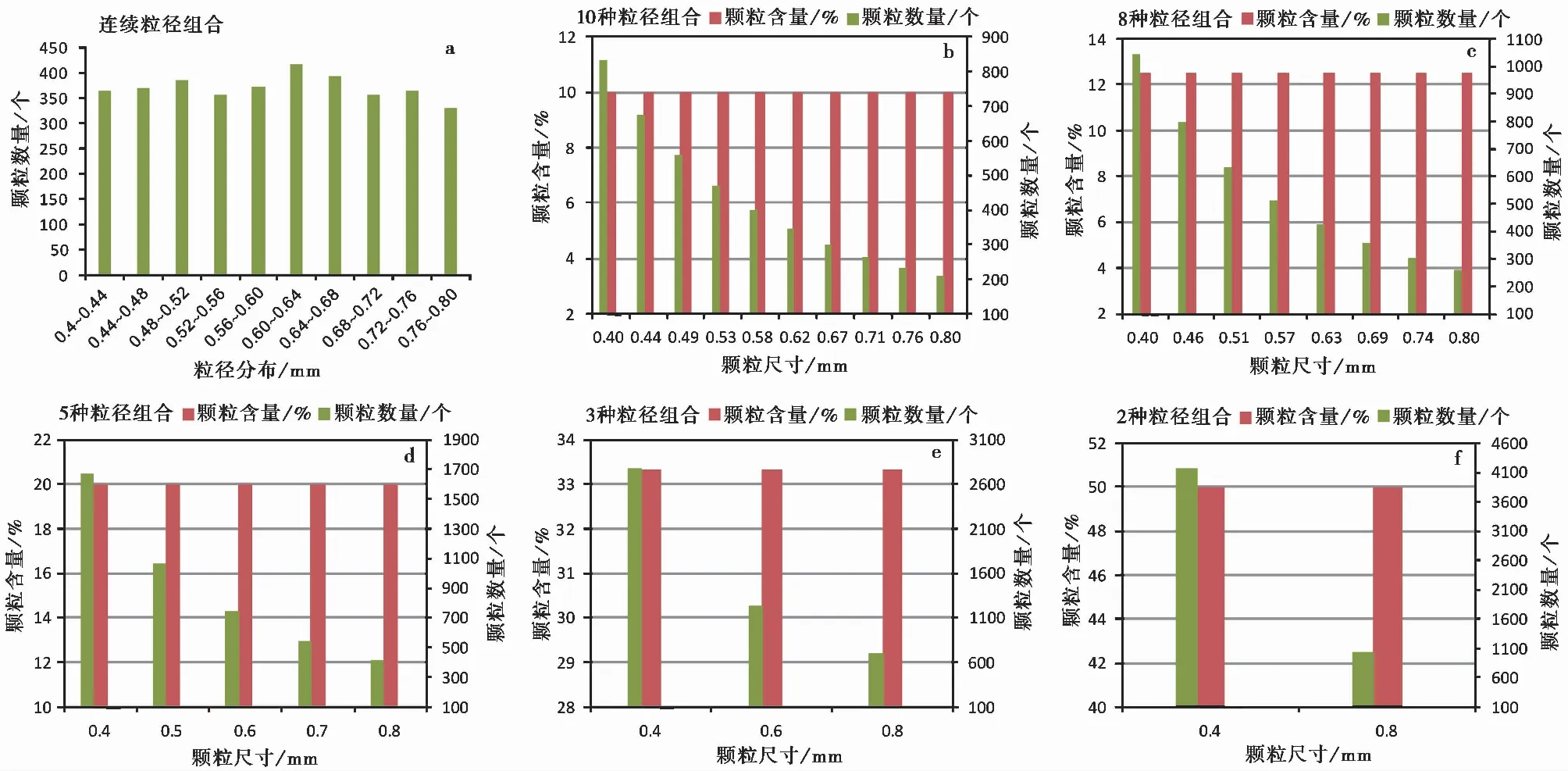
图2 非均质方案1~6中模型粒径分布(以平均粒径0.6imm,粒径比2.0模型为例)Fig. 2 Particle size distribution in scenario 1-6(case study of model with average grain size of 0.6imm and size ratio of 2.0)a. 连续粒径组合-方案1; b. 10种粒径组合-方案2; c. 8种粒径组合-方案3; d. 5种粒径组合-方案4; e. 3种粒径组合-方案5; f. 两种粒径组合-方案6
(1)均质模型:保持模型宏观尺寸及其他细观参数不变,固定粒径比为1,使模型粒径处于均匀分布状态。改变粒径,使其在0.30~2.00imm之间变化,以此来研究模型在均质状态下颗粒的尺寸效应。
(2)非均质模型:共设计6种方案(表3),每种方案下设置5种平均粒径模型,每种平均粒径下设置4种粒径比,最大与最小粒径分布情况如表4所示。不同的方案中粒径的数量不同,即最大与最小粒径之间的过渡粒径种类不同。

表3 6种非均质模型方案Table 3 Six scenarios with heterogeneous grain sizes
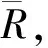
(1)
其中,i为矿物的种类;Ri为第i种矿物的粒径;Ci为第i种矿物的含量。模型的粒径非均质程度用粒径比来表征,粒径比越大,非均质性越强。以平均粒径0.6imm,粒径比2.0的模型为例,在不同粒径组合下模型内部尺寸分布如图2所示。

表4 不同平均粒径、粒径比下模型中的最大与最小粒径Table 4 Distribution of maximal and minimum size in the model with different mean grain size and size ratio
由于模型是由矿物颗粒的随机分布组成的,PFC程序通过选取不同的随机数种子来实现不同的颗粒分布。当粒径参数相同时,采用不同的颗粒分布状态,所造成的模型内部应力分布不同,因此模型宏观特性也是不同的。由颗粒分布状态不同所造成的宏观特性离散化是客观存在的,但可以通过多次模拟取平均值的方式进行宏观趋势化分析。本次研究针对每个模型试验均选取7个随机分布状态,因此,在5种平均粒径、4种粒径比下, 6种设计方案共包含算例840个,主要分析了粒径非均质性对宏观弹性模量、峰值强度及泊松比的影响。弹性模量采用应力为试样峰值强度一半时应力与应变的比值,泊松比采用应力为试样峰值强度一半时侧向应变与轴向应变的比值(尤明庆等, 2003)。

图3 均质模型中粒径及颗粒分布对宏观特性的影响Fig. 3 Effects of particle size and distribution on micro-mechanical properties in homogenous modela. 弹性模量; b. 峰值强度; c. 泊松比
3 模拟结果分析
3.1 粒径均匀分布下的尺寸效应研究
均质状态下,粒径及其分布状态对模型宏观特性的影响如图3所示。首先,模型的平均弹性模量和峰值强度均随着粒径的增大而减小,而泊松比随粒径的增大呈增大的规律,与前人研究成果一致(Potyondy et al.,2004; Ding et al.,2014)。粒径由0.3imm增长到2.0imm时,平均弹性模量降低了20.1%,峰值强度降低了13.4%,泊松比提高了9.4%,说明粒径变化对弹性模量的影响比较明显,其次是峰值强度,对泊松比影响较小。此外,由7组试样模拟结果的标准差(图3)可以看出,由颗粒分布状态的不同导致的模型宏观力学特性离散化程度随粒径的增大而增大。
由图3不同粒径所对应的颗粒总数可以看出,粒径小于0.40imm时,模型颗粒规模将过万,这会导致计算效率低下,而粒径过大则会导致颗粒总数太少,颗粒结构在应力作用下稳定性变差,计算结果的波动也较大。因此,虽然LDB花岗岩矿物颗粒尺寸较大(表1),但在模拟过程综合考虑计算规模和粒径的敏感性,所采用的颗粒平均粒径为0.3~0.7imm。
3.2 粒径非均质性对岩石宏观力学特性的影响
岩石中矿物成分、粒径、空间分布等都对其力学特性有影响,本次设计的6种非均质方案综合考虑了粒径大小、数量及分布的影响。

图4 非均质方案1~6中模型粒径非均质性对弹性模量的影响Fig. 4 Effect of particle heterogeneity on elasticity modulus in scenario 1-6a. 连续粒径组合-方案1; b. 10种粒径组合-方案2; c. 8种粒径组合-方案3; d. 5种粒径组合-方案4; e. 3种粒径组合-方案5; f. 两种粒径组合-方案6
3.2.1 粒径非均质性对弹性模量的影响
图4为粒径非均质性对弹性模量的影响。可以看出, 6种方案中弹性模量随模型平均粒径的增加均呈减小趋势,随粒径非均质性(粒径比)的增加也呈现减小的规律(方案5、方案6除外)。首先,粒径在均质状态下,模型的弹性模量较高,在模型由均质状态向非均质状态转化阶段(粒径比由1变化到1.2阶段),弹性模量呈现明显减小的趋势。随着粒径非均质性的增大(粒径比由1.2变化到2.0阶段)弹性模量继续降低(图4a-4id),但变化幅度较小。
需要指出的是,在3种粒径组合(图4e)和两种粒径组合(图4f)模型中,当粒径比为2时,弹性模量并没有达到最低,反而呈增高的趋势。如图4e所示, 3种粒径组合下粒径比为2时的弹性模量大于粒径比为1.6时的弹性模量; 图4f中, 两种粒径组合下粒径比为2时的弹性模量大于粒径比为1.2时的弹性模量。该变化规律与模型中细颗粒的含量有关,如表4所示,随着粒径比的增大模型中的最小粒径减小,粒径比为2的模型含最小的粒径。在方案5和方案6中,最小粒径颗粒含量分别为33.3%和50%,相比于其他方案,最小粒径的颗粒含量及数量较高。根据对模型均质状态下尺寸效应的研究(图3)可知,粒径越小,弹性模量越大。因此在这两种方案中,粒径比为2时,相比于粒径非均质性对弹性模量的降低作用,细颗粒对其提高作用更明显。
为进一步分析细颗粒对弹性模量的作用,以两种粒径组合为例,取0.4imm和0.6imm两种平均粒径的模型,以0.27imm和0.4imm分别作为两模型中的最小粒径(细颗粒粒径)。模拟过程中,改变模型中细颗粒的含量,以研究细颗粒的作用,分析结果如图5所示。可以发现,随着模型中细颗粒含量的提高,细颗粒数量的增长十分明显,弹性模量呈现先减小后增大的规律。该规律解释了图4e和图4f中弹性模量的变化,弹性模量在初期表现出降低的趋势主要受粒径非均质性的影响,在后期呈现增大的规律主要受细颗粒的控制作用。
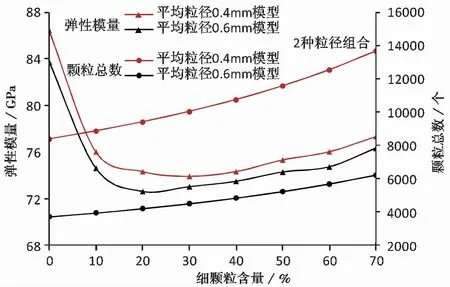
图 5 细颗粒含量对弹性模量的影响(以两种粒径组合、平均粒径0.4imm和0.6imm的模型为例)Fig. 5 Effects of fine particle content on elasticity modulus(case study of model with two kinds of grain size, mean grain size respectively 0.4imm and 0.6imm)
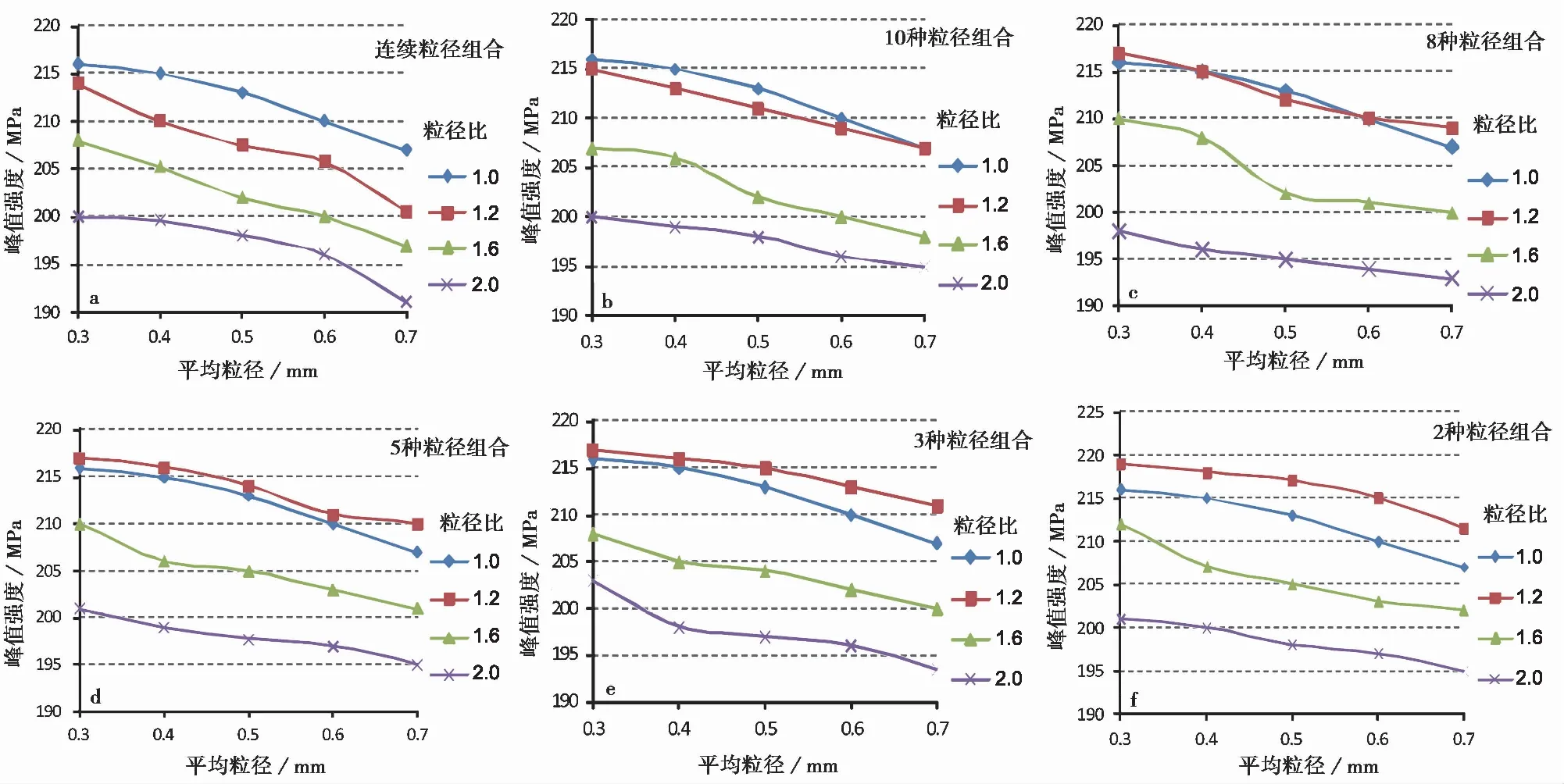
图 6 非均质方案1~6中模型粒径非均质性对峰值强度的影响Fig. 6 Effect of particle heterogeneity on peak strengtha. 连续粒径组合-方案1; b. 10种粒径组合-方案2; c. 8种粒径组合-方案3; . 5种粒径组合-方案4; e. 3种粒径组合-方案5; f. 两种粒径组合-方案6
3.2.2 粒径非均质性对峰值强度的影响
图6为粒径的非均质性对峰值强度的影响结果。可以看出,在6种方案下,峰值强度随模型平均粒径的增加均呈减小的趋势。在非均质状态(粒径比1.2、1.6、2.0)下,随粒径比的增大,峰值强度也呈减小的规律。此外,峰值强度随粒径比的变化规律与粒径组合有关。在连续粒径组合下(图6a方案1),均质状态时模型具有较高的峰值强度,随着模型中粒径种类的减少,粒径比为1.2时的峰值强度逐渐提高(图6b-6f),并超过均质状态下模型的峰值强度。但当粒径比为1.6和2.0时,随着模型中粒径组合种类的减少,峰值强度没有明显增大或减小的规律。这说明,模型在粒径非均质程度不高的情况下,即粒径比较小时,峰值强度受粒径组合数影响较大。

图 7 粒径比对峰值强度的影响(以两种粒径组合、平均粒径0.4imm和0.6imm模型为例)Fig. 7 Effect of size ratio on peak strength(case study of model with two kinds of grain size, mean grain size respectively 0.4imm and 0.6imm)
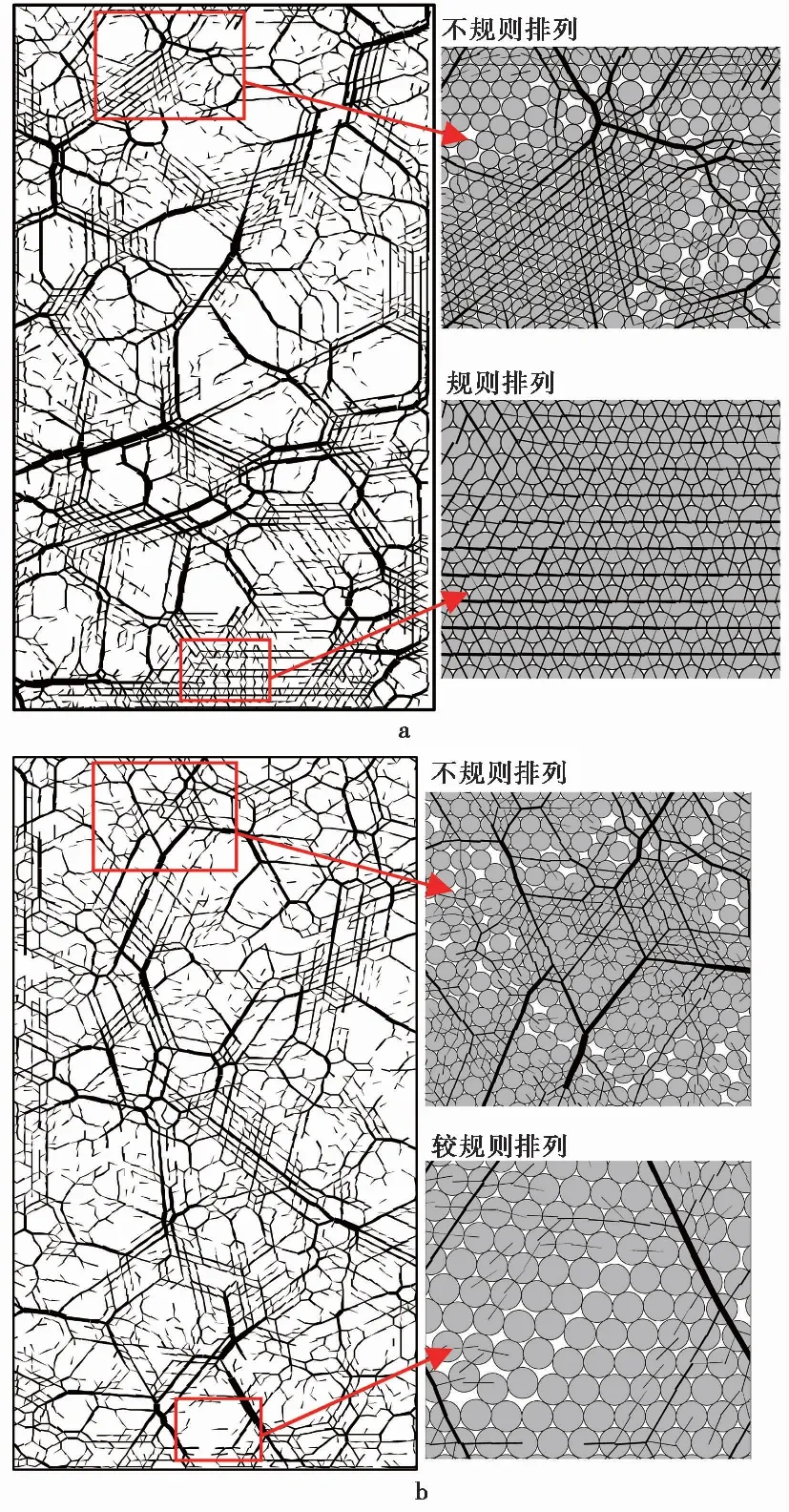
为进一步分析粒径在非均质程度不高时,峰值强度的变化规律。以两种粒径组合(方案6)为例,增加几种粒径比: 1.05、1.1、1.15、1.3、1.4,取0.4imm和0.6imm两种平均粒径的模型,进行模拟结果分析。如图7所示,在模型粒径非均质程度不高的情况下(1.05 图8 方案1~6中模型粒径非均质性对泊松比的影响Fig. 8 Effect of particle heterogeneity on Poisson’s ratioa. 10种粒径组合-方案4; b. 5种粒径组合-方案5; c. 2种粒径组合-方案6 3.2.3 粒径非均质性对泊松比的影响 图8为粒径非均质性对泊松比的影响,可以看出,泊松比受粒径大小及粒径非均质性的影响比较小,但也表现出了明显的规律性。以粒径种类为10、5、2的3种模型为例(图8a~8c),可以看出,不同平均粒径下,泊松比随模型平均粒径的增加均呈增加趋势,随粒径比的增加也呈现出增加的趋势,但变化幅度比较小。当颗粒平均粒径由0.3imm增加到0.7imm、粒径比由1.0增加到2.0,泊松比变化范围在0.23~0.25之间,其他颗粒组合状态下,泊松比也表现了相似的变化规律。 PFC程序可提供两种默认的颗粒生成方式:连续均匀分布和高斯分布。连续均匀分布是指在最大最小粒径之间,粒径是连续的,即本次模拟采用的方案1中的颗粒分布形式,是一种广泛被采用的颗粒分布方式。本次研究,除了考虑粒径连续均匀分布模型外,还增加了多种粒径组合模型,并分析了它们在不同粒径比下的宏观响应。上述颗粒分布指的是一个模型中粒径大小的分布情况,实际上采用相同的粒径参数,当颗粒的随机分布位置不同时,模型的宏观特性也不同(Koyama et al.,2007)。 本文在对粒径均质模型尺寸效应分析的同时,针对每个模型,通过7次随机试验,研究得出颗粒随机位置的不同会导致宏观力学特性的离散化,且该离散程度随粒径的增大而增大。PFC通过选取不同的随机数种子(set random seed)来实现不同的颗粒分布。颗粒在模型内部的分布实际上由一系列的随机数决定,随机数种子就是产生随机数的第一次使用值。颗粒生成机制是通过蒙特·卡罗方法,将种子值转化为随机数空间中的某一个点上,即模型内部的某一位置,以后产生的随机数都与前一个随机数有关。因此,一个随机数种子对应一种颗粒分布状态。 以粒径为0.5imm的均质模型为例。采用随机数种子为51时,模型内局部颗粒分布情况如图9a; 采用随机数种子为9时,在相同位置颗粒分布情况如图9b,两种颗粒分布状态有明显的区别,因此造成了模型内部应力分布的不同,最终导致宏观特性的不同。此外,相比于粒径非均质模型,均质模型具有明显较高的弹性模量(图4),而峰值强度却没有表现出相同的规律(图6),反而低于方案4~方案6中粒径比为1.2的非均质模型峰值强度。该现象与均质模型在二维状态下的颗粒分布状态密不可分,如图9所示,在均质模型中,由于颗粒生成时位置在模型内部是随机分配的。因此,在生成各向同性应力状态的集合体后,颗粒并非全部都规则排列,在颗粒排列不规则的区域容易形成应力集中,力链分布的不均匀性造成了宏观强度的降低。当均质模型内部颗粒完全规则排列时(Lan et al.,2010),其峰值强度会明显高于非均质模型。采用三维均质模型,这种局部颗粒不均匀排列的现象也会明显减小,使得模型峰值强度会有明显的提高(Ding et al.,2014)。 图9 不同随机种子数下模型内部应力分布及局部颗粒排列(以粒径为0.5imm的均质模型为例)Fig. 9 Contact force chain in the model and local grain distribu ̄tion(case study of homogenous model with grain size of 0.5imm)a. 随机种子数51(弹性模量86.6GPa、峰值强度218iMPa); b. 随机数9(弹性模量84.6iGPa、峰值强度200iMPa) 表 5 方案4各计算模型的实际孔隙率Table 5 Final porosity of each model in scenario 4 岩石是一种天然的多孔材料,其内部包含着大量不规则、跨尺度的孔隙,岩石孔隙率的增大会造成宏观弹性模量的降低。本次研究内容为粒径非均质性对宏观的特性的影响,因此模型孔隙率均设为0.16以减少模拟过程的研究变量。但需要注意的是,初始孔隙率仅用来确定生成模型所需的颗粒总数(式(2)),模型在达到应力平衡状态,即生成各向同性应力状态集合体的同时,模型的孔隙率会有所改变。 N=A(1-n)/πR2 (2) 以本次模拟的方案6为例,模型最终孔隙率统计结果如表5所示,可以看出,孔隙率随粒径增大呈增大趋势,同时弹性模量和峰值强度表现出降低的趋势。与设定孔隙率0.16相比,均质模型的孔隙率明显减小,主要原因为均质模型中大部分颗粒处于一种较密实的排列状态(图9),这也是均质模型弹性模量相对较高的原因。不同非均质模型的孔隙率变化幅度较小,因此,粒径比为1.2~2.0时,模型的弹性模量也变化较小。可以看出,粒径对弹性模量的作用机制是通过影响孔隙率实现的。 为进一步分析不同初始孔隙率下,实际孔隙率及宏观特性的变化,以平均粒径0.4imm、粒径比1.2的连续粒径模型为例。如表6所示,当设定的初始孔隙率从0.1变化到0.35(增长250%)时,实际模型在单轴压缩前对应的孔隙率仅从0.151变化到0.164(增长8.6%),随着孔隙率的变化,弹模模量、峰值强度及泊松比的变化趋势如图10所示。 表 6 实际孔隙率、平均粒径及颗粒总数随设定孔隙率的变化(以平均粒径0.4imm、粒径比1.2的连续粒径模型为例)Table 6 Change of final porosity, average grain size and total grain number with design porosity(case study of model with average grain size of 0.4imm and size ratio of 1.2) 图10 孔隙率对模型宏观特性的影响Fig. 10 Effect of porosity on micro-mechanical propertiesa. 弹性模量; b. 峰值强度; c. 泊松比 由图10可知,弹性模型和峰值强度随设定孔隙率的增大呈降低的趋势,泊松比呈增大的趋势,但变化量均较小。宏观特性随孔隙率的变化所表现出的规律,实际上与模型颗粒总数和平均粒径增大有关(表6),初始孔隙率越大,模型颗粒数越少,因此造成的模型宏观强度上的降低。因此,在生成模型时,需要选择一个合适的孔隙率值,使得模型的最终孔隙率与平均粒径能与初始设定值之间的差距最小。本次模拟采用的平均粒径为0.4imm。根据表1,当初始孔隙率为0.16时,模型的最终孔隙率和平均粒径与设定值最接近。因此,在PFC二维模型中,要在给定空间内生成颗粒,既能保证孔隙比和粒径符合要求,又能使组合达到平衡,建议选用的孔隙率为0.14~0.18。 本文基于颗粒流程序PFC2D研究了粒径非均质性对岩石宏观力学特性(弹性模量、峰值强度、泊松比)的影响。通过设置不同种类粒径组合及粒径比来体现粒径非均质性,共设计了6种研究方案,粒径种类分别为:连续、10种、8种、5种、3种、2种,每种方案下设置5种平均粒径模型: 0.3imm、0.4imm、0.5imm、0.6imm和0.7imm,每种平均粒径下设置4种最大最小粒径比: 1.0、1.2、1.6、2.0,每个模型通过变换随机数取7个随机分布状态,进行单轴压缩试验,并得到以下几点认识: (1)弹性模量和峰值强度随模型平均粒径的增大而减小,泊松比随平均粒径的增大呈增大的趋势,由颗粒分布状态所引起的宏观特性的离散程度也会随粒径的增大而增大。 (2)通常情况下,弹性模量随粒径非均质性增大呈减小的规律,但不同非均质模型之间变化范围较小。当模型内部细颗粒含量足够高时,细颗粒对模型弹性模量具有提高的作用,此时细颗粒效应会大于粒径非均质性效应。此外,粒径对弹性模量的作用主要是通过影响孔隙率实现的。 (3)当模型粒径非均质程度不高时,峰值强度随粒径非均质性增大呈增大的规律,主要原因为模型内细颗粒含量也是增大的,细颗粒对模型峰值强度具有提高作用; 随着尺寸非均质性的进一步增大,峰值强度呈现减小的规律,此时粒径非均质性效应大于细颗粒效应。 (4)泊松比随模型颗粒平均粒径的增加均呈增加趋势,随粒径比的增加也呈现出增加的趋势,但粒径大小及粒径非均质性对其影响较小。 (5)利用PFC程序生成模型颗粒时,需要选择合适的初始孔隙率,否则会导致实际生成模型的孔隙率和粒径不符合设定要求。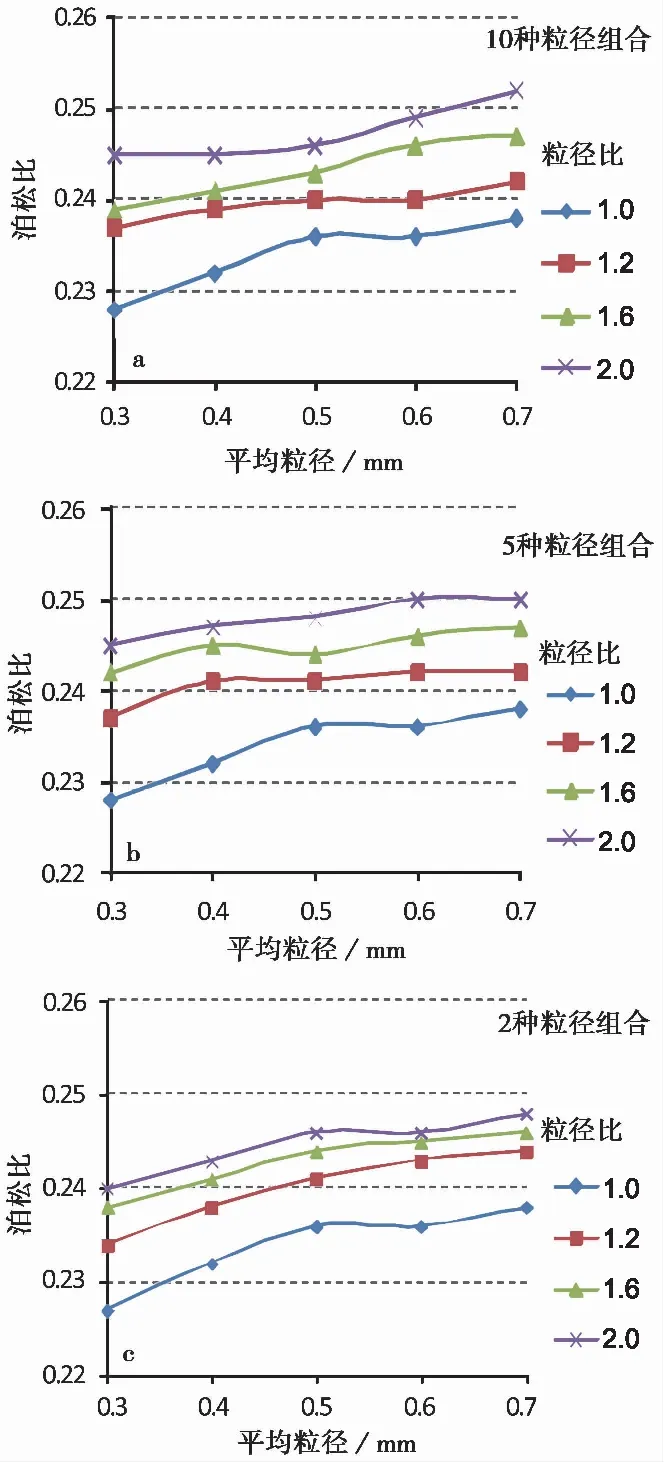
4 讨 论
4.1 颗粒随机分布的影响
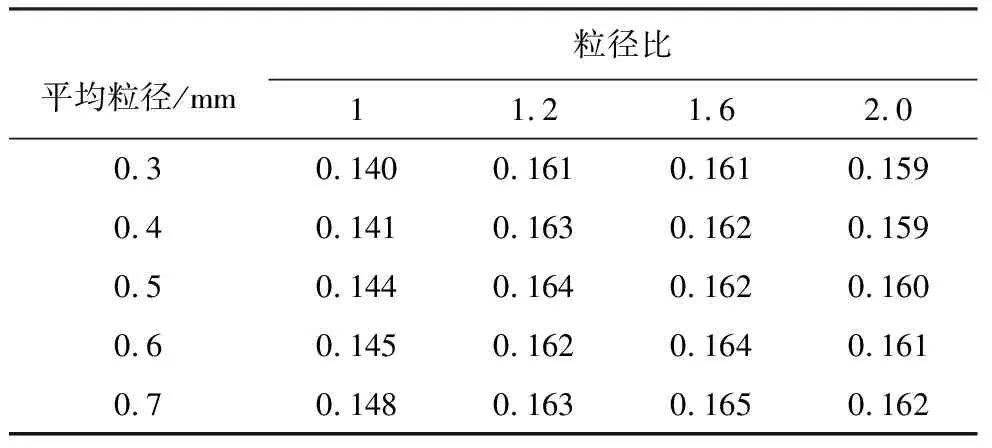
4.2 孔隙率的影响

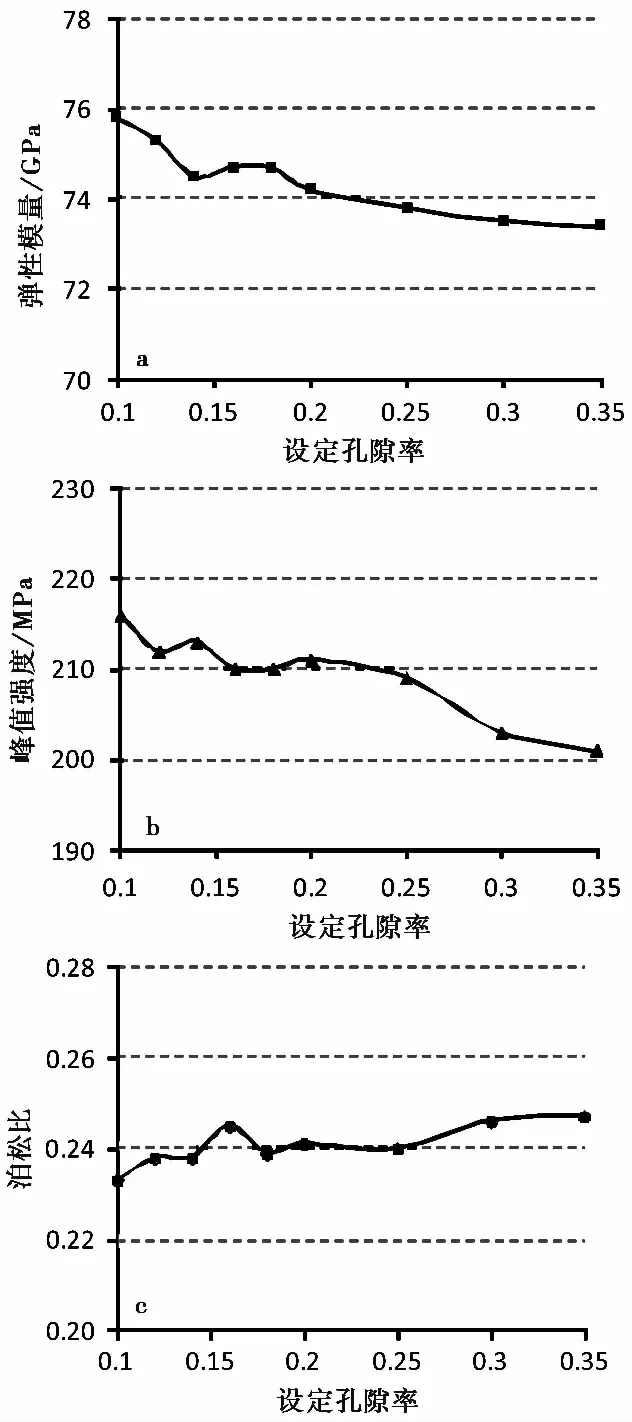
5 结 论
