玄武岩纤维黄土抗剪强度变化规律与最优配合比分析
2019-09-06胡文乐何朋立
胡文乐,何朋立,刘 华
(1.西安建筑科技大学土木工程学院,陕西 西安 710055;2.洛阳理工学院土木工程学院,河南 洛阳 471023)
0 引言
黄土是广泛分布于中国西北地区的一种独特的地质载体,也是亟需处理的工程对象。黄土滑坡作为我国西北地区最为严重的地质灾害,给人民的生命财产安全带来威胁[1],随着地质灾害与防治工程活动的加强,黄土滑坡成为近年来工程地质研究的热点问题[2]。大型滑坡更是以其规模大、机制复杂、危害大等著称[3],近年来出现的边坡失稳、桥梁与建筑物地基破坏、建筑物不均匀沉降等破坏现象,通常采取的措施有:增强排水、压密、加筋、置换等[4]。其中纤维加筋技术是目前土体改良加固,提高土体抗剪强度,预防土体地质灾害问题的常用方法之一。因此,越来越多的研究人员开展了对经济、环保、高效的玄武岩纤维加筋改良固化土体的一系列研究工作[5-7],为滑坡、边坡失稳、地基破坏等复杂地质灾害的预防和防治提供理论依据。
运用加筋技术改善土体受力情况、提高土工结构的强度和稳定性,是现阶段研究的热点问题之一[8]。常用加筋材料中,玄武岩纤维凭借其自身优良的物理和化学性能而闻名[9]。目前将玄武岩纤维掺入土体中的研究较少[10],李广信等[11]通过将纤维添加到黏性土中进行三轴试验,发现玄武岩纤维的加入能够有效提高黏性土的抗剪强度,并且能够增加土体的韧性和塑性;高磊等[12]对玄武岩纤维加筋黏土进行固结不排水(CU)试验,结果表明,玄武岩纤维能够有效增加黏土的黏聚力;王德银等[13]以饱和黏性土为加筋对象,进行一系列直剪试验,并借助电镜扫描技术,发现纤维的加入能够有效提高土体的抗剪强度,而且黏聚力的提高程度优于内摩擦角。至今在玄武岩纤维加筋土研究方面取得的成果较为深入,玄武岩纤维机理的研究越加丰富,但在研究方法上大多运用控制单一变量的试验方法,试验工作量大,试验时间较长,但运用正交试验设计进行三轴试验的研究较少。
本文取6 mm玄武岩纤维作为加筋材料,设计三因素四水平正交试验表,考虑到边坡、地基等实际工程的工况,进行固结不排水三轴(CU)试验,通过极差分析和方差分析,确定最优配合比。并对最优配合比进行不同围压、不同纤维掺量下的三轴试验,研究玄武岩纤维土的应力-应变特性,得出纤维掺量对有效抗剪强度指标的影响。
1 试验内容
1.1 土料
试样为黄土土料经风干、碾碎、过2 mm筛后获得,封存于玻璃罐中备用。土颗粒呈肉红色,细颗粒较多,黏性较大。试验所用的土料物理指标见表1,土料的颗粒分析曲线见图1。
1.2 玄武岩纤维
本试验所取用6 mm玄武岩纤维,掺入时需将纤维丝均匀掺加。玄武岩纤维性能参数[14]见表2。
1.3 试样制备
选取代表性土样,测定含水率,并按照目标含水率计算出所需加水量;在配完目标含水率之后,将目标含水率土料装入塑料袋中并置于密闭的玻璃缸中养护至少20 h,实际测量值与理论值的差值好的目标含水率土料根据干密度要求称取并与玄武岩纤维掺合。加入玄武岩纤维时,由于有些玄武岩纤维呈絮凝状,所以在加入玄武岩纤维拌合前,要对玄武岩纤维进行处理,使其能够在土料当中分散均匀为宜。将纤维丝均匀地分散在土料中,拌和均匀。并将拌和后的土料平均分成五份,逐层击实,击实前先进行振捣使土颗粒均匀分布,每层击实完成后,为了使两层土之间能够更好的粘结在一起,刮毛接触面,再倒入下一层土料,直至第五层击实完毕后,不再进行刮毛处理,取下护筒。最后将击实好的试样取出,称其质量,每个试样的密度差值应小于0.02 g/cm3。

表1 试验所用土料的物理指标
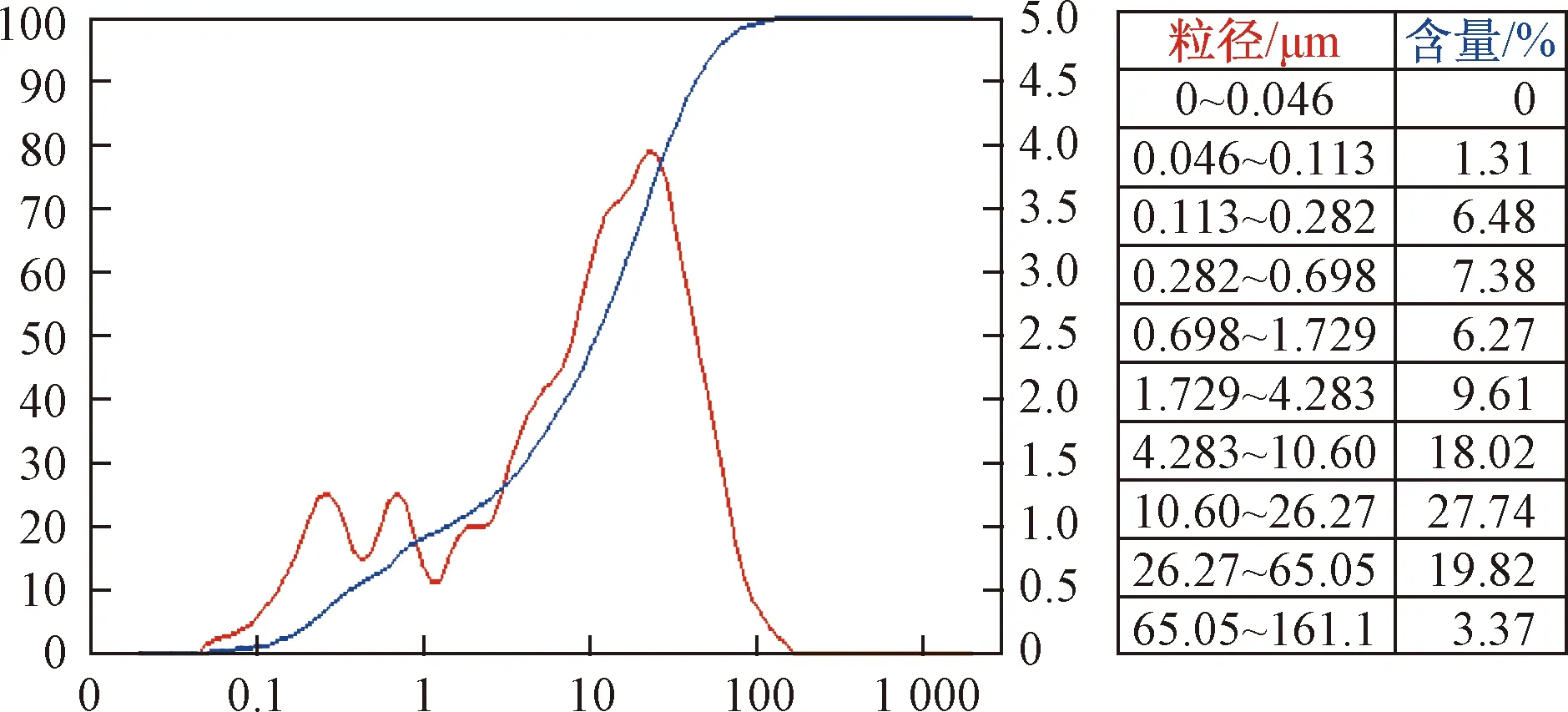
图1 黄土的颗粒分析曲线Fig.1 Gradation curve of loess

表2 玄武岩纤维性能参数
1.4 试验方案
正交试验是科学研究中经常采用的一种试验安排方法。如果巧妙地利用正交设计试验,弥补在安排试验时出现多种因素且无法用控制变量法进行的不足,可以达到事半功倍的效果[15]。
拟选择可能对抗剪强度有较大影响的三个因素作为指标,每个指标确定四个水平等级。即根据土料含水率(A)水平为11%(1)、13%(2)、15%(3)、17%(4),压实度(B)水平为0.85(1)、0.90(2)、0.93(3)、0.95(4)以及玄武岩纤维掺量(C)水平为0.0%(1)、0.2%(2)、0.4%(3)、0.6%(4)完成三因素四水平正交设计并安排16组试验(例如,B2表示压实度为0.90)。三因素四水平正交表L16(34)见表3。再对正交试验得出的结果进行优化,安排不同围压不同围压(50 kPa、75 kPa、100 kPa)、不同纤维掺量(0.0%、0.2%、0.4%、0.6%、0.8%)下同等试验。
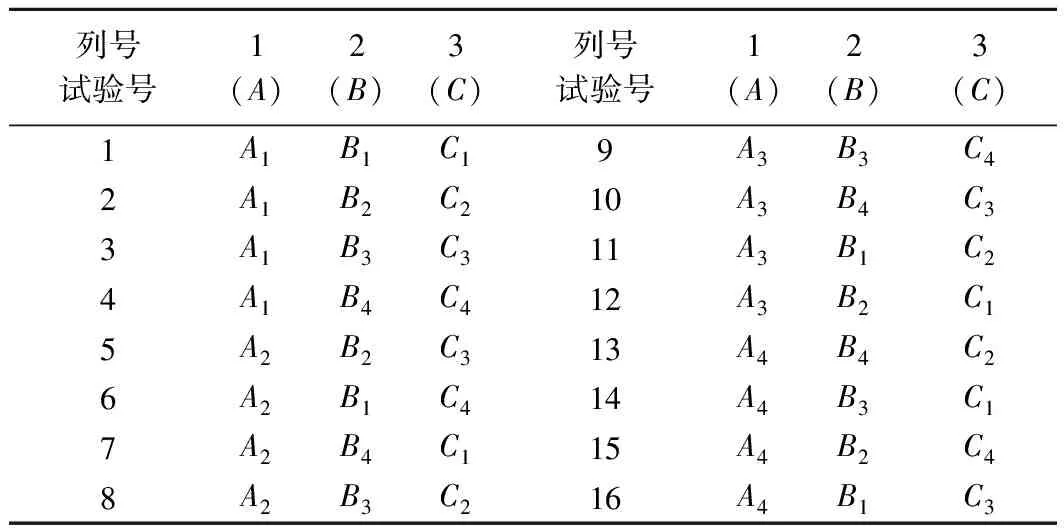
表3 三因素四水平正交表L16(34)
2 正交试验结果
2.1 试验结果
通过极差分析可知,A1B4C3为三轴试验玄武岩纤维土的抗剪强度指标的最优参数方案。此时,对应于因素的水平为含水率11%、压实度0.95、玄武岩纤维掺量0.4%。因子的主次顺序为A→B→C,简记为ABC。
对方差进行了分析可得,各因素的试验误差大小关系为:压实度>纤维掺量>含水率;显著性检验结果影响大小顺序为:含水率影响>压实度影响>玄武岩纤维掺量影响。
查表知,F0.99(3,6)=9.78,F0.95(3,6)=4.76,F0.90(3,6)=3.29。对比表4中F值的大小可知显著因子为含水率、压实度和玄武岩纤维掺量。其中含水率和压实度影响极显著,而纤维掺量影响为显著。其中,Ti为各因素同一水平试验指标之和。R*为最小误差列的判定指标。DF为平均偏差平方和。
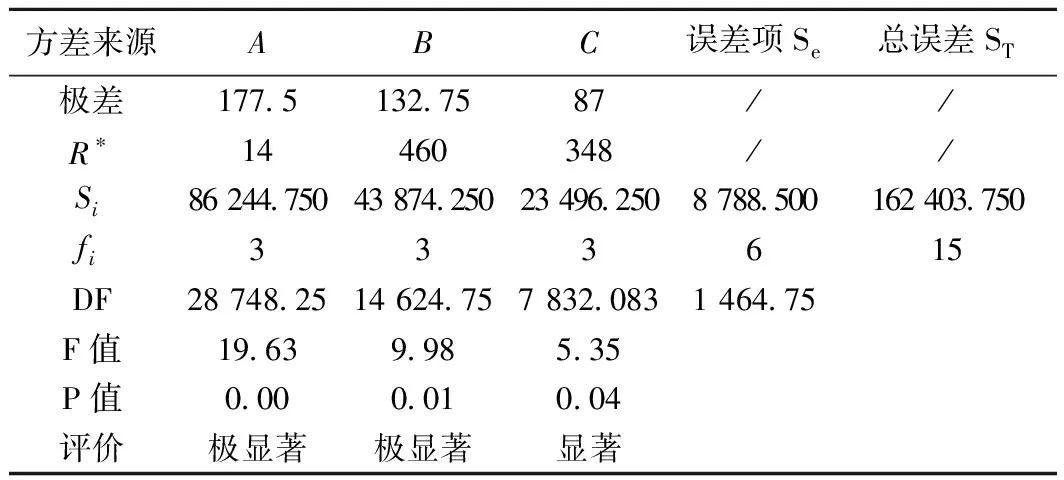
表4 玄武岩纤维土抗剪强度的极差、方差及影响分析
虽然正交试验设计所得到的16组试验数据并没有直接进行比较的基础,但能通过直观分析法和方差分析法两种方法分析得出最优配合比A1B4C3,即:含水率为11%、压实度为0.95、玄武岩纤维掺量为0.4%。
2.2 应力-应变曲线
玄武岩纤维加筋黄土的应力-应变曲线如图2所示。正交设计下的试验组合两两之间没有直接比较的基础,在控制含水率一定的情况下可以分别对比分析纤维掺量和压实度的影响。
(1)图2(a)中,在含水率为11%时,随着纤维掺量的增加,应力-应变曲线由弱硬化型向弱化型转变,强度最高时纤维掺量为0.6%,其次是纤维掺量为0.4%,0.2%和0.0%,且在0.6%、0.4%、0.2%的纤维掺量下应力-应变曲线表现为软化型,其原因是,纤维与土颗粒粘结在一起,在试样被剪切的过程中,纤维随之产生拉应力,拉应力在一定程度上抑制了试样破坏的趋势,即表现为试样的剪切强度增加。图2(b)中,在含水率为13%时,由于压实度达到最大,此组曲线在0.0%的纤维掺量下强度可以达到最高,但表现为软化型,在达到峰值前基本成直线,达到峰值后强度突然下降,而其他三条曲线加入了不同掺量的玄武岩纤维,破坏呈现软化型,其原因在于纤维的加入能够有效提高土体的韧性,而使破坏形态表现为塑性。图2(c)中,强度最高时的纤维掺量为0.4%,四组曲线均呈现弱软化型向硬化型发展的趋势,其原因是含水率的升高使得土颗粒晶层间的水分子增多,双电层厚度逐渐变厚,土颗粒相互远离重新排列,而出现应变-硬化的塑性破坏曲线。
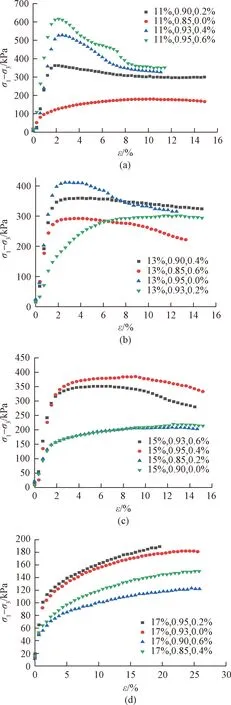
图2 不同含水率条件下的应力-应变曲线Fig.2 Stress-strain curves with different moisture contents
(2)如图2中含水率一定时,最大抗剪强度的压实度都为0.95。通过比较分析(a)、(c)发现抗剪强度随压实度升高而增大,原因是压实度越大,土颗粒间孔隙越小,土颗粒间土颗粒相互错动并重新排列,由于纤维和土颗粒间的握裹作用和纤维网作用使得抗剪强度增大;分析(b)、(d)可知,由于纤维掺量的不同,与(a)、(c)规律稍有差异,但分析结果相一致,对(b)、(d)中抗剪强度受纤维掺量和压实度的影响进行分析,纤维掺量虽都不是最大掺量,但所对应的压实度为最佳值;而(a)、(c)中,压实度不是最大值,但其最大纤维掺量发挥其与土的界面作用而取得同条件下最优。
3 最优配合比优化分析和评价
以上通过正交试验结果得出的最优配合比,也就是从最大限度提高三轴试样的峰值强度,但未必是最经济的,而直观分析法中纤维掺量为相对次要因素,控制含水率和压实度分别满足最优配合比(11%、0.95)的前提下,考虑到围压和玄武岩纤维掺量对试验结果的影响,故将玄武岩纤维掺量(0.0%、0.2%、0.4%、0.6%、08%)及围压(50 kPa、75 kPa、100 kPa)作为影响因素对最优配合比进行试验,获得抗剪强度随围压增长的规律,通过绘制摩尔强度包线,得到抗剪强度指标。
3.1 不同围压、不同纤维掺量下的三轴试验
含水率为11%、压实度0.95的条件下进行不同围压、不同纤维掺量下的三轴试验,所得到的试样破坏情况均为鼓胀型破坏(图3)。得出的不同围压、不同纤维掺量下的抗剪强度(图4)。

图3 试样破坏形态图Fig.3 Damage pattern of the sample
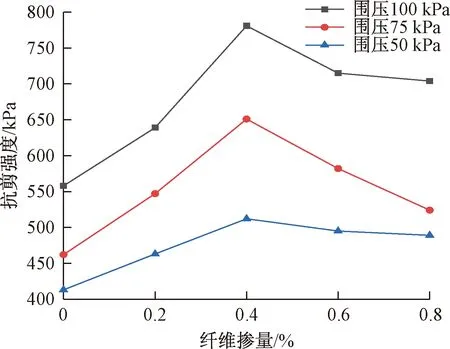
图4 不同围压、不同纤维掺量下的抗剪强度曲线Fig.4 Shear strength curves under different confining pressure and different fiber content
从图4中可以看出,同一围压下的最佳纤维掺量为0.4%,与正交试验经过方差分析得出的结论一致。土体是摩擦型材料,通过对最优配合比作进一步试验得出抗剪强度随围压的增大而增大,试样的抗剪强度随玄武岩纤维掺量的增加先增大后减小。
3.2 不同纤维掺量试样的内摩擦角和黏聚力的计算及分析
在不同围压下进行剪切破坏时得到的最大轴向应力σ1,则试样的大主应力为σ1,而小主应力为围压σ3,在坐标轴上以(σ1-σ3)为直径,(σ1+σ3)/2为圆心画极限应力圆。应用Excel规划求解功能三轴试验抗剪强度指标绘出的抗剪强度包络线。计算结果见表5。
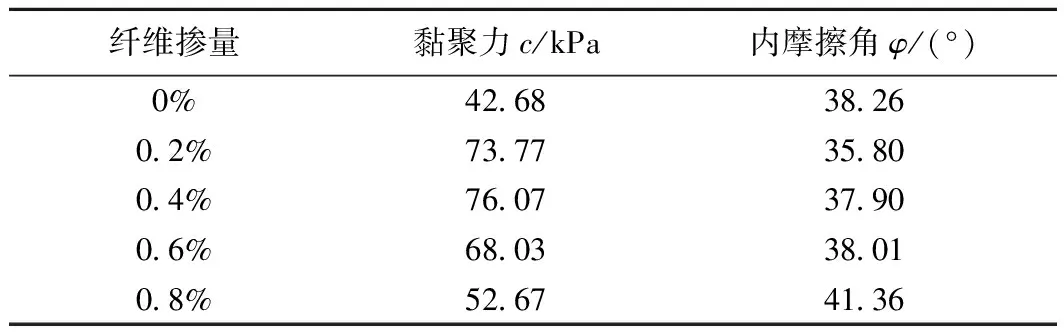
表5 不同纤维掺量下土的黏聚力c和内摩擦角φ
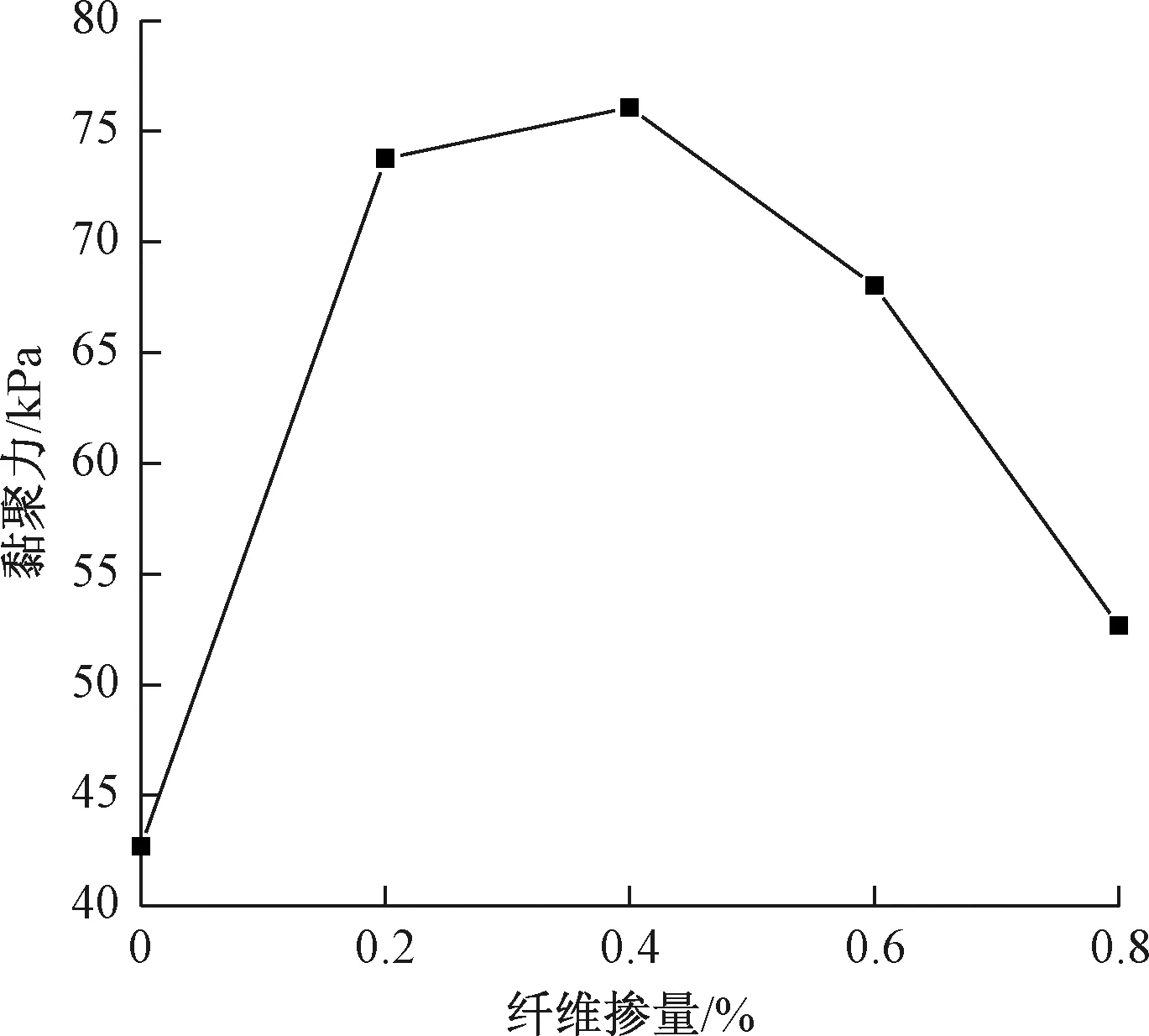
图5 黏聚力Fig.5 Cohesion
通过绘制黏聚力随纤维掺量的变化曲线(图5),发现玄武岩纤维的添加能够有效提高土样的黏聚力,并且土样的黏聚力先随纤维掺量的增加先增大后减小,当纤维掺量在0.4%左右时,黏聚力最大。绘制内摩擦角随纤维掺量的变化曲线可以看出(图6),纤维掺量为0.2%时,内摩擦角明显减小;纤维掺量为0.8%时,内摩擦角发生了较为显著的升高;其余的相差都不大,由图6可以看出,纤维的掺入对土样的内摩擦角影响曲线呈上凹形状,实际工程中应控制纤维掺量不少于0.2%。
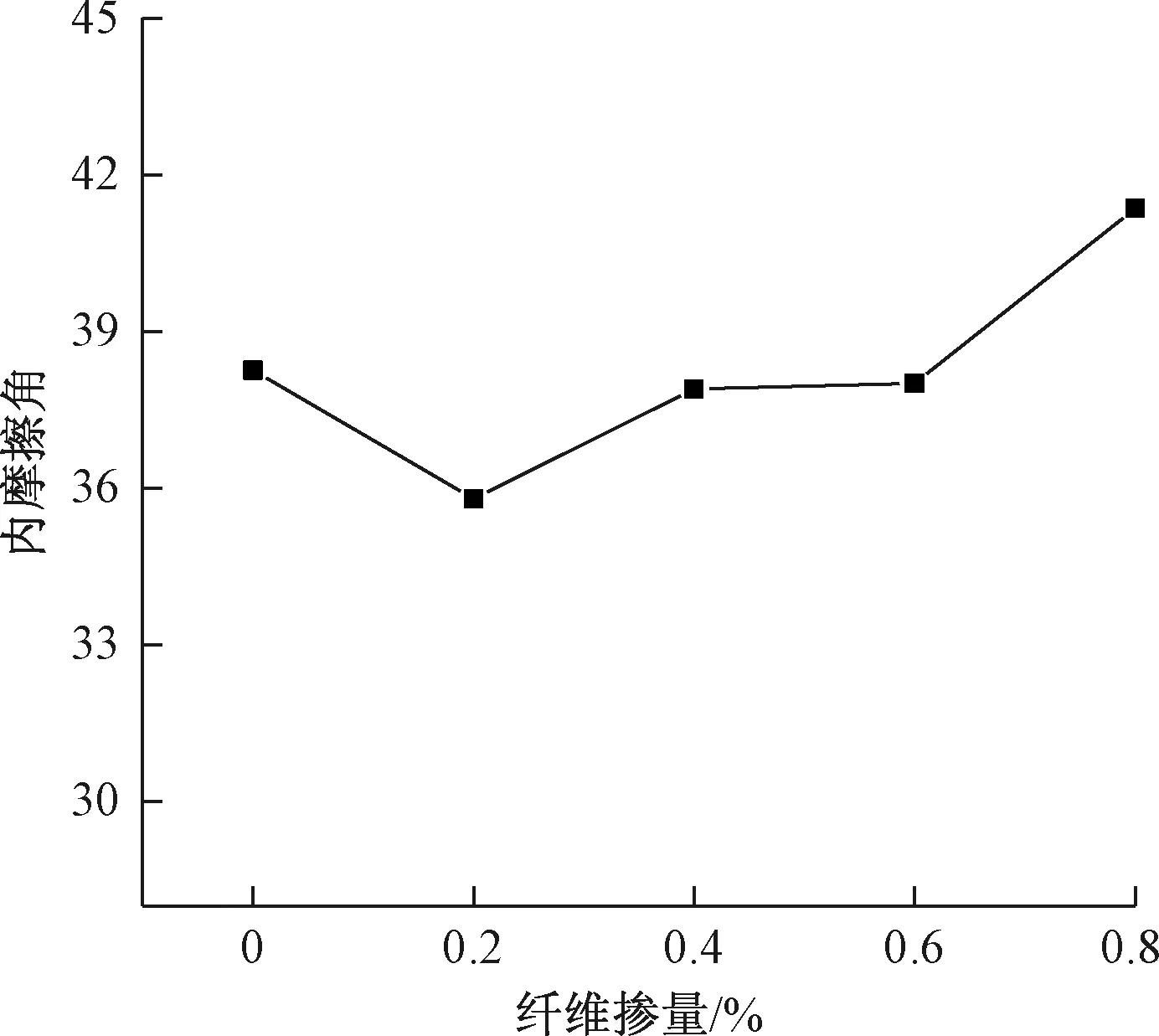
图6 内摩擦角Fig.6 Internal friction angle
4 结论
(1)方差分析得到的最优配合比为含水率11%,压实度0.95,玄武岩纤维掺量0.4%。
(2)通过对最优配合比作进一步研究,在压实度和含水率保持不变的情况下,玄武岩纤维加筋黄土的抗剪强度随围压的增大而增大,随玄武岩纤维掺量的增加先增大后减小。
(3)含水率、压实度、玄武岩纤维掺量、围压都是抗剪强度的显著影响因子。玄武岩纤维的添加能够有效提高土样的黏聚力,并且土样的黏聚力随纤维掺量的增加先增大后减小,当纤维掺量在0.4%左右时,黏聚力最大。纤维掺量为0.2%时,内摩擦角明显减小,纤维掺量为0.8%时,内摩擦角发生了较为显著的升高;其余的相差都不大,内摩擦角和掺量所呈曲线为上凹形,实际工程中应将纤维添加均匀,控制纤维掺量不少于0.2%。
