矿柱稳定性判别的ICA-RoF模型及其工程应用

肖屈日，赵国彦，刘 建，简 筝

(1.中南大学资源与安全工程学院，湖南 长沙 410083；2.长沙矿山研究院有限责任公司，湖南 长沙 410012)

0 引言

在地下采矿工程中，为了安全和便利通常会有意保留部分矿体作为支柱，矿柱的合理留设不仅有支撑顶板的作用，还能有效地保护巷道和地面建筑物[1]。随着采掘工作推进、开采向深部延伸，顶板暴露面积慢慢变大、矿柱应力逐渐增加，矿柱失稳的风险也愈发严峻。作为影响采空区稳定的关键结构单元[2]，矿柱失稳可能会导致柱体不同程度的自由面岩石剥落、剪切破坏、内部劈裂和地质结构面的滑移与溃曲破坏[3]，更甚者将引发冒顶和空区塌陷事故[4]，给矿山企业(特别是房柱法开采[5]矿山企业)人员和财产安全造成巨大的威胁。因此，开展关于矿柱稳定性的研究对于地下矿山高效开采、灾害防治具有重要现实意义。

国内外学者针对矿柱的设计与稳定分析问题提出了许多理论方法，如：面积承载理论[6-7]、经验公式法[7-8]、数值模拟技术[4-5,9]等。传统的矿柱稳定性分析方法主要根据这些理论与手段得到矿柱强度、应力等数据，以矿柱强度与应力之比来衡量矿柱的安全性。尽管这些方法已经发展的十分成熟，但导致矿柱失稳的因素众多，单一经验指标评判存在可靠性低、判别效果差的问题。机器学习方法以多特征指标为输入，将比较评判过程无形纳入学习算法的“黑匣子”中，并借助大量的实例数据进行监督学习，使得分析更为可靠和高效，近年来被广泛应用于矿柱设计和稳定性评估中[10-12]。本质上，同经验公式法一样，机器学习算法也是一种基于数据的统计方法，但机器学习算法能够借助计算机的高速计算能力总结出人类暂时无法归纳出的“经验”。通过机器学习算法逆构矿柱稳定性影响因素与矿柱状态之间的非线性映射关系来判定未知矿柱的稳定性，对指导工程实践有着积极而深刻的作用。

旋转森林算法是由JUAN J RODRIGUEZ等[13]于2006年提出的新型集成学习算法。与随机森林等经典集成学习算法相比，旋转森林算法能够生成差异度大且精度较高的基分类器，具有更好的泛化能力，近年来被广泛应用于生物医学[14-15]和模式识别[16]等诸多领域。目前，尚未有关旋转森林算法在矿柱稳定分析方面的应用研究。因此，本文在概述旋转森林相关理论研究的基础上，将其引入到矿柱稳定性分析中，构建出一种基于ICA-RoF算法的硬岩矿柱稳定性判别模型，以期为地下矿山的矿柱设计与安全评价工作提供参考。

1 ICA-RoF理论与算法

1.1 旋转森林算法

旋转森林算法[13]通过对原始样本特征进行处理，并采用一定的特征变换方法获取训练基分类器所需的不同样本集，以实现基分类器个体间的差异性，从而达到提高分类准确率的目的，其算法流程如图1所示。首先，定义训练数据集D={X,Y}={(x1,y1), (x2,y2),…,(xn,yn)}，其中：xi∈RP是训练集的输入；yi∈{C1, C2,…, Cm}是训练集的输出；F为训练集D的特征集。其次，旋转森林算法需要预先给定参数：子集特征数s和集成规模L，它们分别代表每一个特征子集所包含的特征指标个数和集成系统所包含的基分类器个数。整个算法共分成基分类器生成与基分类器合成两个阶段。

图1 旋转森林算法流程图Fig.1 Procedure of rotation forest

(1)基分类器生成阶段

①将原始特征集F进行随机分割，每个子集包含s个特征指标，任意两个子集间互不相交，无法整除者，将余数部分归为一个子集，共得到k个子集，第i个基分类器的第j个特征子集记为Fij。

②从数据集X提取Fij全部样本，采用bootstrap方法随机抽取75%样本生成样本子集Xij。

③按照特征变换算法计算Xij的变换矩阵Wij。

④将变换矩阵Wi1,Wi2,…,Wik按照式(1)排列构造稀疏矩阵Wi。

(1)

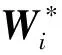
(2)基分类器合成阶段

2）钻孔冲洗。灌浆前，要进行钻孔孔壁冲洗和裂隙冲洗，冲洗过程中同步进行抬动观测。钻孔冲洗后，孔内残存的沉积物厚度不得超过20cm，需进行钻孔电视（钻孔全景成像）的钻孔需达到孔内水清净。

⑧利用基分类器Gi对x′i进行预测，得到分属C1, C2,…, Cm的概率P1(x′i),P2(x′i),…,Pm(x′i)。

⑨重复步骤7～8，得到全部基分类器的分类结果，按照式(2)对分类结果进行集成。

(2)

⑩将样本x划分到概率最大的类别中，得到最终的集成分类结果。

1.2 特征变换算法

决策树是敏感分类器，数据的任何微小改变都可能使训练得到的决策树构造完全不同[14]。因此，特征变换方法对于构造有差异的数据分量起着至关重要的作用，并直接影响最终的分类结果。常用的特征变换方法包括主成分分析(PCA)、非参数线性判别(NDA)、稀疏随机映射(SR)和随机映射(R)等，大量数据实验结果表明：基于PCA特征变换的旋转森林算法(PCA-RoF)性能最好[17]。

独立成分分析(ICA)是基于高阶统计量的多特征数据处理方法，它将数据集特征转换为若干个统计独立的特征组合，从而保证数据集的高阶统计特性。ICA被视为PCA的一种重要扩展，同样适合作为旋转森林的特征变化方法，且与其它特征变换算法相比，ICA具有以下优势：提供更符合实际的统计模型，可以更好地确定数据在高维空间的位置； 提供了一种非正交基空间，当原始数据集存在离群点时，能够更好地对数据信息进行重建；对高阶统计信息比较敏感，而PCA只对二阶信息敏感。目前，ICA的估计算法主要有4种：FastICA、InfoMax、JADE、Radical-ICA[18]。

2 工程实例

2.1 确定特征指标

关于矿柱的稳定性问题，国内外学者有一个普遍共识，即矿柱对采矿所引起荷载的整体响应取决于矿柱的形状特征、矿柱岩体的地质构造和围岩对矿柱所施加的表面约束特性。当围岩所施加的约束大于矿柱该形状特征下岩体构造所能承受的极限时，矿柱就会发生破坏[19]。因此，矿柱稳定性研究可总结为如图2所示的评价体系：矿柱的稳定性分析主要分为宏观的强度评价和微观的应力评价两种途径，理论上来说宏观强度与微观应力存在着关于岩质构造、形状特征的一一对应关系，但由于岩体非均质且构造受多种因素影响，并无有效的度量方法。因此，在寻找其对应关系的问题上存在无法攻克的难点，从而催生出一系列逼近关系的研究方法。表1整理了近年部分文献的指标选取情况，所有研究方法的考量因素均包含形状特征量、力学状态量和力学极限量三类，三者缺一不可。

(3)

图2 矿柱稳定性评价体系Fig.2 Framework of pillar stability evaluation

表1 相关文献的指标选取情况

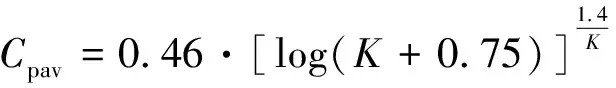
(4)

PS=0.44·UCS·(0.68+0.52κ)

(5)

其中，κ为矿柱摩擦系数，计算公式为：

(6)

为更全面反应矿柱稳定情况、提高识别准确率，本文除选取4个直接指标外，同时将矿柱高宽比K、矿柱约束Cpav、矿柱摩擦系数κ以及矿柱强度PS纳入数据库的指标考量范围。尽管衍生指标不是直接来源于实际工程，矿柱应力δP也非基于同一方法得出，但更多特征输入能够给予模型必要的信息余度和特征选择的可能性。最重要的是上述指标根据统计经验得出，是Per John Lunder[7]大量工作的经验成果，经过许多研究方法所检验，其结果能够较为准确地反映矿柱的实际状况(图3)。

2.2 数据采集与处理

模型所需基础数据取自文献[7](共含有178例样本)，剔除掉16例直接指标缺失样本，得到一个含有162个完整硬岩矿柱样本的数据库。关于矿柱稳定性的分级标准，各组织和学者观点不尽相同，其范围从简单的“稳定/破坏”两级标准到五级或六级的更精细化标准。为实现分类标准的简单实用功能和模型对新样本数据的兼容性，本文选取最简单的“稳定/破坏”两级分类作为模型的分级标准，同时考虑到不稳定矿柱的破坏渐进特性，将文献[7]中通用分级方法的不稳定矿柱和破坏矿柱合归为同一类，稳定矿柱依然独成一类，分别采用“F”和“S”标记矿柱的破坏和稳定状态。图3为所建数据库8类特征指标的箱线图。

2.3 模型检验及应用实例分析

模型输入量为(W,H,δP,UCS,K,Cpav,κ,PS)，输出为“稳定/破坏”两级类别V：“F”和“S”，输入输出间存在ICA-RoF算法的映射关系F(W,H,δP,UCS,K,Cpav,κ,PS)→V，具体检验过程如图4所示。

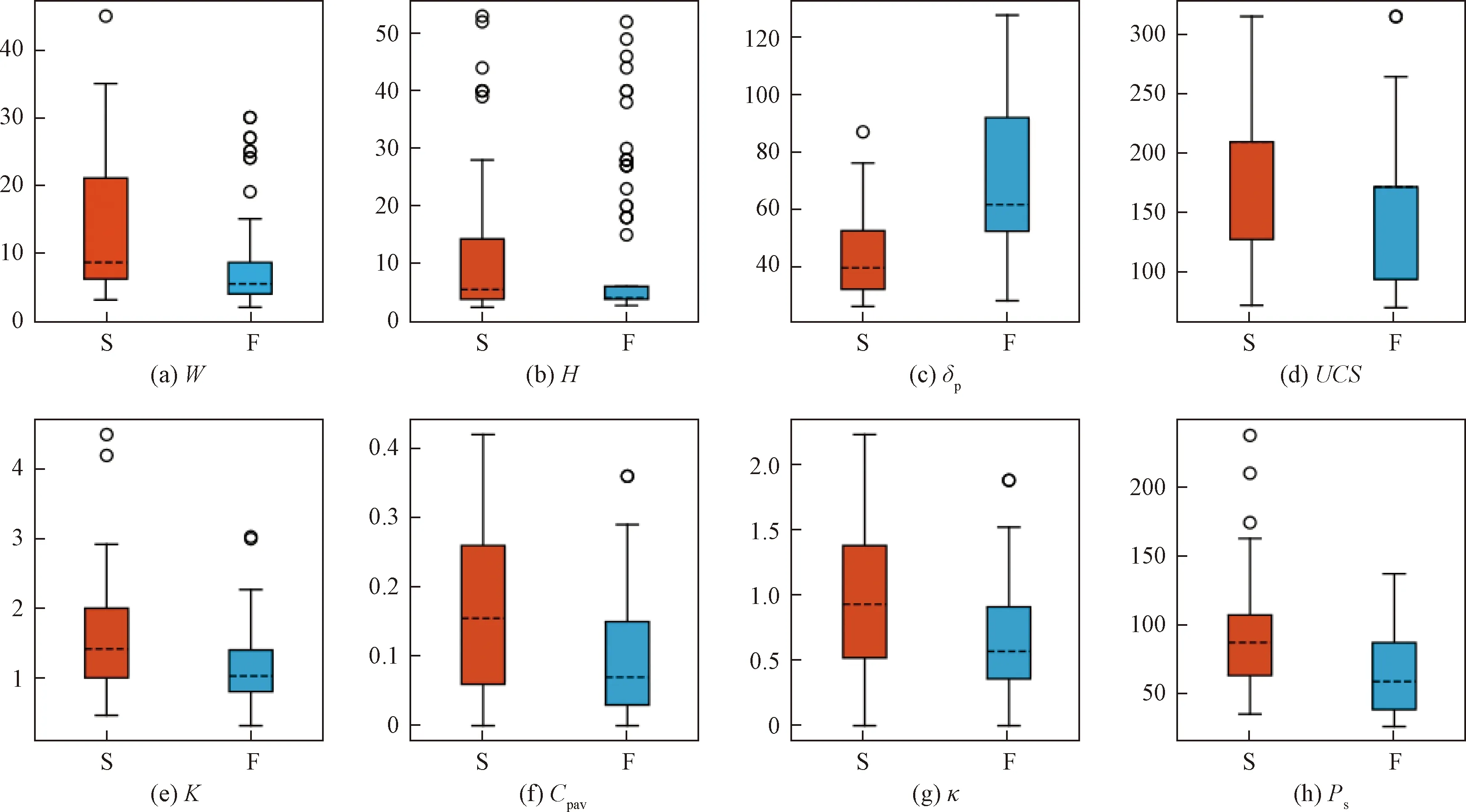
图3 矿柱样本特征箱线图Fig.3 Boxplots of pillar sample data

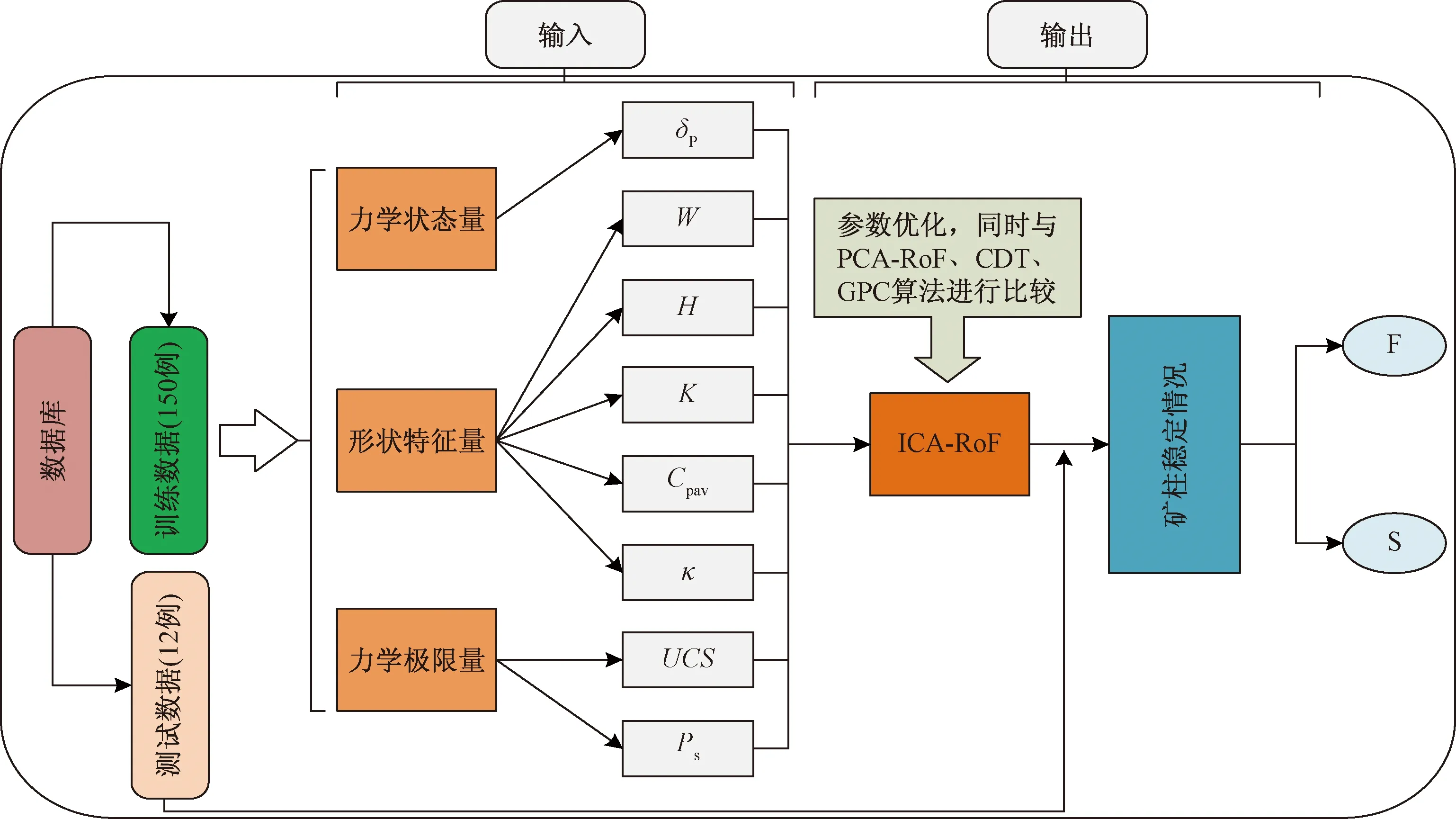
图4 矿柱稳定性判别的ICA-RoF模型及其检验过程Fig.4 The ICA-RoF model of pillar stability recognition and its testing procedure

模型的构建与检验均在Python2.7环境下进行，相关程序通过调用NumPy、SciPy和sklearn等库进行编写，且在同一平台上运行，具体的电脑配置为：操作系统：Windows 7旗舰版64位；CPU：Intel(R) Core(TM) i3-4160 3.60 GHz；RAM：4.00 GB。基分类器和特征变换方法均直接引用于sklearn库。其中，基分类器采用CART决策树(CDT)，按信息增益划分节点数据集，为防止模型过拟合，将节点最少样本数量限制为3%(min_samples_split=0.03)，其余采用默认设置；ICA特征变换矩阵基于FastICA函数获得，其参数设置为：algorithm='parallel'，whiten=True，max_iter=200，tol=0.000 1。

为获得可靠的ICA-RoF算法映射F→V，用5折交叉验证方法对训练集数据进行遍历寻优计算，并根据40次运行结果的平均识别准确率选取ICA-RoF算法的最优参数，运行结果如图5所示。寻优过程同时对比PCA-RoF算法，可以明显看到：随着集成规模的增加，两种算法的平均准确率不断提高，且在集成规模达到10后逐渐趋于稳定；当子集特征数为4时，两种算法均获得最高的识别准确率。两种基于不同特征变换矩阵的旋转森林算法的规律不尽相同，但ICA-RoF算法的平均准确率高于PCA-RoF算法，且这一结果不因集成规模和子集特征数大小而改变。考虑到计算时间与集成规模成正比，故选取L=10、s=4作为模型性能和计算消耗的折中优选参数。

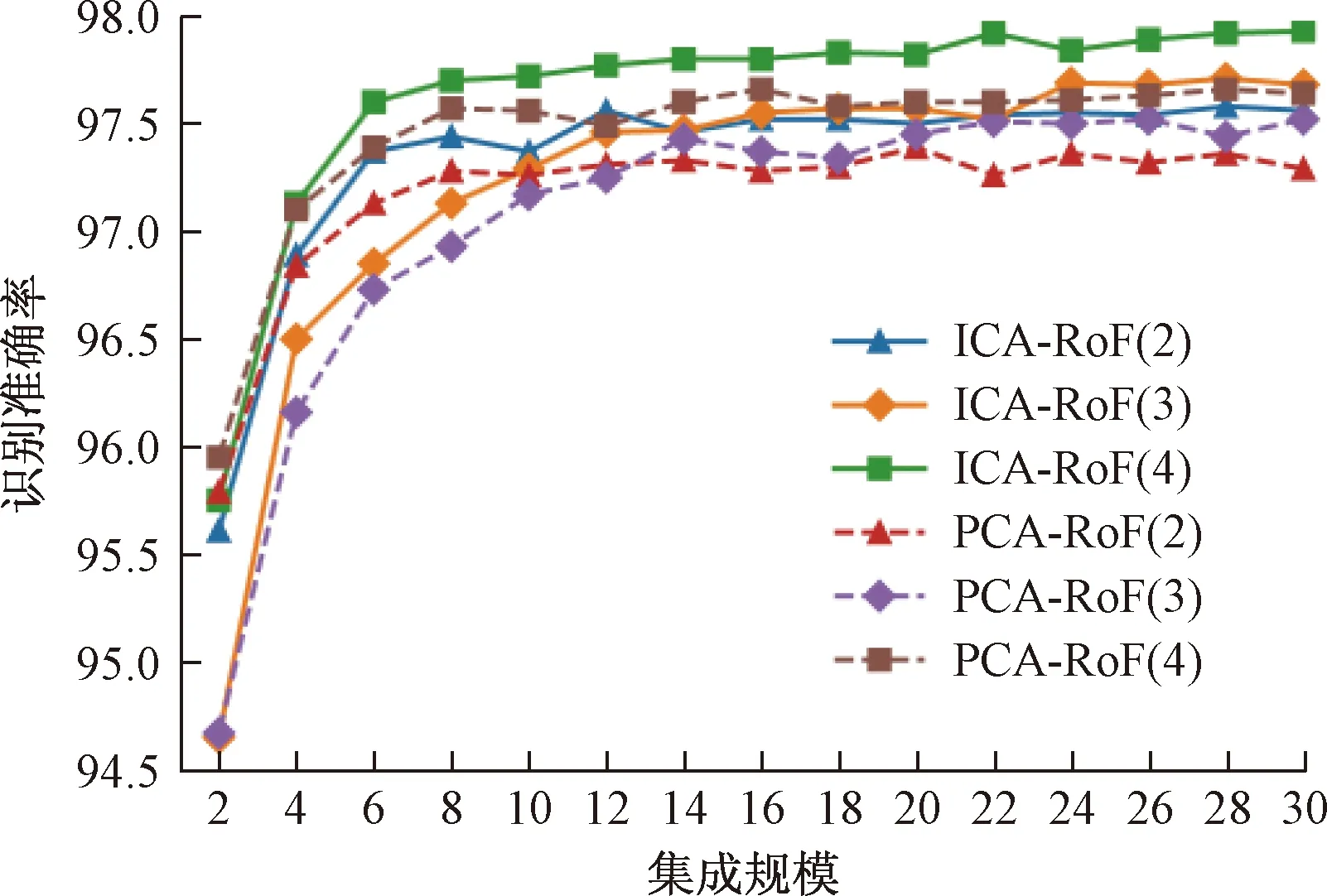
图5 参数寻优运行结果Fig.5 Results of searching parameter

当L=10、s=4时，训练集数据200(50×4)次运行结果的准确率统计特性如表2所示。为客观反映算法性能、科学检验模型效果，本文同时选择PCA-RoF算法、CDT(基分类器)算法和文献[23]中所述性能最为优越的GPC算法进行了相同条件下的对比研究，结果见表2。对各算法准确率总体的均值之差进行统计学检验(独立大样本的Z检验)，经检验可认为：在显著性水平α=0.05的情况下，ICA-RoF算法的平均准确率明显高于其余3种算法。

同时，根据上文所构建的4种模型对12组测试集数据进行判别，判别结果见表2。从表中的识别结果可知：除了CDT算法的识别准确率仅为83.33%(10/12)外，ICA-RoF算法和其余两种算法识别结果一致，仅有1个误分类，准确率达91.66%，与实际吻合情况较好，从而说明ICA-RoF硬岩矿柱破坏识别模型同样具有较强的泛化能力。

与其它模型相比，基于ICA-RoF算法的矿柱稳定性判别模型具有如下优点：①数据处理简单，对新数据的兼容性好，有利于数据库的拓展；② 识别准确率高，泛化能力好，算法映射更为可靠；③决策树作为基分类器，可以处理连续变量和类型变量，受异常值影响小。同时，该模型也存在着不可避免的缺点：①算法复杂度大，将耗费更多的计算资源与时间；②对于不平衡数据集，ICA-RoF算法的识别结果将更倾向于数量更多的类别。总体来说，使用ICA-RoF算法来识别硬岩矿柱的破坏情况，是完全可行且可靠的，无论对于前期的采矿工程设计，还是后期的工程灾害防治，都有其实际意义。更广泛的收集矿柱稳定性数据，建立更详细的数据库，开发大数据平台，将使该模型的可靠度更高。

表2 不同算法的性能比较

3 结论

(1)通过分析矿柱破坏机理，总结归纳矿柱稳定性研究的一般方法体系，明确矿柱稳定性判别模型应包含形状特征量、力学状态量和力学极限量3方面指标。三者相互联系，缺一不可。

(2)矿柱稳定性级别采用最简单的“稳定/破坏”两级分类标准。该分类标准简单实用，对新样本数据的兼容性好，有利于对数据库进行拓展。

(3)通过对所建模型进行网格式参数寻优计算，发现：矿柱识别准确率会随着ICA-RoF的集成规模的增加而增大，当集成规模达到10后逐渐趋于稳定；当子集特征数为4时，模型整体识别率最高。

(4)通过模型对比实验可知：ICA-RoF识别模型的识别精度高、泛化能力好，其平均准确率显著高于PCA-RoF算法、CDT算法和GPC算法(α=0.05)。