钢水“脱氧合金化”配料方案的优化

刘芳宇，周毅，唐佳鑫，简思源

（1.南华大学计算机学院，衡阳421000；2.南华大学资源环境与安全工程学院，衡阳421000；3.湖南中医药大学医学院，长沙410000；4.怀化学院化学与材料工程学院，怀化418000）

0 引言

（1）问题背景

自铁矿石长协机制被打破，铁矿石价格居高不下，我国钢铁业已然进入薄利期。在保证钢水高质量的同时最大限度地降低合金钢的生产成本，成为了钢铁企业获得市场竞争力的关键。因此，建立脱氧合金化模型，在线预测并优化投入合金的种类和数量的研究工作显得尤为重要。

从上世纪80 年代至今，人们对于这个课题进行了多角度、多方面的研究。1960 年，Richard H R 等人[1]研究了Si 在CaO+SiO2渣系和CaO+SiO2+Al2O3渣系内发生的不同反应，以及不同温度下合金元素在渣系内发生的化学反应，为之后的合金化模型的研究奠定了理论基础。2001 年，李延辉等人[2]提出一种基于神经网络的智能LF 控制系统模型，该模型的核心是脱氧合金化过程钢水成分的实时预测。2005 年，米卫等[3]以钢水、渣、包衬为研究体系，建立了钢水成分与温度控制模型，在补加系数法的基础上考虑了合金收得率，推出了合金添加公式和钢水成分预报公式。

（2）问题叙述

在问题背景的基础上，本文将依据《炼钢历史数据》和《常用合金料成分说明》建立模型，这两份数据来自于：http://www.mathorcup.org/detail/2273，为了实现钢水“脱氧合金化”方案的优化。我们需要讨论以下几个问题：

①根据《炼钢历史数据》计算C、Mn 两种元素的历史收得率，并分析影响其收得率的主要因素。

②在①的基础上，对C、Mn 两种元素的收得率进行预测，并进一步改进算法，提高这两种元素的预测准确率。

③根据②合金收得率的预测结果及《常用合金料成分说明》，实现钢水脱氧合金化成本优化计算，并给出合金配料方案。

1 符号说明

表1

2 问题的分析与求解

2.1 问题1的分析与求解

（1）C、Mn 两种元素历史收得率的计算

元素的收得率是指脱氧合金化时被钢水吸收的元素

fi-元素i 的收得率；

Gxi-元素i 被钢水吸收的重量；Gji-元素i 加入的总重量。

合金元素的加入量取决于加入合金配料的重量及配料中各元素的比重，则合金元素加入量公式如下：

gn-配料中n 合金料的重量；

cin-n 合金中i 元素占的比重。

已知《炼钢历史数据》中各元素的转炉终点和连铸正样，在不考虑电极增碳的情况下，计算得出的C 元素的历史收得率有将近25%大于100%，同样地，在不考虑钢水回锰的情况下，计算得Mn 元素的历史收得率大都大于100%，这与常理相悖。

参考胡井涛等人[4]在LF 精炼的研究，本文采用下列式子来求解钢水中合金元素的吸收量：

ωzi-脱氧合金化之后元素i 的质量分数；

ωci-脱氧合金化之前元素i 的质量分数；

Δωi-元素i 的其他来源，如碳的电极增碳量，锰的钢水回锰量等。

当考虑碳的电极增碳量时：t- 指时间，本文默认为1 小时；G-钢水的重量（单位：吨）当考虑锰的钢水回锰量时：

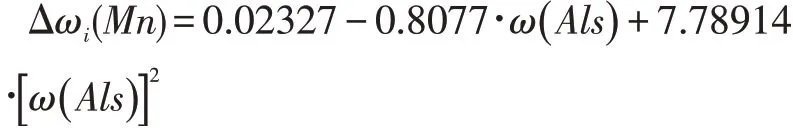
ω( Als) -( Als )的连铸正样，单位为%；

通过上列各式计算出碳、锰两种元素的历史收得率，并对求得的收得率作分布图，如图1 和图2 所示。

显然，在考虑电极增碳和钢水回锰的情况下，C 元素的收得率普遍在0.65-0.85 区间内，Mn 元素的历史收得率普遍在0.85-1.03 区间内。

图1 碳元素的历史收得率

图2 锰元素的历史收得率

（2）影响C、Mn 两种元素收得率主要因素的分析

为分析C、Mn 两种元素收得率的主要影响因素，本文将二者的历史收得率分别与转炉终点温度、加入的16 种合金配料量、钢水净重、转炉终点元素量等进行Pearson 相关性系数分析，找出影响历史收得率的主要影响因素，分析式如下：

通过上式计算出C、Mn 两种元素历史收得率与各类因素的相关性数据，并从中提取出相关性较为显著的几类因素，相关性表格如表2。

表2 C、Mn 元素历史收得率的相关性表

由表2 可知，除了前文考虑的电极增碳以外，影响C 元素收得率的因素主要为钢水净重（高达0.585）以及转炉终点C、Mn、S、P 等元素重量百分比，影响Mn 元素收得率的因素主要为钢水净重（高达0.891）以及转炉终点C、Mn、S、P、Si 等元素重量百分比。

2.2 问题2的分析与求解

本文拟采用多元线性回归方法进行分析，预测C和Mn 两种元素的收得率。

（1）对C 元素收得率预测模型的建立与求解

通过分析，影响C 元素历史收得率最主要的三个因素为：钢水净重、转炉终点C、Mn 元素重量百分比，假设C 元素收得率的拟合公式为：

通过SPSS 软件进行多元线性回归分析，可以得到C 元素的回归标准化残差的直方图(图3)和回归标准化的正态图（图4）。

图3 碳元素收得率的回归标准残差直方图

图3 中正态曲线也被显示在直方图上，用以判断标准化残差是否呈正态分布。大致判断其呈正态分布。

图4 碳元素收得率的回归标准化正态图

图4 给出了观测值的残差分布与假设正态分布的比较，由该图可知标准化残差散点分布靠近直线，可判断C 元素收得率的标准化残差成正态分布。

由图3、图4 可以发现拟合的结果较接近实际值，通过线性回归得到表3。

表3 碳元素收得率预测值的回归系数表

每个影响因素的显著性小于0.1，则可以认为其具有显著性意义，故得到C 元素收得率的预测方程：

对该方程进行数值验算，代入五组数据进行求解得到其相对误差表如表4。

表4 碳元素收得率预测方程的相对误差表（线性回归）

可以发现预测相对误差在6.25%以内，预测相对较精准，故该预测方程合理。

（2）对Mn 元素收得率预测模型的建立与求解

影响Mn 元素的历史收得率的因素有：钢水净重、钢水中C、S、Mn、Si 在脱氧合金化之前的质量等五个因素，对Mn 元素进行多元回归分析，假设其方程为：

同理，采用SPSS 软件进行多元线性回归分析，可以得到Mn 元素的回归标准化残差的直方图（图5）和回归标准化的正态图（图6）。

由图5、图6，Mn 元素收得率的标准化残差也成正态分布，同样通过线性回归得到表5。

图5 锰元素回归标准化残差直方图

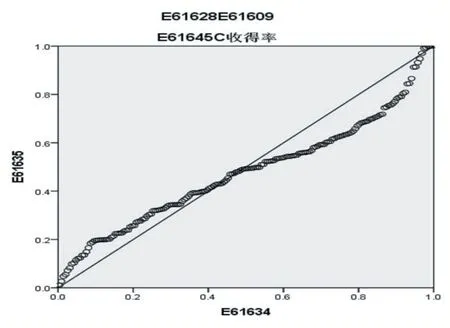
图6 锰元素回归标准正态图

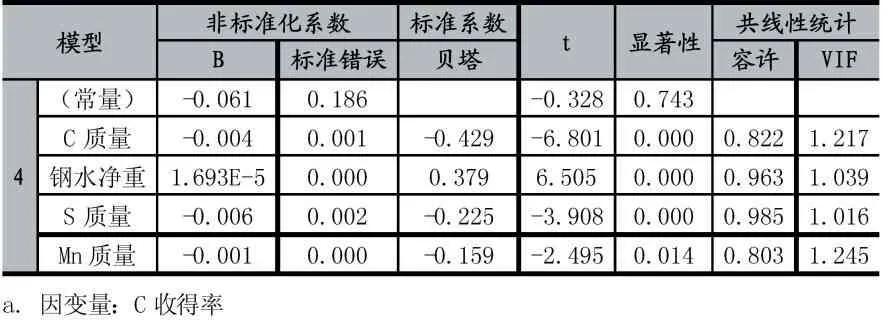
表5 Mn 元素收得率预测值的回归系数表

通过表中的数据，各因素的显著性都小于0.1，故认为其拟合的显著性较大，于是有：

同样，对该方程进行数值验算，代入五组数据进行求解得到其相对误差表如表6。

表6 Mn 元素收得率预测方程的相对误差表（线性回归）

得其相对误差在7.02%以内，则预测结果相对准确。

（3）BP 神经网络模型

尽管采用线性回归可以用来预测其元素历史收得率，但是仅考虑了线性情况，存在一定的局限性，我们希望能够有更好的方法提高预测的准确度。神经网络具有自学习、自组织、较好的容错性和优良的非线性逼近能力。在该题中，具有多种主要因素影响因素，即有多种输入。因此可以采用BP 神经网络的方法进一步改进模型和算法，通过将原始数据划分成训练集和验证集，从而预测元素的历史收得率。

用一个数学表达式进行抽象与概括，得到神经元的数学模型：

为了预测C 和Mn 的收得率，我们利用BP 神经网络算法对原始数据进行处理，将原数据分为训练集和验证集。将C、Mn 两种合金元素收得率的预测值与实际值进行比较，做出对比图，如图7 和图8 所示。

图7 碳的收得率学习和测试对比图

图8 锰的收得率学习和测试对比图

最后，得到的C 和Mn 元素的预测收得率以及相应的相对误差如表7、表8 所示。

表7 碳元素的收得率预测结果的相对误差表（BP 神经网络）

表8 锰元素的收得率预测结果的相对误差表（BP 神经网络）

相对于线性回归而言而言，采用神经网络的学习方法更加的精准，其中C 元素收得率预测的相对误差均小于6.21%，Mn 元素收得率预测的相对误差均小于3.67%，预测更加有效。

2.3 问题3的分析与求解

由于不同合金料的价格不同，则不同的选择也会带来不同的收益以及不同的钢材合格率，根据《常用合金料成分说明》中的数据，可以得知：

在满足以上成本条件的同时还要满足下列合金元素含量的国家标准，以HRB400B 为例，如表9 所示。

表9 合金元素含量的国家标准表

针对问题2 多元线性规划所得的拟合方程，可以通过钢水净重、转炉终点的含量求出表8 中五种元素的连铸正样值：

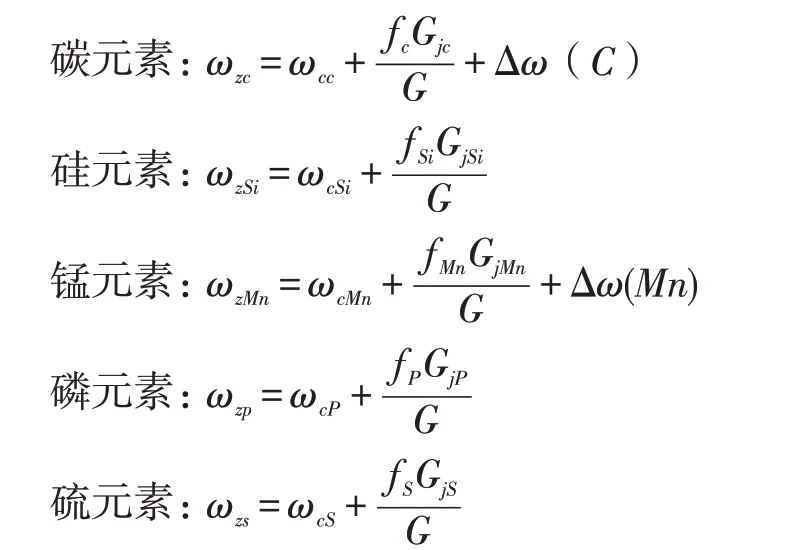
根据国家标准标可知，各合金元素的含量范围在其内控区间内，由此可以得到五个控制因素，从《炼钢历史数据》中任选几组数据，对其进行线性规划，可以得到下式：

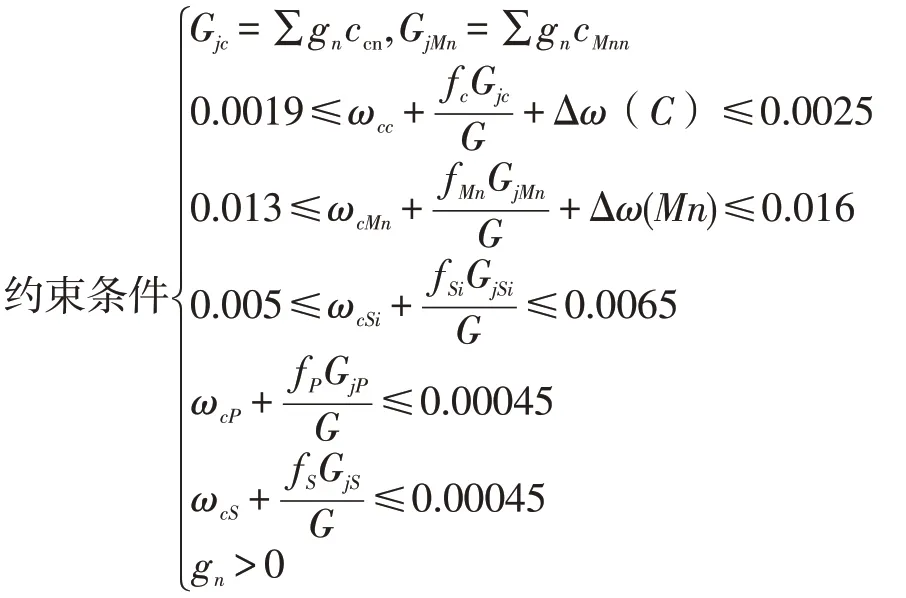
构建一个数学规划模型，求满足条件下的q 的最小值，求解得到下列结果，如表10 所示。

表10 合金配料表

增加硅锰面和石油焦增碳剂的使用，可以分别提高碳和锰元素的吸收量，使得其达到内控区间的要求，与此同时，这两种材料的价格相对而言较低，由计算可知，总的花费在12306.28 元，优化钢材质量的同时减小了炼钢成本。

3 配料方案优化总结与建议

通过详细的分析，我们诚挚地提出以下四点优化总结与建议：

（1）提高转炉终点C、Mn、Si、S、P 在钢水中的含量；

（2）增加温度来提高转炉终点时C、Mn、Si、S、P 在钢水中的吸收率；

（3）提高脱氧合金化的反应时长，来提高C 元素的收得率；

（4）提高使用硅锰面和石油焦增碳剂的比重来降低经济成本。