基于混合优化RBF 神经网络的月平均气温预测

魏爽，王丽吉，吴书成，鲁奕岑

（浙江省气象信息网络中心,杭州310017）

0 引言

随着全球气温的升高，气候变化已经引起人们的普遍关注。由于影响气温变化的机制和因素十分复杂，长期气温预报主要依靠的统计预报方法对复杂变化过程的拟合有较大局限性，所以预测的准确率难以令人满意。人工神经网络模型结构灵活并具有模拟非线性关系的能力，因而在气象等领域有较广泛的应用。严绍瑾等人[1]利用神经网络BP 型多映射模式对月平均温度进行了预测，马学款等人[2]也利用BP（Back-Propagation）型神经网络对西藏中短期极端温度预测方法进行了研究。

近年来，气象预测研究中经常采用BP 型网络，由于其所用的梯度下降方法容易造成收敛速度慢和局部极小的不足，采用能逼近任意精度的RBF 神经网络作为预测模型，克服BP 网络函数值的不紧密性，使收敛速度大大加快，并尝试利用基于遗传操作的粒子群算法优化RBF 网络的关键参数，通过增加交叉、变异操作，扩大了粒子群的搜索范围，能够避免粒子群早熟现象。应用该方法对月平均温度进行预测实验，通过实验结果说明算法的有效性。

1 RBF神经网络

RBF 神经网络[3-4]是具有三层结构的前向型神经网络。考虑采用Gaussian 型径向基函数，对于给定输入向量x∈Rn×1，RBF 网络将其映射到输出向量y∈Rm×1，此时网络输出定义为：

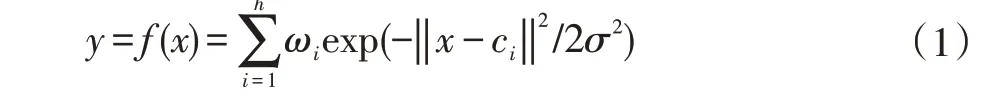
其中，ci为隐含层第i 个基函数的中心；‖·‖为欧氏范数；σ为函数的基宽度；wi为第i 个隐节点至输出的连接权值；h 为隐层单元数。

在径向基函数网络中，需要优化确定的关键参数[5]有两类：①基函数的中心ci和基宽度σ；②隐层与输出层间的连接权值wi。

2 基于遗传操作的PSO混合算法

2.1 基本PSO算法

粒子群算法[6]是一种基于种群搜索的自适应进化计算技术。其思想是受鸟类群体行为研究结果的启发，用组织社会行为代替了进化算法的自然选择机制，通过种群间个体协作来实现对问题最优解的搜索。

假设搜索空间为N 维，第i 个粒子在N 维空间的位置表示为xi=（xi1,xi2,…,xiN），飞行速度为vi=（vi1,vi2,…,viN），每个粒子都有一个由被优化目标函数决定的适应值（Fitness value），各个粒子记忆、追随当前的最优粒子，在解空间中搜索。每一次迭代中，粒子通过跟踪两个“极值”来更新自己：第一个是粒子自身搜索到的最优解，叫做个体极值点，用pbest表示；另一个是目前整个群体所发现的最优解，叫做全局极值点，用gbest表示。

每个粒子的速度和位置按式（2）、式（3）进行迭代修改：

其中，w 为惯性权重；r1、r2是均匀分布在[0,1]的两个随机数；c1、c2为学习因子；k 为迭代次数。

2.2 基于遗传操作的PSO算法

实际应用中，PSO 算法容易陷入局部最优点，导致得不到全局最优解。其原因是PSO 算法容易丧失种群多样性，致使群体中的大部分个体聚集在一个很小的范围内，从而失去了大范围搜索的能力。因此，在PSO算法的基础上结合遗传操作[7]，可以使种群多样性不致丧失过快或始终保持一定的多样性水平，当算法陷入局部最优时，使之能够跳出局部最优点，有利于算法的全局搜索，并且可以提高搜索精度。

现在设置遗传操作触发的条件为：当算法未达到总迭代次数M，若连续t 次迭代，得到的最优解都不改变，则认为算法陷入局部最优点，此时触发遗传操作，具体如下：

（1）选择：采用随机竞争选择方式[8]。先计算出适应度值，然后采用轮盘赌方法选出染色体对，通过染色体对之间的比较，选出高适应度值的个体进入交配池。

（2）交叉：根据染色体结构，采用算术交叉方法[8]，保证产生的子代均在可行区域内。假设X1和X2为要进行交叉父代个体，则交叉后的子代个体如式（4）。

其中r∈[0,1]。

（3）变异：采用均匀变异[9]，使搜索点可以在整个搜索空间内自由的移动，从而增加种群多样性。假设个体X=x1x2…xk…xl，xk为变异点，取值范围为新个体为X=x1x2…xk'…xl，则新基因值如式（5），其中r'∈[0,1]的一个随机数。

（4）交叉和变异概率的选择：为了防止算法不能收敛或收敛过程过长，应设定交叉概率随着迭代次数逐渐变小，最后趋于某一稳定值，同时使变异概率逐渐变大，防止个体出现未成熟收敛的情况。所以采用基于捕食搜索策略[10]的遗传算法，使交叉概率pc和变异概率pm随着进化代数动态改变。

其中，k 为迭代次数，M 为总迭代次数，pcmax、pcmin分别为最大、最小交叉概率；pmmax、pmmin分别为最大、最小变异概率。

3 基于PSO-GA混合优化的RBF算法

传统的RBF 网络学习算法[11]对RBF 参数的设置是基于参数空间局部信息的，不是参数空间的全局最优。为获得具有最优结构的RBF 网络，提出一种基于PSO-GA 混合优化的RBF 网络算法。

3.1 算法思想

首先确定神经网络的结构：输入层为n 个输入，隐层单元数为h，输出层为m 个神经元。对粒子群的位置向量xi进行实数编码，一个编码代表一个可行解，分别按行展开，结构如式（7）。

然后利用PSO-GA 混合算法搜索最优位置，适应度函数采用平均绝对误差（Mean Absolute Error，MAE）公式加上1 的倒数，即：

其中，N 为训练样本总数，yi为理想输出值，yi'为实际输出值。适应度函数值越大，表示预测效果越好。表1 给出了实验初始化参数。

表1 初始化参数表

3.2 算法步骤

（1）初始化参数。给定粒子群规模S，隐层单元数h，迭代计数器t 和总迭代次数M。

（2）初始化粒子群。设定学习因子c1，c2，惯性权重w，随机产生规模为S 的粒子群和每个粒子的初始速度vi，对每个粒子位置采用式（7）结构进行编码。

（3）用式（2）和式（3）对每个粒子的速度和位置进行更新，产生下一代粒子群。

（4）对每个粒子，根据式（8）求出每个粒子适应度值，并更新当前个体极值pbest和全局极值gbest。

（5）检查是否陷入局部最优，若陷入则触发遗传操作，否则转向步骤（6）。

（6）判断是否达到总迭代次数，若是则输出最优粒子位置编码。否则转向步骤（3）。

（7）用梯度下降法进一步修正最优粒子编码，再将得到的基函数的中心ci、基宽度σ和输出层与隐层间的连接权值wi代入RBF 网络中，得到月平均气温预测序列。

算法流程图如图1 所示。

图1 基于PSO-GA混合优化RBF神经网络流程图

4 预测应用

为验证混合算法在预测应用中的性能，选用浙江省杭州站1985～2018 年月平均气温资料，以1985～2014 年30 年的数据作为训练数据，用以预测2015～2017 年的月平均气温，并利用平均绝对百分比误差（MAPE）和均方误差（RMSE）2 个统计指标将预测值与实况值进行比较，以分析预测的准确程度。

4.1 输入时滞的确定

将多年月平均温度看成是一个离散的时间序列y（t），认为每一时间点的数据值与此前n 个时间值有关（n 称为时延或时滞），即有一函数F，使时间序列y（t）满足

为了确定参数n 的值，以30 年的训练数据为基础，初步限定时延窗口在3～7 的范围内，进行重复迭代训练得到平均绝对误差MAE，如表2 所示。其中，最小的平均绝对误差是1.12，因此选取时延n=6，即以过去的6 个值来预测当前值。

表2 不同输入参数得到的MAE 值

4.2 预测效果的检验和对比分析

将样本按前述划分方法分为训练集和测试集，得到2015～2017 年各月平均气温预测值，并与标准的RBF 网络和BP 网络同期对应的预测结果进行比较，将月尺度的预测值按时间顺序连成一条曲线，由图2 可见，混合优化RBF 网络模型预测结果比传统神经网络对实况温度拟合效果更好，预测的温度变化趋势和相位与实际情况更一致。

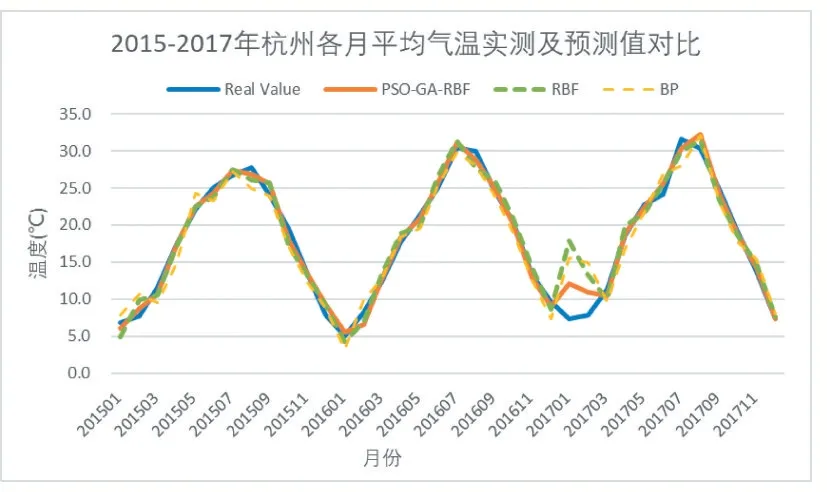
图2 2015～2017年各月平均气温实测及预测值对比

计算三种网络模型对2015～2017 年3 年月平均温度预测的统计指标值（表3）。可见，混合优化的RBF网络模型各种误差整体上比传统的RBF 和BP 网络模型相应的误差值更小。表明混合优化的RBF 网络模型对南京站月平均气温的拟合预测效果是理想的。

为了检验基于PSO-GA 混合优化的RBF 网络模型的预测能力和稳定性，对2018 年1～12 月进行了逐月平均气温预测。如图3。三种模型都比较成功的预测了2018 年月平均温度的变化趋势，同样进行误差分析，如表4 所示。混合优化的RBF 网络模型预测的各种误差仍然很小，平均绝对误差比传统的RBF 和BP网络模型分别小了6.44%和7.65%，均方误差同样小了0.64℃和1.03℃。

表3 2015～2017 年三种模型月平均气温预测指数对比

为了检验基于PSO-GA 混合优化的RBF 网络模型的预测能力和稳定性，对2018 年1～12 月进行了逐月平均气温预测。如图3。三种模型都比较成功的预测了2018 年月平均温度的变化趋势，同样进行误差分析，如表4 所示。混合优化的RBF 网络模型预测的各种误差仍然很小，平均绝对误差比传统的RBF 和BP网络模型分别小了6.44%和7.65%，均方误差同样小了0.64℃和1.03℃。

图3 2018年1～12月各月平均气温预测值与实测值对比

最后，对浙江省温州、奉化、丽水3 个站点2018 年1～12 月月平均气温利用上述方法建模，如表5 所示。结果同样表明，混合优化的RBF 网络模型在预测精度上仍优于标准的RBF 和BP 网络模型，具有普遍的适用性。

表4 2018 年1～12 月三种模型预测值及预测指数对比

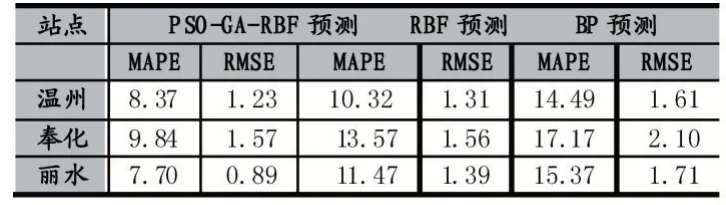
表5 2018 年1～12 月三种模型预测指数对比

5 结语

为解决传统的RBF 网络学习算法对关键参数的设置基于空间局部信息的不足这一问题，提出一种基于遗传操作的粒子群混合优化的RBF 网络预测算法，通过增加选择、交叉和变异操作，融合PSO 与GA 两者的优势，从而避免了PSO 早熟现象。实验证明，与传统的RBF 和BP 网络模型相比，混合优化的RBF 网络模型预测的温度变化趋势和相位与实际情况更一致，具有预报精度高，预测能力稳定等特点，可以为短期气候预测提供借鉴和参考。