2019年北京卷理科第18题别解与推广

(邮编：271400)

山东省泰安市宁阳第一中学

试题已知抛物线C:x2=-2py经过点(2,-1).

(Ⅰ)求抛物线C的方程及其准线方程；

(Ⅱ)设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M、N，直线y=-1分别交直线OM、ON于点A、B，求证：以AB为直径的圆经过y轴上的两个定点.

这是2019年北京卷理科第18题，我们首先给出试题的一种新解法.

解答(Ⅰ) 由抛物线C:x2=-2py经过点(2,-1)，则4=2p，所以抛物线C的方程为x2=-4y，其准线方程为y=1；

设以线段AB为直径的圆与y轴上的两个交点为P、Q，由圆的性质得|PF|=|QF|.由圆中相交弦定理得|PF|·|QF|=|AF|·|BF|=|xA|·|xB|=|xA·xB|=4，则|PF|=|QF|=2，故以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).

一般地，对于抛物线C:x2=-2py(p>0)，我们有如下结论：

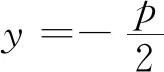
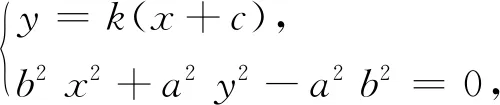
则y1y2=k2[x1x2+c(x1+x2)+c2]

(x1+a)(x2+a)=x1x2+a(x1+x2)+a2

若将命题2中左焦点改为右焦点，直线x=-c改为x=c，我们有如下结论：

若将命题2中直线x=-c改为x=c，我们有如下结论：

若将命题2中左焦点改为右焦点，我们有如下结论：

可以仿照命题2的证明给出命题3、4、5的证明，从略.

y1y2=k2[x1x2+c(x1+x2)+c2]

(x1+a)(x2+a)

可以仿照命题6的证明给出命题7、8、9的证明，从略.