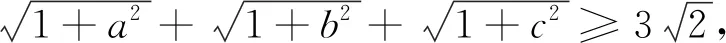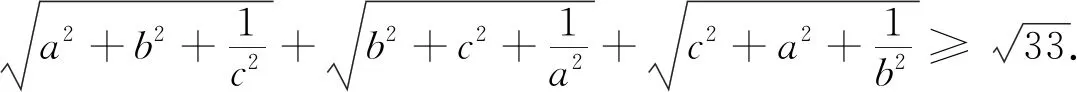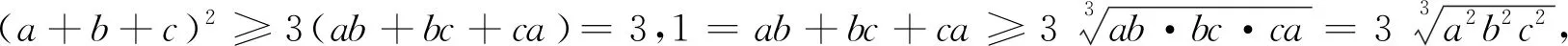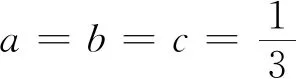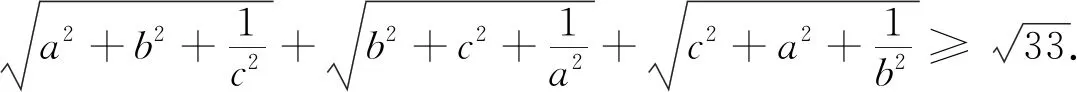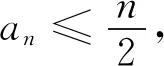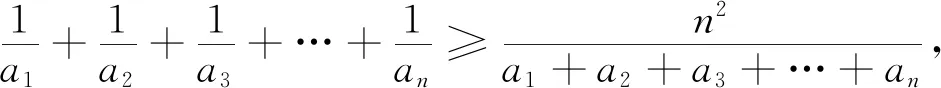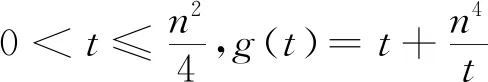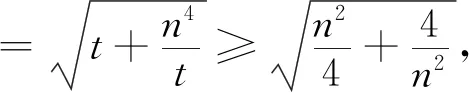活跃在不等式试题中的闵可夫斯基不等式

(邮编：430074)

武汉职业技术学院商学院

本文选取各类试题中的不等式问题，巧妙地运用闵可夫斯基不等式来秒杀，笔者给出如下几例应用说明，希望给大家带来帮助.

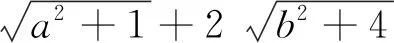
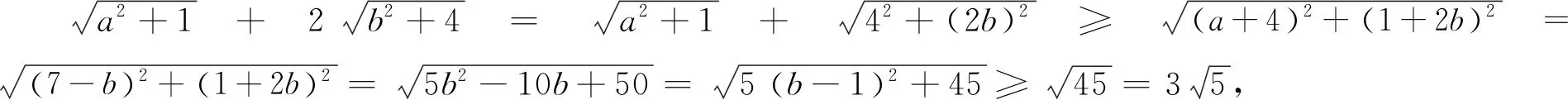
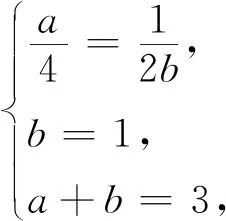
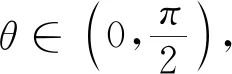
解由闵可夫斯基不等式可得

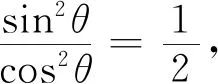
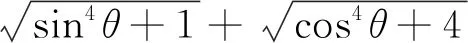
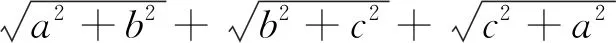
解由闵可夫斯基不等式可得

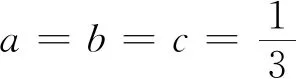
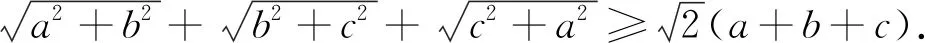
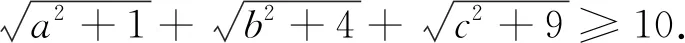
此题在文[1]的证法从取等号条件入手确定λ值，巧用柯西不等式求证，运用闵可夫斯基不等式可以秒杀文[1]中的问题.

证明由闵可夫斯基不等式可得

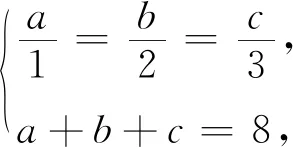
解由闵可夫斯基不等式可得

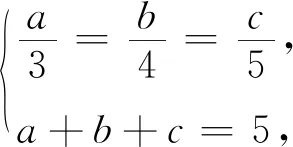
由上述问题联想2018年重庆数学夏令营试题第一试压轴题如下

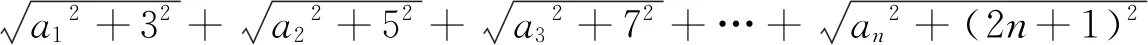
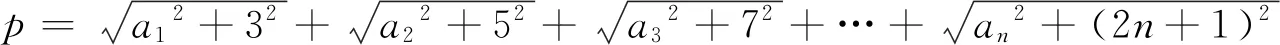
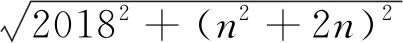
即20182+(n2+2n)2=m2，则[m-(n2+2n)][m+(n2+2n)]=20182=(2×1009)2.

由n2+2n-m与n2+2n+m奇偶性相同，且1009为质数，可得

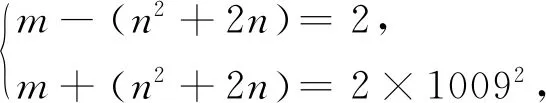
例4 (安振平先生博客问题4922)设a、b∈R+，且ab=a+b.

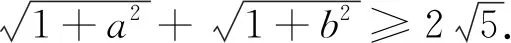
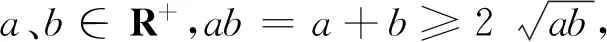
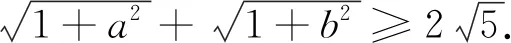
类似问题(安振平先生博客问题4921)设a、b、c∈R+且ab+bc+ca=a+b+c.

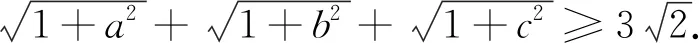
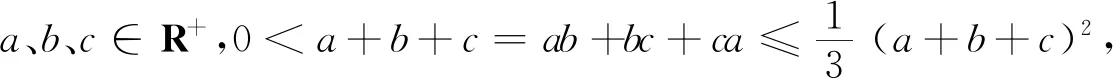
由闵可夫斯基不等式可得